当前位置：首页 > news >正文

Disjoint 集合数据结构或 Union-Find 算法简介

news 2025/8/1 23:15:41

联合查找算法是一种对此类数据结构执行两个有用操作的算法：

查找：确定特定元素在哪个子集中。这可用于确定两个元素是否在同一子集中。
联合：将两个子集连接成一个子集。这里首先我们必须检查这两个子集是否属于同一个集合。如果否，则我们无法执行联合。

不相交集的 UNION 和 FIND 操作

一组元素 a1、a2、…an 上的关系可以分为等价类。元素 a 的等价类是 S 的子集，它包含 S 中与 a 相关的所有元素。

通过这两个操作将一组元素划分为等价的类

1.联合

2. 寻找

一个集合被分成子集。每个子集都包含相关元素。如果我们知道 ai 和 aj 这两个元素是相关的，那么我们可以执行以下操作：

1.找到子集：包含ai的Si

2.找到子集：包含aj的Sj

3.如果S,和Si是两个独立的子集

然后我们通过合并 Si 和 Sj 创建一个新的子集

新子集 = Si C ∪ PS j 。

该算法是动态的，因为在算法过程中，集合可以通过并集操作改变。

例子：

让我们检查一个例子来理解数据结构是如何应用的。为此，请考虑以下问题陈述

问题：给定一个无向图，任务是检查图中是否包含循环。

例子：

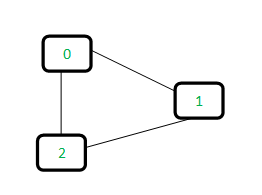
输入：下图

输出：是
解释：存在顶点 {0, 1, 2} 的循环。

我们已经讨论了一种在有向图中检测循环的算法。这里可以使用 Union-Find 算法来检查无向图是否包含循环。这个想法是，

最初创建仅包含一个节点的子集，该节点是其自身的父节点。现在在遍历边时，如果边的两个端节点属于同一个集合，则它们形成一个循环。否则，执行 union 将子集合并在一起。

注意：此方法假定图形不包含任何自环。

插图：

请按照下图更好地理解

让我们考虑下图：

使用数组来跟踪子集以及哪些节点属于该子集。让数组成为parent[]。

最初，父数组的所有槽都被初始化为保存与节点相同的值。

父母 [] = {0, 1, 2}。同样，当节点的值与其父节点的值相同时，即为该节点子集的根。

现在一条一条地处理所有的边。
Edge 0-1:
=> 找到顶点0和1所在的子集。
=> 0 和 1 属于子集 0 和 1。
=> 因为它们在不同的子集中，所以取它们的并集。
=> 要合并，请将节点 0 作为节点 1 的父节点，反之亦然。
=> 1 成为 0 的父级（1 现在代表子集 {0, 1}）
=> parent[] = {1, 1, 2}

边 1-2：
=> 1 在子集 1 中，2 在子集 2 中。
=> 因为它们在不同的子集中，所以取并集。
=> 将 2 作为 1 的父级。（2 现在代表子集 {0, 1, 2}）
=> parent[] = {1, 2, 2}

边 0-2：
=> 0 在子集 2 中，2 也在子集 2 中。
=> 因为 1 是 0 的父级，而 2 是 1 的父级。所以 0 也属于子集 2
=> 因此，包括这条边形成一个循环。

因此，上图包含一个循环。

按照以下步骤来实现这个想法：

最初创建一个parent[]数组来跟踪子集。
遍历所有边：
- 通过查找 parent[] 数组检查每个节点属于哪个子集，直到节点和父节点相同。
- 如果两个节点属于同一个子集，则它们属于一个循环。
- 否则，对这两个子集执行联合操作。
如果没有找到循环，则返回 false。

下面是上述方法的实现。

// A union-find algorithm to detect cycle in a graph
#include <bits/stdc++.h>
using namespace std;// a structure to represent an edge in graph
class Edge {
public:int src, dest;
};// a structure to represent a graph
class Graph {
public:// V-> Number of vertices, E-> Number of edgesint V, E;// graph is represented as an array of edgesEdge* edge;
};// Creates a graph with V vertices and E edges
Graph* createGraph(int V, int E)
{Graph* graph = new Graph();graph->V = V;graph->E = E;graph->edge = new Edge[graph->E * sizeof(Edge)];return graph;
}// A utility function to find the subset of an element i
int find(int parent[], int i)
{if (parent[i] == i)return i;return find(parent, parent[i]);
}// A utility function to do union of two subsets
void Union(int parent[], int x, int y) { parent[x] = y; }// The main function to check whether a given graph contains
// cycle or not
int isCycle(Graph* graph)
{// Allocate memory for creating V subsetsint* parent = new int[graph->V];// Initialize all subsets as single element setsfor(int i = 0; i < graph->V; i++) {parent[i] = i;}// Iterate through all edges of graph, find subset of// both vertices of every edge, if both subsets are// same, then there is cycle in graph.for (int i = 0; i < graph->E; ++i) {int x = find(parent, graph->edge[i].src);int y = find(parent, graph->edge[i].dest);if (x == y)return 1;Union(parent, x, y);}return 0;
}// Driver code
int main()
{/* Let us create the following graph0| \| \1---2 */int V = 3, E = 3;Graph* graph = createGraph(V, E);// add edge 0-1graph->edge[0].src = 0;graph->edge[0].dest = 1;// add edge 1-2graph->edge[1].src = 1;graph->edge[1].dest = 2;// add edge 0-2graph->edge[2].src = 0;graph->edge[2].dest = 2;if (isCycle(graph))cout << "Graph contains cycle";elsecout << "Graph doesn't contain cycle";return 0;
}// This code is contributed by rathbhupendra

输出