堆(数据结构系列11)
目录
前言:
1.优先级队列概念
2.堆的概念
3.堆的存储方式
4.堆的创建
5.创建堆的时间复杂度
6.堆的插入和删除
6.1堆的插入
6.2堆的删除
结束语:
前言:
上一次博客中小编主要与大家分享了 二叉树一些相关的知识点和一些练习题,下面继续跟着小编一起来学习堆的知识吧!本次博客中小编会主要分享一些堆的基础知识。
1.优先级队列概念
首先我们先来认识一下什么是优先级队列,我们在前面的博客中提到了队列是一种先进先出的数据结构,但是在有些情况下,操作的数据可能会带有优先级,一般出队列的时候可能会需要优先级高的元素先出队列,那么显然我们的队列是无法做到的,那么在这种情况下,数据结构应该提供两个最基本的操作,一个是返回最高优先级对象,一个是添加新的对象,这种数据结构就是优先级队列。
2.堆的概念
如果有一个关键码的集合K = {k0, k1, k2, ..., kn - 1},把他的所有元素按完全二叉树的顺序存储方式存储在一个一维数组中,并满足:ki <= k2i + 2且ki <= k2i + 2(ki >= k2i + 1 且 ki >= k2i + 2) i = 0,1,2,...,则称为小堆(或者是大堆)。将根结点最大的堆叫做最大堆或大跟堆,根结点最小的堆叫最小堆或小根堆。
如下图所示:
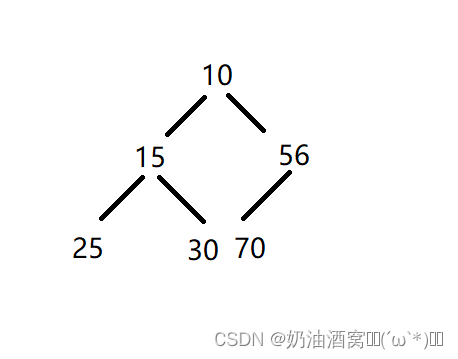

堆的性质:
- 堆中某个结点的值总是不大于或不小于其父结点的值。
- 堆总是一颗完全二叉树。
3.堆的存储方式
从堆的概念我们知道堆是一颗完全二叉树,因此可以层序的规则采用顺序的方式来高效存储。
注意:
对于非完全二叉树,则不适合使用顺序方式进行存储,因此为了能够还原二叉树,空间中必须要存储空结点,就会导致空间利用率比较低。
将元素存储到数组中后,可以根据二叉树章节的性质对树进行还原,假设i为结点在数组中的下标,则有:
如果i为0,则i表示的结点为根节点,否则i结点的双亲结点为(i - 1)/ 2。
如果2 * i + 1小于结点个数,则结点i的左孩子下标为2 * i + 1,否则没有左孩子。
如果2 * i + 2小于结点个数,则结点i的右孩子下标为2 * i + 2,否则没有右孩子。

如上图所示:其中结点的个数为6,那么对于下标为5的结点来说它的父亲结点就是(5 - 1)/ 2。
对于下标为2的结点来说,由于(2 * 2) + 1 < 6,所以她的左孩子就是(2 * 2)+ 1,由于(2 * 2)+ 2 > 6 ,故它没有右孩子。
4.堆的创建
堆的创建是由向下调整来完成的,那么什么是向下调整呢?
向下调整:
我们直接以创建一颗大跟堆来举个例子。

这颗二叉树我们应该怎么用向上调整的方式来进行调整为一颗大跟堆或者是小根堆呢?
首先我们下调整都是从二叉树的最后一个结点开始调整的如下图所示:
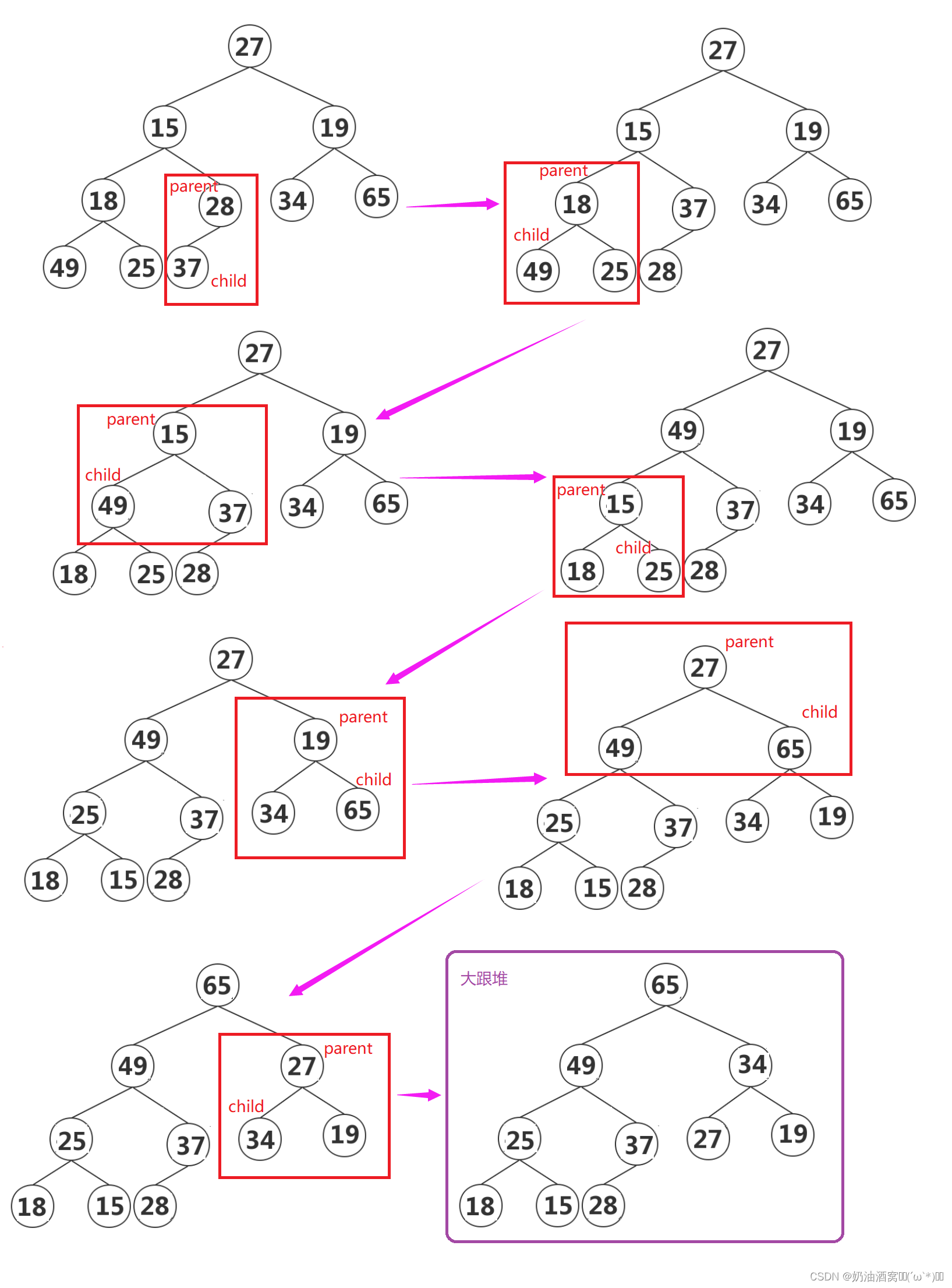
步骤:
1.让parent标记需要调整的结点,child标记parent的左孩子(注意:parent如果有孩子一定先是有左孩子)。
2.如果parent的左孩子存在,即:child < size ,进以下操作,直到parent的左孩子不存在。
- parent右孩子是否存在,如果存在那么找到左右孩子中最大的孩子。
- 让parent与child进行比较,如果parent大于较大的孩子child,调整结束,否则:交换parent与较大的孩子child,交换完之后,parent中小的元素向下移动,可能导致子树不满足对的性质,因此需要继续向下调整,即parent = child,child = parent * 2 + 1;然后继续2。
注意:
在调整以parent为根的二叉树时,必须要满足parent的左子树和右子树已经是堆了才可以向下调整。
代码实现:
核心代码:
package 堆;public class Heap {public int[] elem;public int usedSize;public Heap() {this.elem = new int[10];}//初始化堆public void initElem(int[] array) {for (int i = 0; i < array.length; i++) {elem[i] = array[i];usedSize++;}}//创建堆public void createHeap() {//从最后一个结点所对应的父亲结点开始调整//由于最后一个结点的下标值为usedSize - 1,故parent的下标值就是最后一个结点的下标值 - 1再除以2。//即:parent = (usedSize - 1 - 1) / 2//直到调整到parent = 0为止。for (int parent = (usedSize - 1 - 1) / 2; parent >= 0; parent--) {shiftDown(parent,usedSize);}}//向下调整public void shiftDown(int parent, int len) {//知道parent所在的位置之后就先确定要调整的child的结点的位置,首先要调整就是左孩子结点int child = 2 * parent + 1;//至少要有一个左孩子,否则的话就不做调整。while (child < len) {//判断是否存在右孩子,并且右孩子结点大于左孩子结点的值//将child++,保证child指向的左右孩子的最大的那一个if (child + 1 < len && elem[child] < elem[child + 1]) {child++;}//判断最大孩子结点的值与父亲结点的值的大小//如果child所在的位置的值比parent所在位置的值大就将两者互换if (child + 1 < len && elem[child] < elem[child + 1]) {child++;}//判断最大孩子结点的值与父亲结点的值的大小//如果child所在的位置的值比parent所在位置的值大就将两者互换if (elem[child] > elem[parent]) {//互换int tmp = elem[child];elem[child] = elem[parent];elem[parent] = tmp;//换完之后在继续向下调整//让parent指向孩子结点的位置//child指向现在parent所在位置的左孩子结点//继续重复上述的循环,直到不满足条件就说明这课树就已经调整完毕了parent = child;child = parent * 2 + 1;}else {break;}}}
}
测试代码:
package 堆;public class Test {public static void main(String[] args) {Heap heap = new Heap();int[] array = {27,15,19,18,28,34,65,49,25,37};heap.initElem(array);heap.createHeap();}
}
结果展示:
创建小根堆和上述代码差不多,只是在比较parent 和child的大小部分与其不同,大家可以下来自己实现一下。
5.创建堆的时间复杂度
为了简化我们此处使用满二叉树来给大家证明一下。
如下所示:

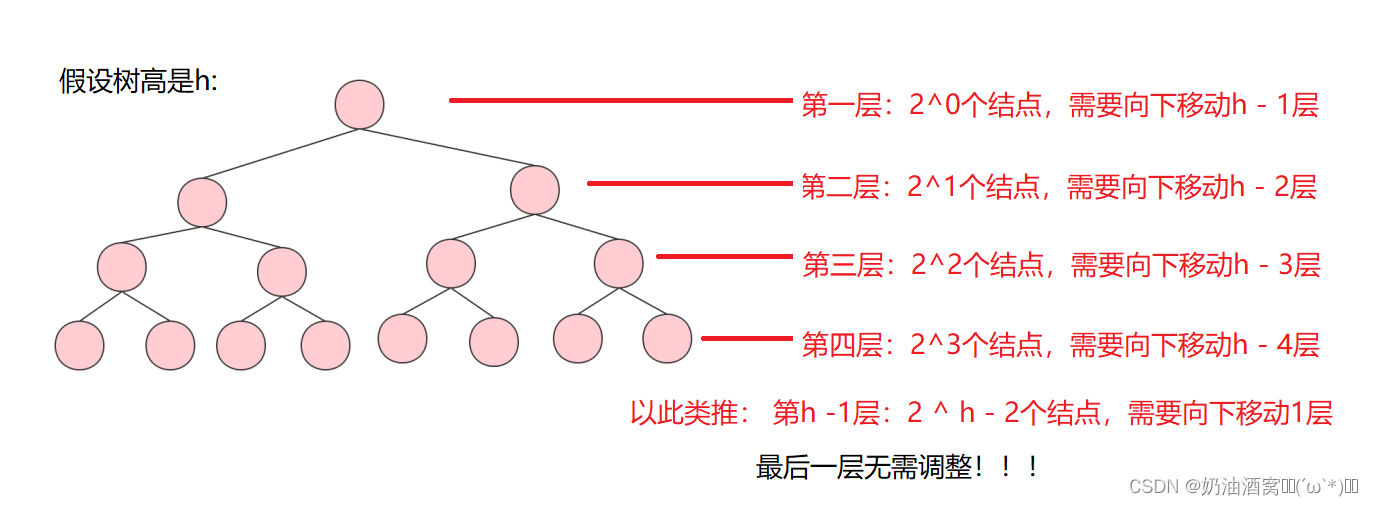
推理如下所示:
6.堆的插入和删除
6.1堆的插入
堆的插入需要两步:
- 先将元素放入到底层空间中(注意:空间不够需要扩容)
- 将最后新插入的结点向上调整,直到满足堆的性质。
向上调整:向上调整就是我们直接拿这个结点和根结点进行比较即可。
示意图如下所示,以大跟堆为例:
核心代码入所示:
//插入一个元素public void offer(int val) {//判满if (isFull()) {//扩容elem = Arrays.copyOf(elem,2 * elem.length);}//将新元素放置在最后一个位置上elem[usedSize++] = val;//向上调整shiftUp(usedSize - 1);}private void shiftUp(int child) {int parent = (child - 1) / 2;while (child > 0) {if (elem[child] > elem[parent]) {//交换int tmp = elem[child];elem[child] = elem[parent];elem[parent] = tmp;//重新赋值child = parent;parent = (child - 1) / 2;}else {break;}}}public boolean isFull() {return usedSize == elem.length;}
结果展示:

6.2堆的删除
堆的删除一定是删除堆顶元素,具体步骤入下:
- 将堆顶元素与堆中的最后一个元素互换。
- 将堆中有效数据减一
- 对堆顶元素进行向下调整
核心代码如下所示:
//删除堆顶元素public void pop() {//1.将堆顶元素与最后一个元素互换int tmp = elem[0];elem[0] = elem[usedSize - 1];elem[usedSize - 1] = tmp;//2.有效长度减一usedSize--;//3.将堆顶元素向下调整shiftDown(elem[0],usedSize);}结果展示: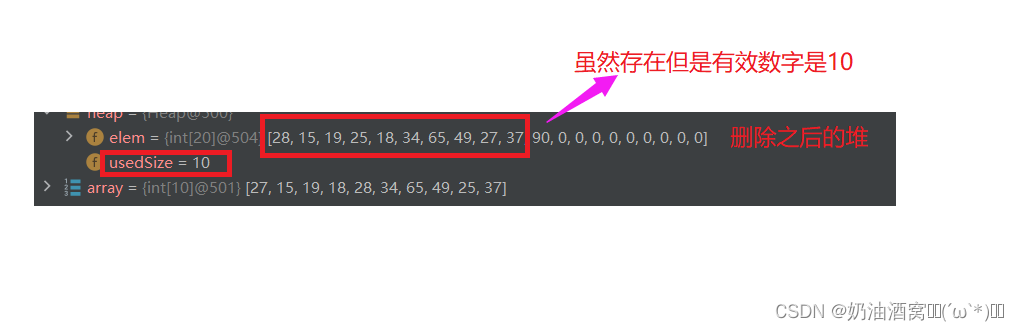
结束语:
好啦这节有关于堆的基本知识点小编就与大家分享到这里啦!如果想要继续深入了解的同学继续跟着小编一起走吧!下一次小编将会和大家继续分享一些有关于堆的知识的,希望对大家有所帮助,想要学习的同学记得关注小编和小编一起学习吧!如果文章中有任何错误也欢迎各位大佬及时为小编指点迷津(在此小编先谢过各位大佬啦!)
