106. 从中序与后序遍历序列构造二叉树
文章目录
- 106. 从中序与后序遍历序列构造二叉树
- 思路
- 105. 从前序与中序遍历序列构造二叉树
- 思路
- 思考
106. 从中序与后序遍历序列构造二叉树
106. 从中序与后序遍历序列构造二叉树
给定两个整数数组 inorder 和postorder,其中 inorder 是二叉树的中序遍历, postorder 是同一棵树的后序遍历,请你构造并返回这颗 二叉树 。
示例 1:

输入:inorder = [9,3,15,20,7], postorder = [9,15,7,20,3]
输出:[3,9,20,null,null,15,7]
示例 2:
输入:inorder = [-1], postorder = [-1]
输出:[-1]
提示:
- 1 <= inorder.length <= 3000
- postorder.length == inorder.length
- -3000 <= inorder[i], postorder[i] <= 3000
- inorder 和 postorder 都由 不同 的值组成
- postorder 中每一个值都在 inorder 中
- inorder 保证是树的中序遍历
- postorder 保证是树的后序遍历
思路
首先回忆一下如何根据两个顺序构造一个唯一的二叉树,相信理论知识大家应该都清楚,就是以 后序数组的最后一个元素为切割点,先切中序数组,然后根据中序数组,反过来再切后序数组。一层一层切下去,每次后序数组最后一个元素就是节点元素。
如果让我们肉眼看两个序列,画一棵二叉树的话,应该分分钟都可以画出来。
流程如图:

那么代码应该怎么写呢?
说到一层一层切割,就应该想到了递归。
来看一下一共分几步:
-
第一步:如果数组大小为零的话,说明是空节点了。
-
第二步:如果不为空,那么取后序数组最后一个元素作为节点元素。
-
第三步:找到后序数组最后一个元素在中序数组的位置,作为切割点
-
第四步:切割中序数组,切成中序左数组和中序右数组 (顺序别搞反了,一定是先切中序数组)
-
第五步:切割后序数组,切成后序左数组和后序右数组
-
第六步:递归处理左区间和右区间
不难写出如下代码:(先把框架写出来)
注意:以下代码中ir,il,pr,pl 分别表示中序和后序数组的左右区间,左闭右开
// 第一步
if ir - il == 0 {return nil }if ir - il == 1 {return &TreeNode{Val:postorder[pr-1]}}// 第二步:后序遍历数组最后一个元素,就是当前的中间节点val := postorder[pr - 1]curTreeNode := &TreeNode{Val:val}// 第三步:找切割点idx := 0for i := il;i < ir;i++ {if inorder[i] == val {idx = ibreak}}// 第四步:切割中序数组,得到 中序左数组和中序右数组// 第五步:切割后序数组,得到 后序左数组和后序右数组// 第六步 递归构造左右子树,拼接为当前节点的左右子树curTreeNode.Left = dfs(inorder,il,idx,postorder,pl,pl + idx - il)curTreeNode.Right = dfs(inorder,idx+1,ir,postorder,pl + idx - il,pr-1)return curTreeNode
难点大家应该发现了,就是如何切割,以及边界值找不好很容易乱套。
此时应该注意确定切割的标准,是左闭右开,还有左开右闭,还是左闭右闭,这个就是不变量,要在递归中保持这个不变量。即从最入口的时候是左闭右开,则递归的过程中要一直遵循这个原则,这样区间才不会乱套。
在切割的过程中会产生四个区间,把握不好不变量的话,一会左闭右开,一会左闭右闭,必然乱套!
首先要切割中序数组,为什么先切割中序数组呢?
切割点在后序数组的最后一个元素,就是用这个元素来切割中序数组的,所以必须要先切割中序数组。
中序数组相对比较好切,找到切割点(后序数组的最后一个元素)在中序数组的位置,然后切割,如下代码中我坚持左闭右开的原则:
假设找到切割点在中序数组中的索引为idx,则中序数组切割后,左数组是[il,idx),即起点还是il,但是右边界是到idx,且不包含idx,因为idx是当前节点的数值,不可能出现在子树中的,这样[il,idx)符合了我们坚持的左闭右开原则。而中序数组的右边界则是[idx+1,ir),同样排除了idx,即当前递归层取出了中序数组中idx对应的数值构造了一个树节点。
curTreeNode.Left = dfs(inorder,il,idx,postorder,pl,pl + idx - il)
curTreeNode.Right = dfs(inorder,idx+1,ir,postorder,pl + idx - il,pr-1)
接下来就看看怎么切割后序数组。
首先后序数组的最后一个元素指定不能要了,这是切割点 也是 当前二叉树中间节点的元素,已经用了。
后序数组的切割点怎么找?
后序数组没有明确的切割元素来进行左右切割,不像中序数组有明确的切割点,切割点左右分开就可以了。
此时有一个很重的点,就是中序数组大小一定是和后序数组的大小相同的(这是必然)。
中序数组我们都切成了左中序数组和右中序数组了,那么后序数组就可以按照左中序数组的大小来切割,切成左后序数组和右后序数组。
因为左中序数组的元素个数为 idx - il个,所以左后序数组的元素也应该是 idx - il个,从而推断出左后序数组的区间为[pl,pl + idx - il) ,有个方便记忆的方法,中序左数组元素个数为idx - il,左后序数组的元素个数也是右区间减去左区间的,所有就是(pl + idx - il ) - pl = idx - il,即左后续数组的终止位置是 需要加上 中序区间的大小,而右后序区间则应该从pl + idx - il直到倒数第二个元素。
完整代码如下:
/*** Definition for a binary tree node.* type TreeNode struct {* Val int* Left *TreeNode* Right *TreeNode* }*/
func buildTree(inorder []int, postorder []int) *TreeNode {// 后序最后一个节点一定是根节点,找到根节点后,可以切割中序的左右子树,并切割后续的左右子树// 而后递归构造左右子树即可if len(postorder) == 0 {return nil}root := dfs(inorder,0,len(inorder),postorder,0,len(postorder))return root
}func dfs(inorder []int,il ,ir int,postorder []int,pl,pr int) *TreeNode {if ir - il == 0 {return nil }if ir - il == 1 {return &TreeNode{Val:postorder[pr-1]}}val := postorder[pr - 1]curTreeNode := &TreeNode{Val:val}idx := 0for i := il;i < ir;i++ {if inorder[i] == val {idx = ibreak}}curTreeNode.Left = dfs(inorder,il,idx,postorder,pl,pl + idx - il)curTreeNode.Right = dfs(inorder,idx+1,ir,postorder,pl + idx - il,pr-1)return curTreeNode
}

105. 从前序与中序遍历序列构造二叉树
105. 从前序与中序遍历序列构造二叉树
给定两个整数数组preorder和inorder,其中preorder是二叉树的先序遍历, inorder 是同一棵树的中序遍历,请构造二叉树并返回其根节点。
示例 1:
输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
输出: [3,9,20,null,null,15,7]
示例 2:
输入: preorder = [-1], inorder = [-1]
输出: [-1]
提示:
- 1 <= preorder.length <= 3000
- inorder.length == preorder.length
- -3000 <= preorder[i], inorder[i] <= 3000
- preorder 和 inorder 均 无重复 元素
- inorder 均出现在 preorder
- preorder 保证 为二叉树的前序遍历序列
- inorder 保证 为二叉树的中序遍历序列
思路
思路上上面106题一模一样,所以直接上代码吧!!
Go代码
/*** Definition for a binary tree node.* type TreeNode struct {* Val int* Left *TreeNode* Right *TreeNode* }*/
func buildTree(preorder []int, inorder []int) *TreeNode {if len(preorder) == 0 {return nil}root := dfs(preorder,0,len(preorder),inorder,0,len(inorder))return root
}func dfs(preorder []int,pl,pr int,inorder []int,il,ir int) *TreeNode {if pr - pl == 0 {return nil}if pr - pl == 1 {return &TreeNode{Val:preorder[pl]}}val := preorder[pl]curTreeNode := &TreeNode{Val:val}var idx intfor i,num := range inorder {if num == val {idx = ibreak}}// 中序的切割容易,前序的切割则遵循长度和中序一致就比较容易确定了,如左中序变为il,idx,则长度是idx - il// 左前序的起点是pl+1无疑,区间长度需要是idx-il,从而确定左前序右边界为pl + 1 + idx - ilcurTreeNode.Left = dfs(preorder,pl + 1,pl + 1 + idx - il,inorder,il,idx)curTreeNode.Right = dfs(preorder,pl + 1 + idx - il ,pr,inorder,idx + 1,ir)return curTreeNode
}

思考
前序和中序可以唯一确定一棵二叉树。
后序和中序可以唯一确定一棵二叉树。
那么前序和后序可不可以唯一确定一棵二叉树呢?
前序和后序不能唯一确定一棵二叉树!,因为没有中序遍历无法确定左右部分,也就是无法分割。
举一个例子:
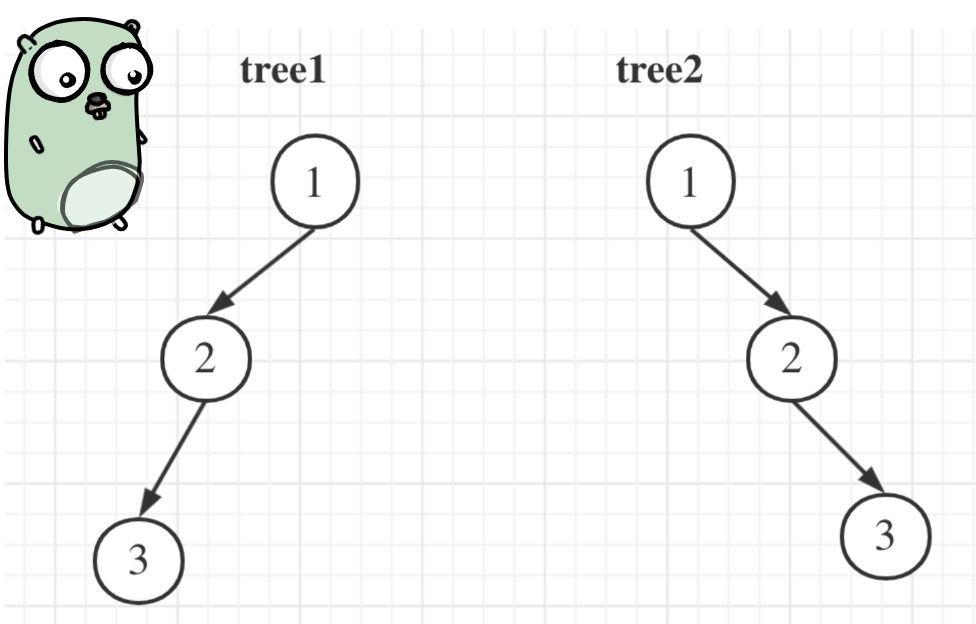
tree1 的前序遍历是[1 2 3], 后序遍历是[3 2 1]。
tree2 的前序遍历是[1 2 3], 后序遍历是[3 2 1]。
那么tree1 和tree2的前序和后序完全相同,这是一棵树么,很明显是两棵树!
所以前序和后序不能唯一确定一棵二叉树!
