GAMES101(10节,几何)
Geometry
implicit隐式几何表示:
函数f(x,y,z):
根据函数fn描述几何,遍历所有空间内 的点,如果带入xyz到函数f(x,y,z)结果=0那就绘制这个点
如果xyz求值结果>0表示在几何外,=0在表面,<0在几何内
构造几何csg( constructive solid geometry):
建立bool运算(这被应用到建模软件中)
并集
交集 \ 差集:通过建立基本几何形体,利用bool创建复杂几何
距离函数:
距离函数:任何点到几何表面的最近距离,
如果点在外面,函数结果为正,如果在内部,距离为负
比如当两个球逐渐靠近,会发生融合,这是对距离函数sdf做混合,用于渲染平滑的几何形状
比如:水滴融合
explicit显示几何表示:
直接表示(不会改变):
point clouds点云:
几何由密集的点表示
Polygon / triangle meshes
由多边形网格表示:obj文件存储所有顶点数据的信息,和索引顺序
参数表示(输入参数,得到转换后的结果):
参数映射方式:
遍历所有的UV坐标通过映射函数f(u,v) ,投影到空间中的某一点
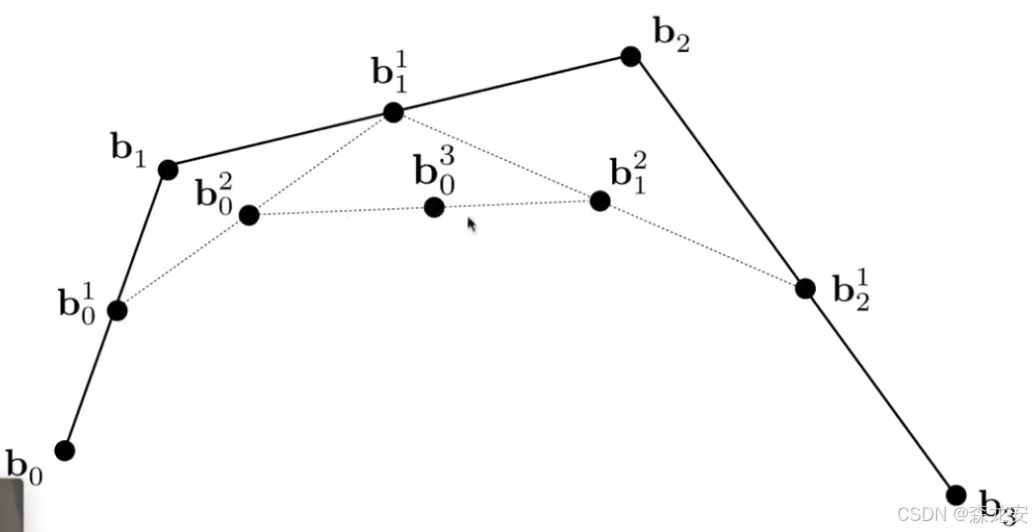
bezier surfaces贝塞尔曲线
用一系列控制点定义曲线,每个点相连形成连线
从所有连线取相同时间t(参数),再次相连,直到仅剩一个点为止,这个点作为曲线上的某一个点
重复上述,直到从每个线段取完所有可能t
细分曲面
NURBS样条曲线
作业四
题目:
绘制Bézier 曲线,其中bezier函数负责绘制 Bézier 曲线,提供控制点序列,每次使t增加微小值,并调用recursive_bezier函数,负责返回 Bézier 曲线上对应点的坐标
