Dijkstra 算法
Dijkstra 算法( 迪杰斯特拉算法), 又叫最短路径算法, 这是常见的图论中的最短路径算法, 由 Edsger W.Dijkstra 在 1959 年发表。 这种算法能够给定一个图中的源节点( Source Node), 寻找该节点到所有其他节点的最短路径。 结合无人车路由的 lane point 场景, 算法可以这样描述:
Dijkstra 算法采用的是一种贪心的策略, 声明一个数组 dis 来保存源点到各个顶点的最短距离和一个保存已经找到了最短路径的顶点的集合: T, 初始时,原点 s 的路径权重被赋为 0 ( dis[s] = 0)。 若对于顶点 s 存在能直接到达的边( s,m), 则把 dis[m]设为 w( s, m) ,同时把所有其他顶点的路径长度设为无穷大。 初始时, 集合 T 只有顶点 s。
然后, 从 dis 数组选择最小值, 则该值就是源点 s 到该值对应的顶点的最短路径, 并且把该点加入到 T 中, OK, 此时完成一个顶点,
然后, 我们需要看看新加入的顶点是否可以到达其他顶点并且看看通过该顶点到达其他点的路径长度是否比源点直接到达短, 如果是, 那么就替换这些顶点在 dis 中的值。
然后, 又从 dis 中找出最小值, 重复上述动作, 直到 T 中包含了图的所有顶点。
下面我求下图, 从顶点 v1 到其他各个顶点的最短路径。
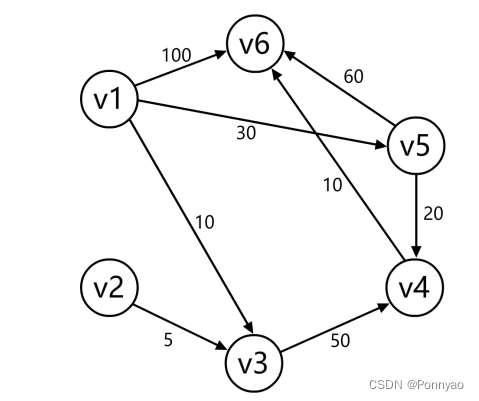
首先第一步, 我们先声明一个 dis 数组, 该数组初始化的值为:

我们的顶点集 T 的初始化为: T={v1}
既然是求 v1 顶点到其余各个顶点的最短路程, 那就先找一个离 1 号顶点最近的顶点。 通过数组 dis 可知当前离 v1 顶点最近是 v3 顶点。 当选择了 2 号顶点后, dis[2](下标从 0 开始) 的值就已经从“估计值” 变为了“确定值”,即 v1 顶点到 v3 顶点的最短路程就是当前 dis[2]值。 将 V3 加入到 T 中。
为什么呢? 因为目前离 v1 顶点最近的是 v3 顶点, 并且这个图所有的边都是正数, 那么肯定不可能通过第三个顶点中转, 使得 v1 顶点到 v3 顶点的路程进一步缩短了。 因为 v1 顶点到其它顶点的路程肯定没有 v1 到 v3 顶点短.
既然确定了一个顶点的最短路径, 下面我们就要根据这个新入的顶点 V3 会有出度, 发现以 v3 为弧尾的有: < v3,v4 >,那么我们看看路径: v1– v3– v4的长度是否比 v1– v4 短, 其实这个已经是很明显的了, 因为 dis[3]代表的就是v1– v4 的长度为无穷大, 而 v1– v3– v4 的长度为: 10+50=60, 所以更新 dis[3]的值,得到如下结果:

因此 dis[3]要更新为 60。 这个过程有个专业术语叫做“松弛”。 v1 顶点到v4 顶点的路程即 dis[3], 通过 < v3,v4> 这条边松弛成功。 这便是 Dijkstra 算法的主要思想: 通过“边” 来松弛 v1 顶点到其余各个顶点的路程。然后, 我们又从除 dis[2]和 dis[0]外的其他值中寻找最小值, 发现 dis[4]的值最小, 通过之前是解释的原理, 可以知道 v1 到 v5 的最短距离就是 dis[4]的值,
然后, 我们把 v5 加入到集合 T 中, 然后, 考虑 v5 的出度是否会影响我们的数组 dis 的值, v5 有两条出度: < v5,v4>和 < v5,v6>,然后我们发现: v1–v5– v4 的长度为: 50, 而 dis[3]的值为 60, 所以我们要更新 dis[3]的值.另外,v1-v5-v6 的长度为: 90, 而 dis[5]为 100, 所以我们需要更新 dis[5]的值。 更新后的 dis 数组如下图:

然后, 继续从 dis 中选择未确定的顶点的值中选择一个最小的值, 发现 dis[3]的值是最小的, 所以把 v4 加入到集合 T 中, 此时集合 T={v1,v3,v5,v4},然后,考虑 v4 的出度是否会影响我们的数组 dis 的值, v4 有一条出度: < v4,v6>,然后我们发现: v1– v5– v4– v6 的长度为: 60, 而 dis[5]的值为 90, 所以我们要更新 dis[5]的值, 更新后的 dis 数组如下图:

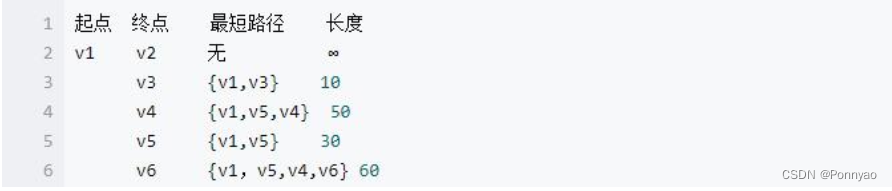
然后, 我们使用同样原理, 分别确定了 v6 和 v2 的最短路径, 最后 dis 的数组的值如下:

因此, 从图中, 我们可以发现 v1-v2 的值为: ∞, 代表没有路径从 v1 到达v2。 所以我们得到的最后的结果为: