【蓝桥杯-筑基篇】搜索
🍓系列专栏:蓝桥杯
🍉个人主页:个人主页
目录
递归树
1.递归构建二进制串
2.全排列的 DFS 解法
3.全排列的 BFS 解法
4.数的划分法
5.图书推荐
递归树
递归树是一种用于分析递归算法时间复杂度的工具。它可以将递归算法的执行过程可视化,从而更好地理解算法的时间复杂度。
递归树的构造方法如下:
- 首先,将递归算法的输入规模表示为根节点。
- 然后,将递归算法的每一次递归调用表示为树的一个子节点。
- 对于每个子节点,将其表示为一个与父节点相同的问题,但是规模更小的子问题。
- 重复上述步骤,直到递归算法的规模为 1 或者 0。
递归树的叶子节点表示递归算法的基本操作,而递归树的深度表示递归算法的递归深度。通过递归树,可以很容易地计算出递归算法的时间复杂度。
以下是一个递归树的例子:
构建二进制串
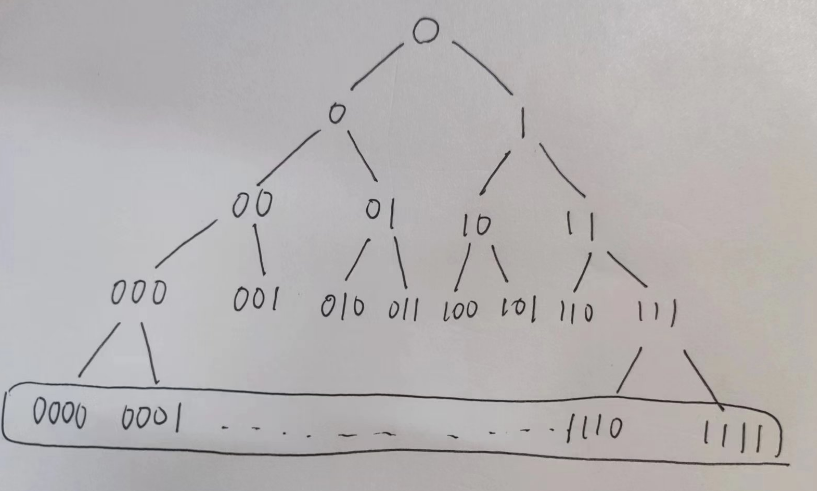
这个递归树表示的是一个将一个大小为 n 的问题分成两个大小为 n/2 的子问题的递归算法。从根节点到叶子节点的路径长度为 O(log n),因此,这个递归算法的时间复杂度为 O(n log n)。在实际应用中,递归树常常用于分析递归。
1.递归构建二进制串
public class A {public static void main(String[] args) {dg(0,"");}private static void dg(int depth, String bin) {if(depth==4) {System.out.println(bin);return ;}dg(depth+1,bin+"0");dg(depth+1,bin+"1");}}0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111 修改一下:
public class A {public static void main(String[] args) {DFS(0,"");}private static void DFS(int depth, String bin) {if(depth==4) {System.out.println(bin);return ;}for (int i = 0; i <= 1; i++) {DFS(depth+1,bin+i);}}}优化:用数组存
在这个例子中,我们使用了一个静态数组arr来存储每个深度的值,当深度达到4时,我们输出这个数组。在DFS函数中,我们使用了一个for循环来遍历每个深度的可能性,即0或1,然后将其存储在数组中,并递归调用DFS函数,直到深度达到4。
public class A {public static int[] arr=new int[4];public static void main(String[] args) {DFS(0);}private static void DFS(int depth) {if(depth==4) {System.out.println(Arrays.toString(arr));return ;}for (int i = 0; i <= 1; i++) {arr[depth]=i;DFS(depth+1);}}}结果:
[0, 0, 0, 0] [0, 0, 0, 1] [0, 0, 1, 0] [0, 0, 1, 1]
[0, 1, 0, 0] [0, 1, 0, 1] [0, 1, 1, 0] [0, 1, 1, 1]
[1, 0, 0, 0] [1, 0, 0, 1] [1, 0, 1, 0] [1, 0, 1, 1]
[1, 1, 0, 0] [1, 1, 0, 1] [1, 1, 1, 0] [1, 1, 1, 1] 2.全排列的 DFS 解法
这段代码是一个全排列的DFS解法。我们使用了递归的方式来生成所有可能的排列。初始时,我们调用DFS函数,初始深度为0,初始答案为空字符串,n为3。在DFS函数中,我们首先判断当前深度是否达到n,如果达到,则输出答案并返回。否则,我们遍历所有可能的下一位数,如果该数未被使用,则将其加入到答案中,并递归调用DFS函数,深度加1。当递归返回时,我们将该数从答案中删除,以便遍历其他可能的下一位数。下面是代码实现:
public class A {public static void main(String[] args) {DFS(0,"",3);}private static void DFS(int depth, String ans,int n) {if(depth==n) {System.out.println(ans);return ;}for (int i = 1; i <= n; i++) {if(!ans.contains(""+i))DFS(depth+1,ans+i,n);}}}123 132 213 231 312 321 3.全排列的 BFS 解法
这段代码是一个全排列的BFS解法。我们使用了一个队列来存储每个深度的可能性,初始时,队列中包含了所有可能的第一位数。然后,我们遍历队列中的所有元素,将当前深度的可能性加入到队列中。当深度达到n时,队列中的所有元素即为所有可能的排列。
下面是代码实现:
public class A {public static void main(String[] args) {int n=3;Queue<String> q=new LinkedList<String>();//将所有可能的第一位数加入队列中for (int i = 1; i <= n; i++) q.offer(""+i);while(!q.isEmpty()) {String head=q.poll();for (int i = 1; i <= n; i++) {//如果当前深度的可能性中已经包含了i,则跳过if(head.contains(""+i)) continue;String son=head+i;//如果当前深度为n,则输出当前深度的可能性if(son.length()==n) System.out.println(son);//否则将当前深度的可能性加入到队列中else q.offer(son);}}}}123 132 213 231 312 321 4.数的划分法
问题描述
将整数n分成k份,且每份不能为空,任意两份不能相同(不考虑顺序)。
例如:n=7,k=3,下面三种分法被认为是相同的:
1,1,5;1,5,1;
5,1,1;
问有多少种不同的分法。输入格式
n,k
输出格式
一个整数,即不同的分法
样例输入
7 3
样例输出
4 {四种分法为:1,1,5;1,2,4;1,3,3;2,2,3;}
给定一个正整数n,将其拆分成k个正整数的和,求方案数。这里使用了深度优先搜索的方法,从min开始枚举每个数,递归求解。其中,fanan表示当前的方案,ans表示方案数,cnt表示调用次数。
public class A {public static int cnt;//调用次数public static int ans;//方案数public static void main(String[] args) {int n=7;//给定的正整数int k=3;//将其拆分成k个正整数的和dfs(n,k,1,"");//从1开始枚举每个数System.out.println("方案数:"+ans);//输出方案数System.out.println("调用次数:"+cnt);//输出调用次数}/*** 深度优先搜索* @param n 给定的正整数* @param k 将其拆分成k个正整数的和* @param min 枚举的最小值* @param fanan 当前的方案*/private static void dfs(int n, int k, int min, String fanan) {cnt++;//调用次数加1if(k==1 && min<=n) {//如果k=1且min<=nans++;//方案数加1System.out.println(fanan+n);//输出方案return ;}if(min*k>n) return ; //剪枝for (int i = min; i < n; i++) {//枚举每个数idfs(n-i,k-1,i,fanan+i+"+");//递归搜索}}}
1+1+5
1+2+4
1+3+3
2+2+3
方案数:4
调用次数:15
5.图书推荐
你是否发现,购物、短视频、资讯等平台背后的智能推荐算法,不断分析着你的购物偏好和浏览习惯;价格算法时刻计算调整着你能购买到的商品价位;导航算法、网约车平台算法和无人驾驶汽车算法等等,时刻影响着我们的出行……
无论是否愿意,我们的生活已被算法包围。为了帮助大家全面认知我们当前所身处的世界,消弭技术发展过快带来的困扰与隐忧,《人人都离不开的算法——图解算法应用》一方面从人工智能算法的五大核心应用领域—公共、商业、医疗、工业、金融的典型场景出发,以通俗化、故事化和漫画化的具体事例,深入解读算法是如何在各行各业具体发挥作用和对日常生活的影响;另一方面,将从算法的责任监管和立法治理等角度,阐述算法开发与应用者们应该如何守好伦理底线,让科技向善而行。
《人人都离不开的算法——图解算法应用》脉络清晰,图文并茂,无论你是工作中会接触到算法应用的从业人员,还是对算法应用感到好奇的小白,本书都有助于你打开视野,看到算法在实际应用中的波澜壮阔。

