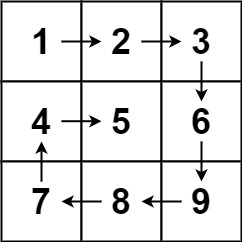
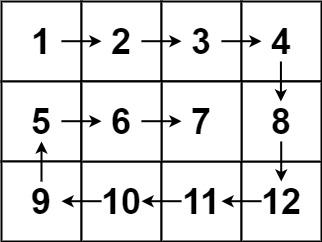
力扣第五十四题——螺旋矩阵
内容介绍
给你一个
m行n列的矩阵matrix,请按照 顺时针螺旋顺序 ,返回矩阵中的所有元素。示例 1:
输入:matrix = [[1,2,3],[4,5,6],[7,8,9]] 输出:[1,2,3,6,9,8,7,4,5]示例 2:
输入:matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]] 输出:[1,2,3,4,8,12,11,10,9,5,6,7]提示:
m == matrix.lengthn == matrix[i].length1 <= m, n <= 10-100 <= matrix[i][j] <= 100
完整代码
int directions[4][2] = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};int* spiralOrder(int** matrix, int matrixSize, int* matrixColSize, int* returnSize) {if (matrixSize == 0 || matrixColSize[0] == 0) {*returnSize = 0;return NULL;}int rows = matrixSize, columns = matrixColSize[0];int visited[rows][columns];memset(visited, 0, sizeof(visited));int total = rows * columns;int* order = malloc(sizeof(int) * total);*returnSize = total;int row = 0, column = 0;int directionIndex = 0;for (int i = 0; i < total; i++) {order[i] = matrix[row][column];visited[row][column] = true;int nextRow = row + directions[directionIndex][0], nextColumn = column + directions[directionIndex][1];if (nextRow < 0 || nextRow >= rows || nextColumn < 0 || nextColumn >= columns || visited[nextRow][nextColumn]) {directionIndex = (directionIndex + 1) % 4;}row += directions[directionIndex][0];column += directions[directionIndex][1];}return order;
}
思路详解
一、问题背景
给定一个二维数组,要求按照螺旋顺序遍历数组,并返回一个一维数组,其中包含按螺旋顺序遍历得到的元素。
二、解题思路
-
边界处理:
- 首先检查数组是否为空,如果为空,则直接返回空数组。
-
初始化:
- 创建一个二维数组
visited,用于标记数组中已经遍历过的元素。 - 初始化数组的大小为行数乘以列数。
- 创建一个一维数组
order,用于存储按螺旋顺序遍历得到的元素。
- 创建一个二维数组
-
遍历策略:
- 定义一个方向数组
directions,包含四个方向:上、右、下、左。 - 初始化起点
row和column,以及方向索引directionIndex。 - 遍历数组,按照螺旋顺序填充
order数组。 - 在遍历过程中,如果下一个位置越界或者已经遍历过,则改变方向。
- 定义一个方向数组
-
结果返回:
- 遍历完成后,返回
order数组。
- 遍历完成后,返回
三、代码详解
- 边界处理:
- 如果数组为空,直接返回空数组。
if (matrixSize == 0 || matrixColSize[0] == 0) {*returnSize = 0;return NULL;
}
- 初始化:
- 创建
visited数组并初始化为0。 - 创建
order数组并分配内存。 - 初始化
rows、columns、total和directionIndex。
- 创建
int rows = matrixSize, columns = matrixColSize[0];
int visited[rows][columns];
memset(visited, 0, sizeof(visited));
int total = rows * columns;
int* order = malloc(sizeof(int) * total);
*returnSize = total;
- 遍历策略:
- 初始化起点
row和column,以及方向索引directionIndex。 - 遍历数组,按照螺旋顺序填充
order数组。 - 在遍历过程中,如果下一个位置越界或者已经遍历过,则改变方向。
- 初始化起点
int row = 0, column = 0;
int directionIndex = 0;
for (int i = 0; i < total; i++) {order[i] = matrix[row][column];visited[row][column] = true;int nextRow = row + directions[directionIndex][0], nextColumn = column + directions[directionIndex][1];if (nextRow < 0 || nextRow >= rows || nextColumn < 0 || nextColumn >= columns || visited[nextRow][nextColumn]) {directionIndex = (directionIndex + 1) % 4;}row += directions[directionIndex][0];column += directions[directionIndex][1];
}
- 结果返回:
- 遍历完成后,返回
order数组。
- 遍历完成后,返回
return order;
四、总结
通过上述步骤,我们能够有效地遍历二维数组并按照螺旋顺序返回一维数组。关键在于正确地初始化数组、遍历策略和结果返回。这种方法的时间复杂度为O(n),其中n为数组的大小。空间复杂度为O(n),用于存储一维数组和二维数组。
知识点精炼
一、核心概念
- 边界条件检查:在开始遍历之前,检查输入的二维数组是否为空。
- 二维数组访问:使用两个索引变量来访问二维数组中的元素。
- 动态数组分配:在内存中动态分配一维数组来存储遍历结果。
- 方向数组:使用一个二维数组来表示遍历的方向。
二、知识点精炼
-
初始化:
- 创建一个二维数组
visited来标记数组中已经遍历过的元素。 - 创建一个一维数组
order来存储按螺旋顺序遍历得到的元素。
- 创建一个二维数组
-
遍历策略:
- 初始化起点
row和column,以及方向索引directionIndex。 - 遍历数组,按照螺旋顺序填充
order数组。 - 在遍历过程中,如果下一个位置越界或者已经遍历过,则改变方向。
- 初始化起点
-
结果返回:
- 遍历完成后,返回
order数组。
- 遍历完成后,返回
三、性能分析
- 时间复杂度:O(n),其中n为数组的大小。
- 空间复杂度:O(n),用于存储一维数组和二维数组。
四、实际应用
- 数据处理:在处理二维数据时,这种算法可以帮助我们按照特定顺序访问数据。
- 算法竞赛:在算法竞赛中,掌握这种算法对于解决与二维数组遍历相关的问题非常有帮助。
五、代码实现要点
- 边界条件检查:确保输入的二维数组不为空。
- 动态数组分配:正确分配内存空间,避免内存泄漏。
- 遍历策略:正确实现螺旋遍历策略,避免数组越界和重复访问。
- 结果返回:正确返回遍历结果。
减少空间复杂度的思路
在原始代码中,我们使用了一个二维数组visited来标记已经遍历过的元素,这导致了较高的空间复杂度。为了减少空间复杂度,我们可以使用一个一维数组来替代二维数组,这样可以将空间复杂度从O(n)降低到O(1)。
以下是优化后的代码:
int* spiralOrder(int** matrix, int matrixSize, int* matrixColSize, int* returnSize) {if (matrixSize == 0 || matrixColSize[0] == 0) {*returnSize = 0;return NULL;}int rows = matrixSize, columns = matrixColSize[0];int* order = malloc(sizeof(int) * (rows * columns));*returnSize = rows * columns;int top = 0, bottom = rows - 1, left = 0, right = columns - 1;int index = 0;while (top <= bottom && left <= right) {// Traverse the top rowfor (int i = left; i <= right; i++) {order[index++] = matrix[top][i];}top++;// Traverse the rightmost columnfor (int i = top; i <= bottom; i++) {order[index++] = matrix[i][right];}right--;// If there is still a row leftif (top <= bottom) {// Traverse the bottom rowfor (int i = right; i >= left; i--) {order[index++] = matrix[bottom][i];}bottom--;}// If there is still a column leftif (left <= right) {// Traverse the leftmost columnfor (int i = bottom; i >= top; i--) {order[index++] = matrix[i][left];}left++;}}return order;
}
在这个优化版本中,我们使用了一个一维数组order来存储遍历结果,而不是使用一个二维数组visited来标记已经遍历过的元素。我们通过维护四个边界变量(top、bottom、left、right)来控制遍历的方向,并在每次迭代中只遍历尚未访问的部分。这种方法避免了使用额外的空间来存储已访问的元素,从而将空间复杂度降低到O(1)。