线性代数之行列式
一、思维导图
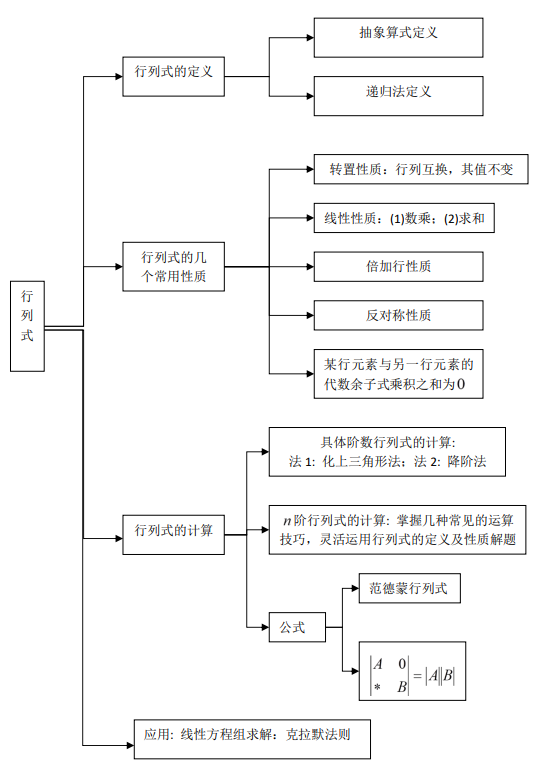
二、二阶、三阶行列式的定义
1、二阶行列式

2、三阶行列式
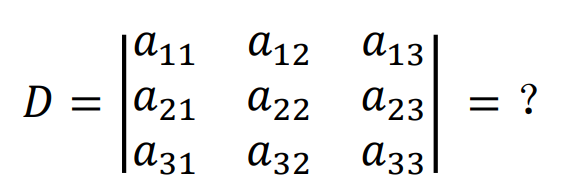
沙路法展开

3、解方程
3.1解二元一次方程组
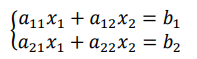
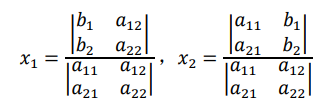
观察上面两个未知量的值不难发现,它 们的分母均是上述方程组未知量的系数形成的二阶行列式,𝑥1的分子是将系数行列 式的第一列换成了常数列其余列不变所得,𝑥2的分子是将系数行列式的第二列换 成了常数列其余列不变所得。我们将二阶行列式的这种定义法称为对角线法定义。
3.2 解三元线性方程组
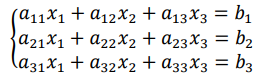

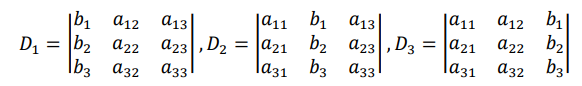
三、n阶行列式的定义
1、补充定义——排列的逆序数
• 𝒏级排列:由1, 2, … , 𝑛构成的有序数组称为一个𝒏级 排列。 • 排列的逆序:在一个排列中,如果一个较大的数 排在一个较小的数前面,则称它们构成一个逆序。
例1 在排列𝟐𝟏𝟓𝟑𝟒中,𝟐与𝟏、𝟓与𝟑、𝟓与𝟒均构成 逆序。
排列的逆序数:排列中逆序的总数称为逆序数。 注: 1. 排列 𝒋𝟏𝒋𝟐 ⋯ 𝒋𝒏 的逆序数记为: 𝛕(𝒋𝟏𝒋𝟐 ⋯ 𝒋𝒏) 2. 称逆序数为奇数的排列为奇排列,逆序数为偶 数的排列为偶排列
例:𝛕(𝟐𝟏𝟓𝟑𝟒)= 3
2、行列式的递归法定义
2.1元素的余子式、元素的代数余子式
第𝑖行第𝑗列元素𝑎𝑖𝑗的 余子式𝑀𝑖𝑗定义为去掉该元素所在的行去掉该元素所在的列,剩余元素按原来次 序排出的那个𝑛 − 1阶的行列式。
定义元素𝑎𝑖𝑗的代数余子式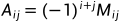 。
。
2.2 递归法定义
行列式的值=它某行元素与本行元素代数余子式的乘积之和



3、行列式的抽象算式定义法

即它的展开式为:每项由取自不同行不同列的𝑛个元素的乘积构成,每项前面的 符号由行标自然排列时列标排列的奇偶性决定。


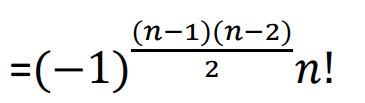
四、行列式常用的性质
性质 1 行列互换,其值不变。
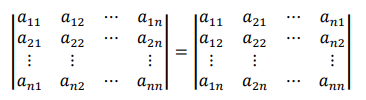
在行列式中,所有对行成立的结果,对列依 然成立。
例如下面性质 2 的描述结合性质 1 知,行列式中某列元素与其代数余 子式的乘积之和也等于此行列式的值。
性质 2 行列式中某行元素与其代数余子式的乘积之和等于此行列式的值
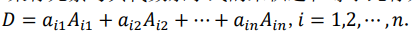
性质 3 (线性性质)
(1)数乘性质
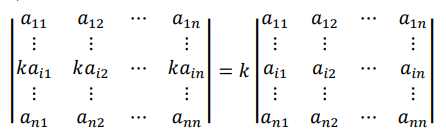
(2)求和性质

引理 若行列式中有两行元素对应相等,则其值为 0。
推论 若行列式中有两行元素对应成比例,则其值为 0。
性质 4 (倍加行性质)倍加行变换,其值不变。
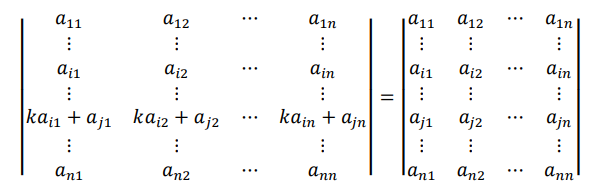
性质 5(反对称性质)两行对换,行列式的值反号
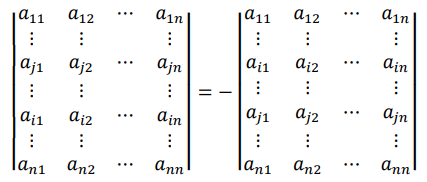
性质 6 行列式某一行的元素与另外一行元素代数余子式乘积之和为 0。
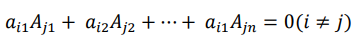
五、特殊的几个行列式
1、范德蒙行列式
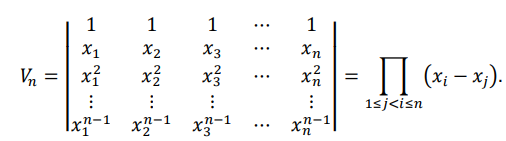

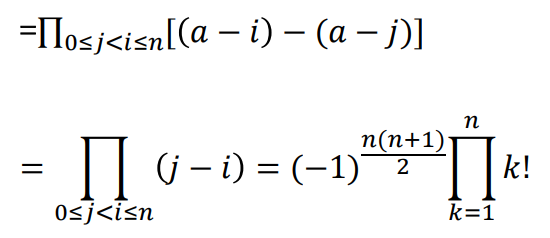
2、反对称行列式

证明:奇数阶反对称行列式的值为零。

3、几个结论


六、克莱默法则
1、定理:线性非齐次方程组
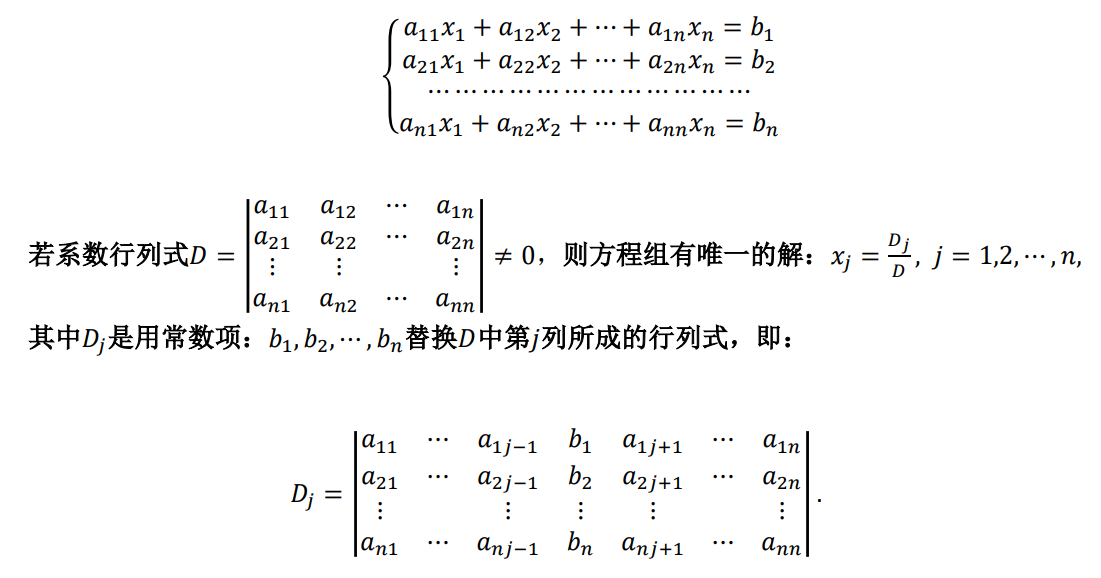
2、推论:齐次线性方程组


七、复习题

