518. 零钱兑换 II ——【Leetcode每日一题】
518. 零钱兑换 II
给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。
请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。
假设每一种面额的硬币有无限个。
题目数据保证结果符合 32 位带符号整数。
示例 1:
输入:amount = 5, coins = [1, 2, 5]
输出:4
解释:有四种方式可以凑成总金额:
5=5
5=2+2+1
5=2+1+1+1
5=1+1+1+1+1
示例 2:
输入:amount = 3, coins = [2]
输出:0
解释:只用面额 2 的硬币不能凑成总金额 3 。
示例 3:
输入:amount = 10, coins = [10]
输出:1
提示:
- 1 <= coins.length <= 300
- 1 <= coins[i] <= 5000
- coins 中的所有值 互不相同
- 0 <= amount <= 5000
思路:
此问题属于 0-1背包 的 完全背包 ,解法和 0-1背包类似:
0 - 1背包问题(万能统一代码)
定义一个二维数组dp 存储硬币组合数,其中 dp[i][j] 表示前 i 个硬币 可以凑成总金额 为 j 的 硬币组合数:
- 每种硬币的数量是无限的,所以可以重复使用
- 状态转移方程为:
dp[i][j]=dp[i−1][j]+dp[i][j−coins[i]]dp[i][j] = dp[i - 1][j] + dp[i][j - coins[i]]dp[i][j]=dp[i−1][j]+dp[i][j−coins[i]]
示例1 的dp二维数组为:
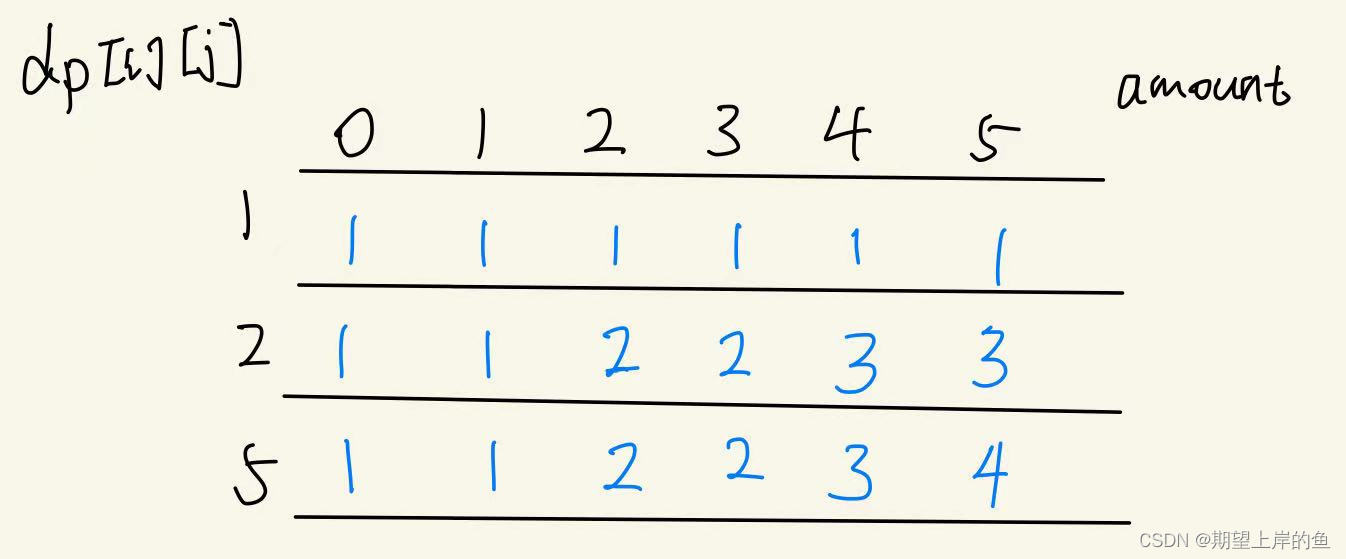
观察前 i 个硬币的状态仅与前 i -1 个硬币的状态有关,因此可以优化,将 dp 定义为一维数组,其中 dp[j] 既可以表示 dp[i-1][j] 也可以表示 dp[i ][j - coins[i]]:状态转移方程为:
dp[j]+=dp[j−coins[i]]dp[j] += dp[j - coins[i]]dp[j]+=dp[j−coins[i]]
代码:(Java)
public class Change {public static void main(String[] args) {// TODO Auto-generated method stubint[] coins = {1, 2, 5};int amount = 5;System.out.println(change(amount, coins));}public static int change(int amount, int[] coins) {int[] dp = new int[amount + 1];dp[0] = 1;for(int coin : coins) {for(int i = coin; i <= amount; i++) {dp[i] += dp[i - coin];}}return dp[amount];}
}
运行结果:

复杂度分析:
- 时间复杂度:O(len∗amount)O(len * amount)O(len∗amount), lenlenlen 为数组 coinscoinscoins 的长度,amountamountamount 为要凑成的总金额。
- 空间复杂度:O(amount)O(amount)O(amount) ,需要开辟一个一维数组 dp , 长度为amount+1amount + 1amount+1 ,amountamountamount 为要凑成的总金额。
322. 零钱兑换 I
注:仅供学习参考 如有不足,欢迎指正!
题目来源:力扣。
