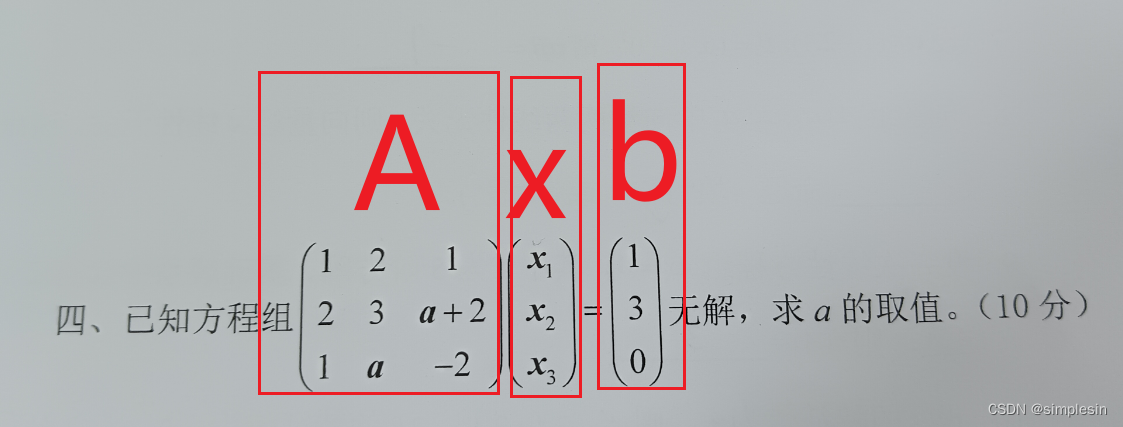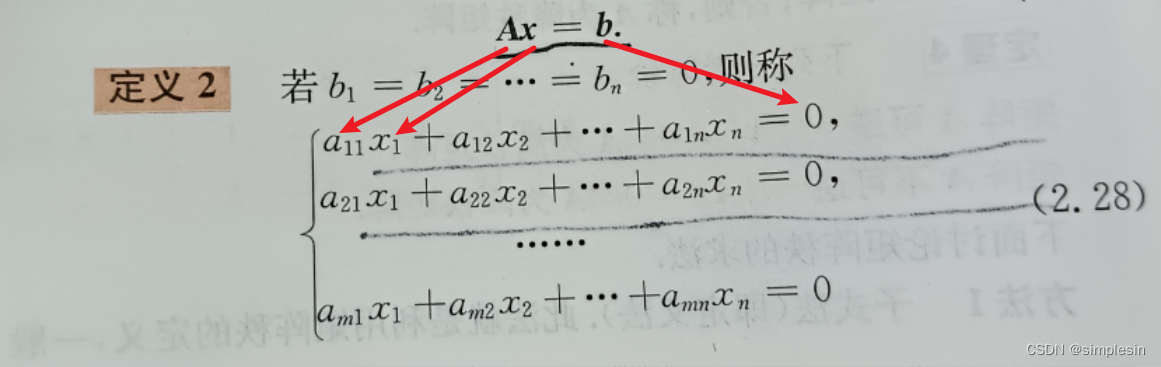线性代数知识点搜刮
求你别考太细...
目录
异乘变零定理
行列式转置 值不变
重要关系
中间相等,取两头
特征值公式
向量正交 = 点积为0
拉普拉斯定理
矩阵的秩
特征值和特征向量
|A|=特征值的乘积 & tr(A)=特征值的和
要记要背
增广矩阵
异乘变零定理
某行(列)元素与另一行(列)元素的代余子式乘积之和为0

3 * (-2) + 0 * 5 + 1 * 1 + 3 * x = 0
行列式转置 值不变
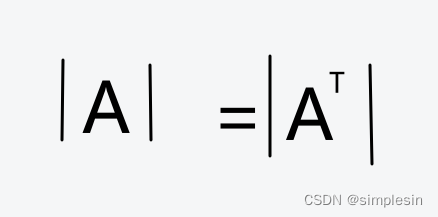
重要关系
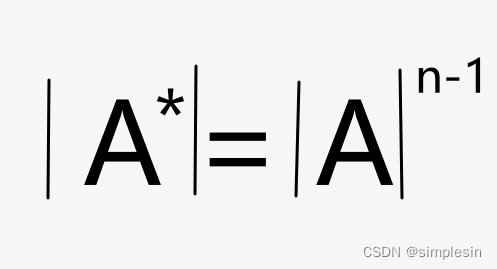
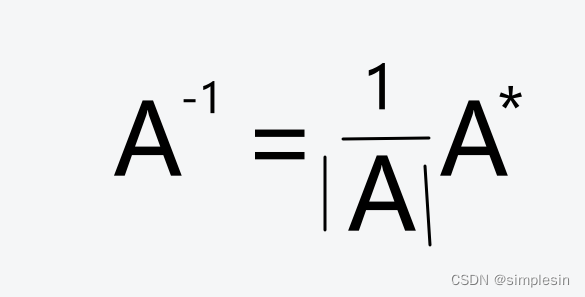
中间相等,取两头

特征值公式
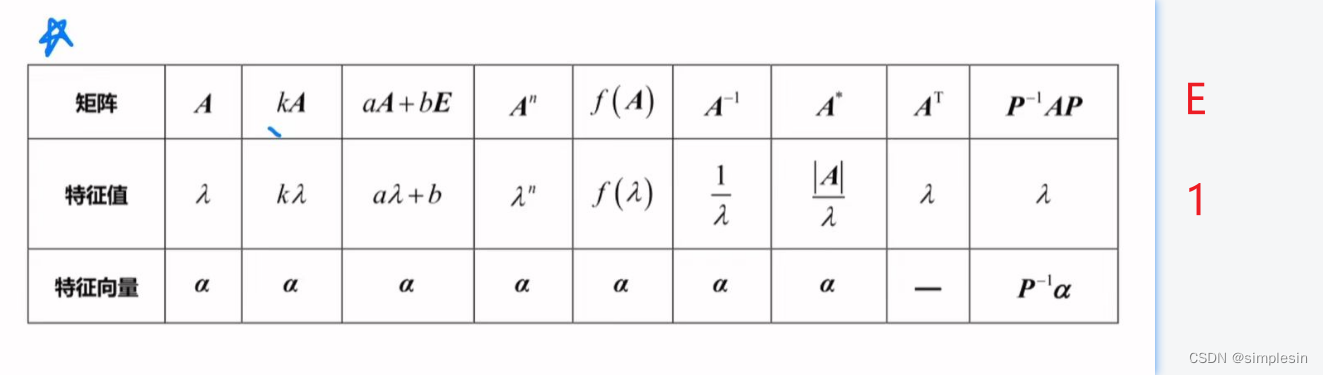
向量正交 = 点积为0
a = (x,y,z) b = (c ,d ,e)
结果为:xc + yd + ze = 0
![]()
拉普拉斯定理
行列式的计算:行列式可以按照任意一行(或列)展开,将其元素与对应的k阶代数余子式相乘后求和,得到的总和即为行列式的值。
代余子式:A
![]()
矩阵的秩
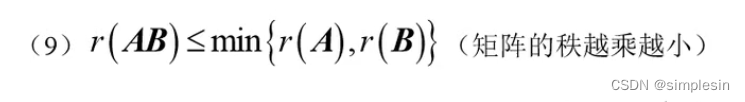
个人理解:
满秩就是没有一整行都是0的情况,同样道理,秩小的话,就说明有比较多零行。
我们又知道,AB,就是对A进行运算,对零是运算不了的,相当于无懈可击。所以,最终决定权在秩小这里。
特征值和特征向量
有多少个自由向量,就要赋几次值
|A|=特征值的乘积 & tr(A)=特征值的和
这都是针对一个n × n 的方阵A
要记要背


增广矩阵