leetcode--二叉树中的最长交错路径
leetcode地址:二叉树中的最长交错路径
给你一棵以 root 为根的二叉树,二叉树中的交错路径定义如下:
选择二叉树中 任意 节点和一个方向(左或者右)。
如果前进方向为右,那么移动到当前节点的的右子节点,否则移动到它的左子节点。
改变前进方向:左变右或者右变左。
重复第二步和第三步,直到你在树中无法继续移动。
交错路径的长度定义为:访问过的节点数目 - 1(单个节点的路径长度为 0 )。
请你返回给定树中最长 交错路径 的长度。
示例 1:
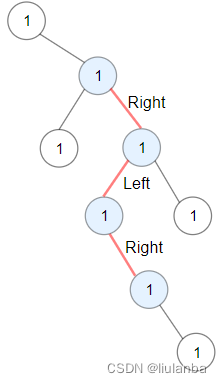
输入:root = [1,null,1,1,1,null,null,1,1,null,1,null,null,null,1,null,1]
输出:3
解释:蓝色节点为树中最长交错路径(右 -> 左 -> 右)。
示例 2:
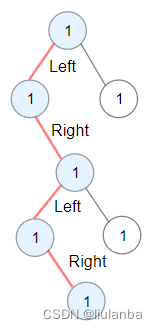
输入:root = [1,1,1,null,1,null,null,1,1,null,1]
输出:4
解释:蓝色节点为树中最长交错路径(左 -> 右 -> 左 -> 右)。
示例 3:
输入:root = [1]
输出:0
提示:
每棵树最多有 50000 个节点。
每个节点的值在 [1, 100] 之间。
实现思路
实现最长交错路径(Longest ZigZag Path)的问题涉及在二叉树中找到一条路径,该路径上的每一步都在左右子树之间交替。具体来说,路径从根节点开始,每次选择左子节点或右子节点,但不能连续两次选择同一个方向。最长交错路径的长度是这条路径上边的数量。
代码详解
- 定义数据结构
首先,定义一个二叉树节点的类,用于表示树中的每个节点。
class TreeNode:def __init__(self, value=0, left=None, right=None):self.value = valueself.left = leftself.right = right
- 初始化类和变量
在解决方案类中,定义一个变量来记录最长交错路径的长度,并初始化该类。
class Solution:def __init__(self):self.max_length = 0
- 定义递归函数
使用深度优先搜索(DFS)来遍历二叉树。在每个节点,记录当前路径的长度,并更新最长交错路径的长度。定义递归函数 dfs 来处理这个过程。
def dfs(node, direction, length):if not node:returnself.max_length = max(self.max_length, length)if direction == 'left':dfs(node.left, 'left', 1) # 重置左边路径长度dfs(node.right, 'right', length + 1) # 继续增加右边路径长度else:dfs(node.left, 'left', length + 1) # 继续增加左边路径长度dfs(node.right, 'right', 1) # 重置右边路径长度
- 调用递归函数
在主函数 longestZigZag 中,从根节点开始,以左和右两个方向调用递归函数 dfs。
def longestZigZag(self, root: TreeNode) -> int:dfs(root, 'left', 0)dfs(root, 'right', 0)return self.max_length
- 将上述步骤组合成完整的代码:
class TreeNode:def __init__(self, value=0, left=None, right=None):self.value = valueself.left = leftself.right = rightclass Solution:def __init__(self):self.max_length = 0def longestZigZag(self, root: TreeNode) -> int:def dfs(node, direction, length):if not node:returnself.max_length = max(self.max_length, length)if direction == 'left':dfs(node.left, 'left', 1) # 重置左边路径长度dfs(node.right, 'right', length + 1) # 继续增加右边路径长度else:dfs(node.left, 'left', length + 1) # 继续增加左边路径长度dfs(node.right, 'right', 1) # 重置右边路径长度dfs(root, 'left', 0)dfs(root, 'right', 0)return self.max_length# 示例二叉树
root = TreeNode(1)
root.left = TreeNode(2)
root.right = TreeNode(3)
root.left.right = TreeNode(4)
root.left.right.left = TreeNode(5)
root.left.right.right = TreeNode(6)# 计算最长交错路径
solution = Solution()
result = solution.longestZigZag(root)
print("最长交错路径长度:", result)
关键点总结
二叉树节点类:用于表示树的结构。
深度优先搜索(DFS):用于遍历二叉树。
递归:在每个节点记录路径的长度,并更新最长交错路径的长度。
方向标志:用 direction 参数来指示当前路径的方向(左或右),并在递归调用时进行交替。
路径长度记录:用 length 参数来记录当前路径的长度,并更新 self.max_length 以记录最长路径的长度。
通过这些步骤,可以有效地计算出二叉树中最长的交错路径。
GO语言实现
package mainimport "fmt"// TreeNode 表示二叉树的节点
type TreeNode struct {Val intLeft *TreeNodeRight *TreeNode
}// Solution 结构体用于记录最长交错路径的长度
type Solution struct {maxLength int
}// NewSolution 初始化 Solution
func NewSolution() *Solution {return &Solution{maxLength: 0}
}// dfs 递归函数遍历二叉树
func (s *Solution) dfs(node *TreeNode, direction string, length int) {if node == nil {return}// 更新最长路径长度if length > s.maxLength {s.maxLength = length}if direction == "left" {s.dfs(node.Left, "left", 1) // 重置左边路径长度s.dfs(node.Right, "right", length+1) // 继续增加右边路径长度} else {s.dfs(node.Left, "left", length+1) // 继续增加左边路径长度s.dfs(node.Right, "right", 1) // 重置右边路径长度}
}// LongestZigZag 计算二叉树的最长交错路径
func (s *Solution) LongestZigZag(root *TreeNode) int {s.dfs(root, "left", 0)s.dfs(root, "right", 0)return s.maxLength
}func main() {// 构建示例二叉树root := &TreeNode{Val: 1}root.Left = &TreeNode{Val: 2}root.Right = &TreeNode{Val: 3}root.Left.Right = &TreeNode{Val: 4}root.Left.Right.Left = &TreeNode{Val: 5}root.Left.Right.Right = &TreeNode{Val: 6}// 计算最长交错路径solution := NewSolution()result := solution.LongestZigZag(root)fmt.Println("最长交错路径长度:", result)
}kotlin实现
class TreeNode(val value: Int) {var left: TreeNode? = nullvar right: TreeNode? = null
}class Solution {private var maxLength = 0private fun dfs(node: TreeNode?, direction: String, length: Int) {if (node == null) return// 更新最长路径长度if (length > maxLength) {maxLength = length}if (direction == "left") {dfs(node.left, "left", 1) // 重置左边路径长度dfs(node.right, "right", length + 1) // 继续增加右边路径长度} else {dfs(node.left, "left", length + 1) // 继续增加左边路径长度dfs(node.right, "right", 1) // 重置右边路径长度}}fun longestZigZag(root: TreeNode?): Int {dfs(root, "left", 0)dfs(root, "right", 0)return maxLength}
}fun main() {// 构建示例二叉树val root = TreeNode(1)root.left = TreeNode(2)root.right = TreeNode(3)root.left?.right = TreeNode(4)root.left?.right?.left = TreeNode(5)root.left?.right?.right = TreeNode(6)// 计算最长交错路径val solution = Solution()val result = solution.longestZigZag(root)println("最长交错路径长度: $result")
}