当前位置：首页 > news >正文

Matlab绘制隐函数总结-二维和三维

news 2025/6/23 0:22:28

1.二维隐函数

二维隐函数满足 $f (x, y) = 0$ ，这里无法得到 $y = f (x)$ 的形式。不能通过普通函数绘制。

我们要关注的是使用fplot函数和fimplicit函数。
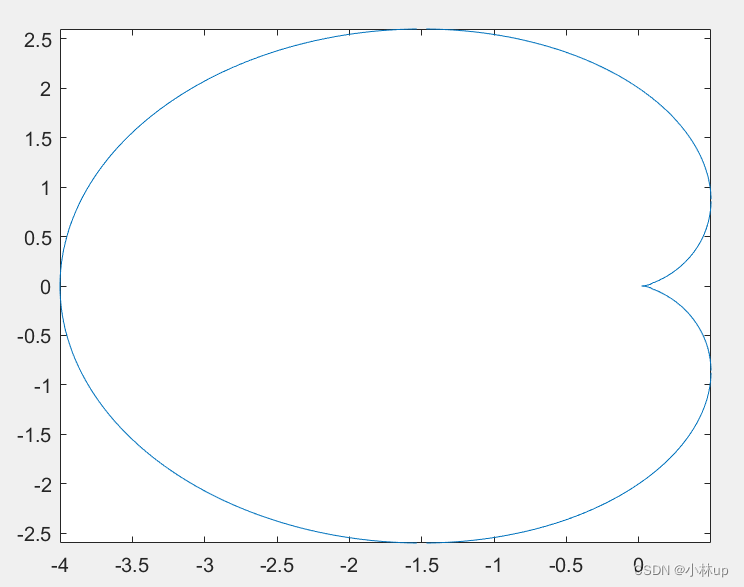
在这里插入图片描述

第1种情况：基本隐函数

基本的隐函数形式形如：

$x2+y2+2x=2(x2+y2)12x^{2}+y^{2}+2 x=2\left(x^{2}\right.\left.+y^{2}\right)^{\frac{1}{2}}$

原来有个ezplot函数的，但是现在Matlab不推荐使用了，可能要慢慢淘汰掉了。老版的写法是
ezplot('x^2+y^2+2*x=2*sqrt(x^2+y^2)') 
或者
syms x y 
ezplot(x^2+y^2+2*x-2*sqrt(x^2+y^2)) 
（后面我们也不再谈ezplot函数）

下面是官方推荐的写法：

使用fplot函数

fplot('x^2+y^2+2*x=2*sqrt(x^2+y^2)')

使用fimplicit函数

注意和fplot函数不同，Matlab官方提示：为了获得最佳性能和避免产生警告消息，请使用按元素运算符。例如，使用 x.*y 而不是 x*y。

fimplicit( x.^2+y.^2+2.*x-2.*sqrt(x.^2+y.^2))

或者

fimplicit(@(x,y) x.^2+y.^2+2.*x-2.*sqrt(x.^2+y.^2))

总结：一般的隐函数可以使用fplot函数或者fimplicit函数绘制。

第2种情况：隐函数带变量

形如：

$x2+y2+ax=a(x2+y2)12x^{2}+y^{2}+a x=a\left(x^{2}+y^{2}\right)^{\frac{1}{2}}$

根据实际需要可将 $a$ 事先具体赋值, 但使用中应注意,绘图语句不能简单采用前面基本格式的形式 ,不能写作，会报错

a = 2; 
fplot('x^2+y^2+a*x-a*sqrt(x^2+y^2)');

因为函数包括单引号时,相当于是符号表达式,变量a的值作为一个参数,不能传进函数,导致fplot()不能正常绘图。

使用fimplicit函数

fplot函数测试了不行，使用fimplicit函数下面的代码是可以的。

a=2;
syms x y
fimplicit(x.^2+y.^2+ a.*x-a.*sqrt(x.^2+y.^2))

总结：带有未知参数的隐函数使用fimplicit函数绘制

第3种情况：带有多个变量的隐函数组的绘图

形如：

$y)=x+y^2=a,\quad g(x, y)=x^2-y=b$

不妨令：

$a = 3, b = - 3$

使用fimplicit函数

因为还是带有未知参数的隐函数，我们还是用使用fimplicit函数绘制。

a=3;b=-3;
syms x y
f=x+y^2-a;
g=x^2-y-b;
fimplicit(f);
hold on;
fimplicit(g)
title('x+y^2-a=0 x^2-y-b=0 a=3 b=-3')

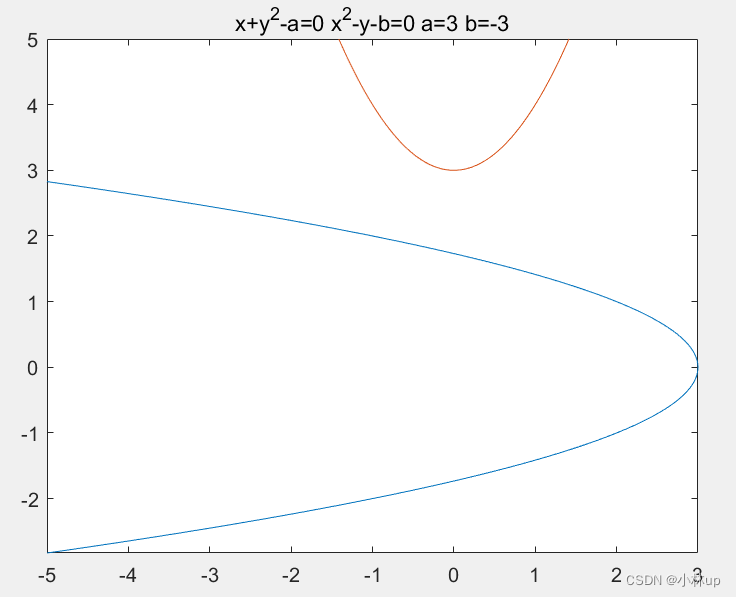
在这里插入图片描述

总结：带有多个变量的隐函数组使用fimplicit函数绘制，加上hold on命令

2.三维隐函数

三维隐函数满足 $f (x, y, z) = 0$ ，这里无法得到 $z = f (x, y)$ 的形式。不能通过普通函数绘制。

我们要关注的是使用等面值计算函数isosurface和面元渲染函数patch分布实现三维隐函数曲面的绘制方法。

我们使用isosurface的调用方式是

[f,v] = isosurface(X,Y,Z,V,isovalue)

官方的解释是该语句返回由isovalue指定的某个等值面的表面(Faces)和顶点(Vertices)数据,并存放在单独的数组f、v中。我们绘制的是 $v = f (x, y, z) = 0$ 的三维图形，则isovalue=0。

patch函数是面元渲染函数，对曲面进行修饰，相关的调用方式是：patch(X,Y,Z,C)

patch(X,Y,Z,C)

它以三维坐标(X,Y,Z)为顶点,构造三维曲面,c是R G B颜色向量。另一个相关的调用方式是：

patch('Faces',F,'Vertices',V)

它通过包含Faces、Vertices两个的数组F、V来构造三维曲面,F和V可以由等值面函数isosurface计算而得。

对于三元显函数 $v = f (x, y, z)$ 来说,当 $v = 0$ 时的等值面就是 $z = g (x, y)$ 的三维曲面。isosurface函数可以计算 $v = 0$ 的等值面,返回结果包括表面和顶点数据,并存放于数组 $f$ 、 $v$ 中,再输入给patch函数,能构造三维曲面,还可以根据需要设置颜色、亮度、三维视角等。画图的步骤可以归纳为：

(1)用meshgrid函数产生网格点,同时可确定坐标范围。
(2)引用隐函数表达式计算格点函数值val。
(3)调用[f,v]=isosurface(x,y,z,val,0)计算隐函数等值面并返回到f、v。
(4)调用patch(‘Faces’,f,‘Vertices’,v,‘facecolor’,‘interp’,‘EdgeColor’,‘k’)对曲面修饰。

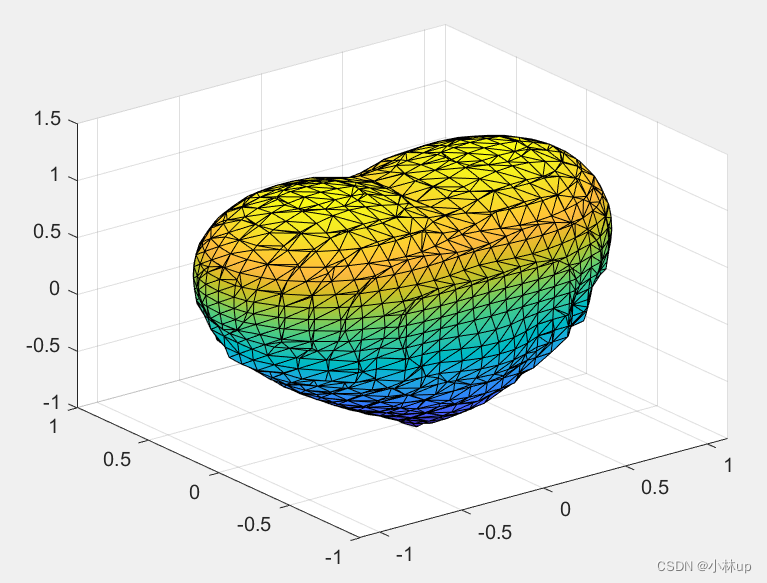
[x,y,z]=meshgrid(-1.5:0.1:1.5,-1.5:0.1:1.5,-1.5:0.1:1.5);
v=(x.^2+(9/4)*y.^2+z.^2-1).^3-x.^2.*z.^3-(9/80)*y.^2.*z.^3;
[f,v]=isosurface(x,y,z,v,0);
p=patch('Faces',f,'Vertices',v,'CData',v(:,3),'facecolor','interp',...'EdgeColor','k');
view(3); grid on;