双指针系列第 8 篇:盛水最多的容器。几句话讲明白!

Leetcode 题目链接
思路
取首尾双指针和水量如下所示,设高度函数为 h ( i ) h(i) h(i),在下图中 h ( l ) < h ( r ) h(l) < h(r) h(l)<h(r)。
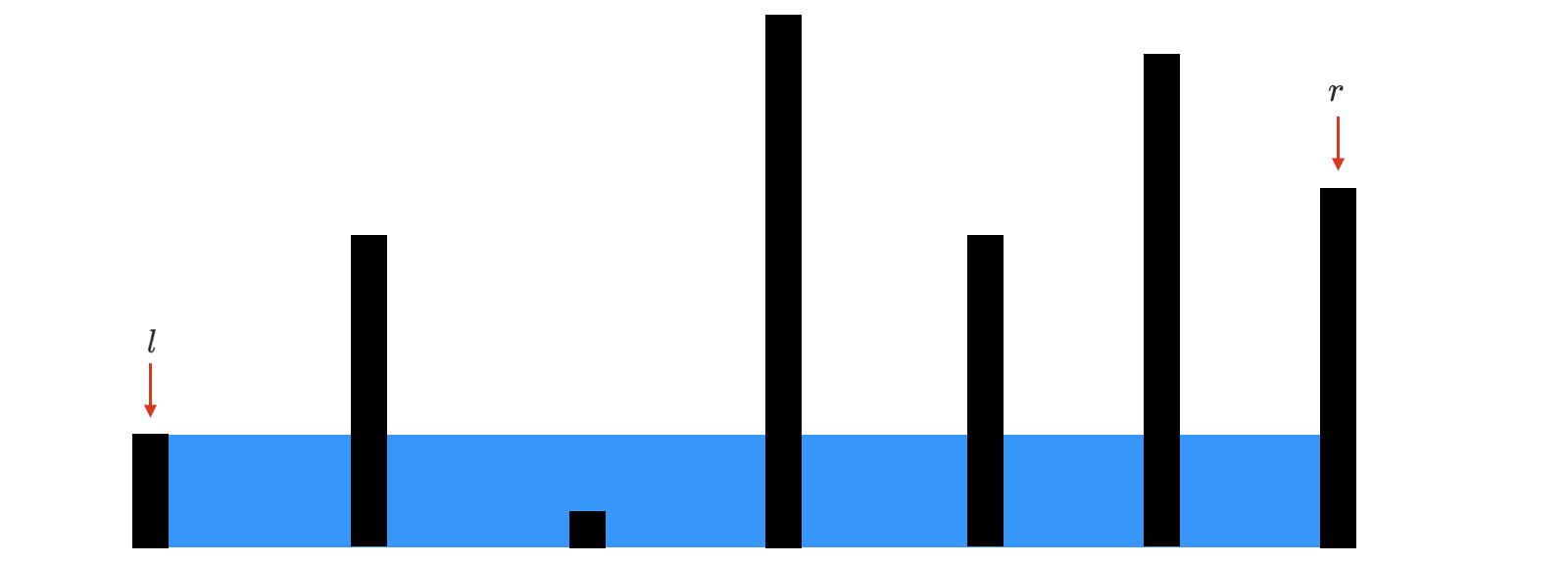
观察以 l l l 为左边界所能构成的其他水量,与矮的右边界搭配结果如下。
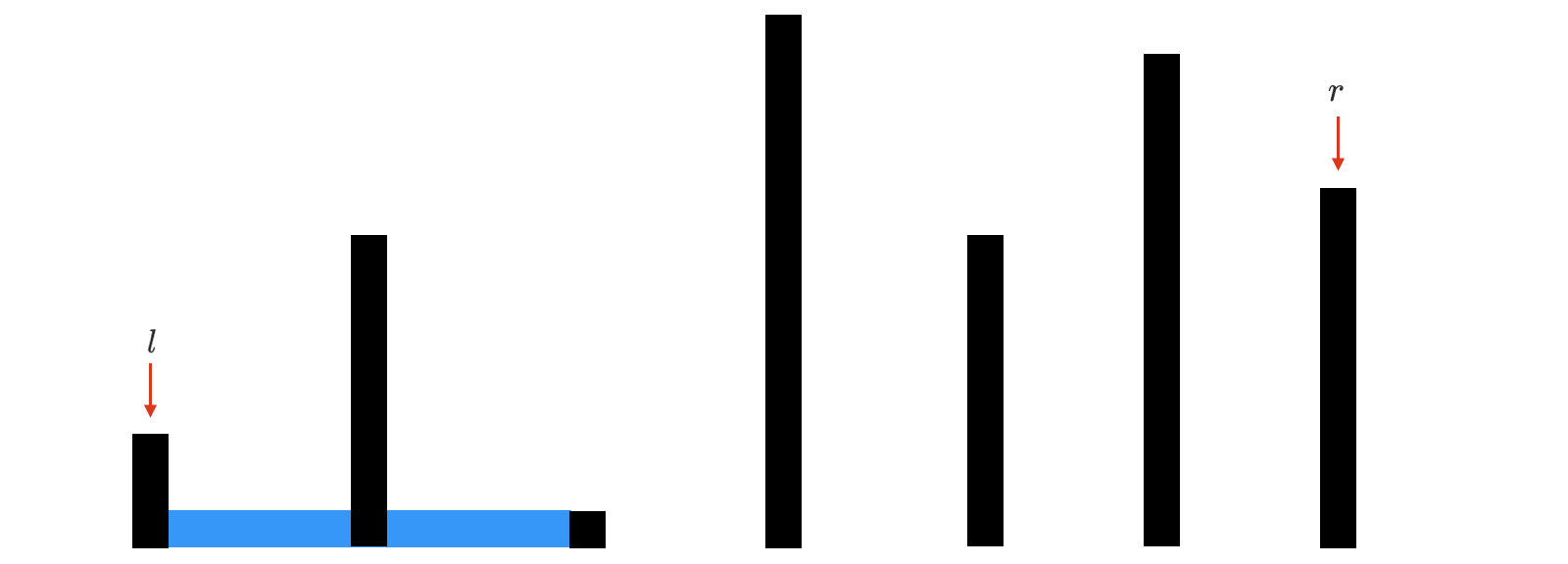
与高的右边界搭配结果如下。
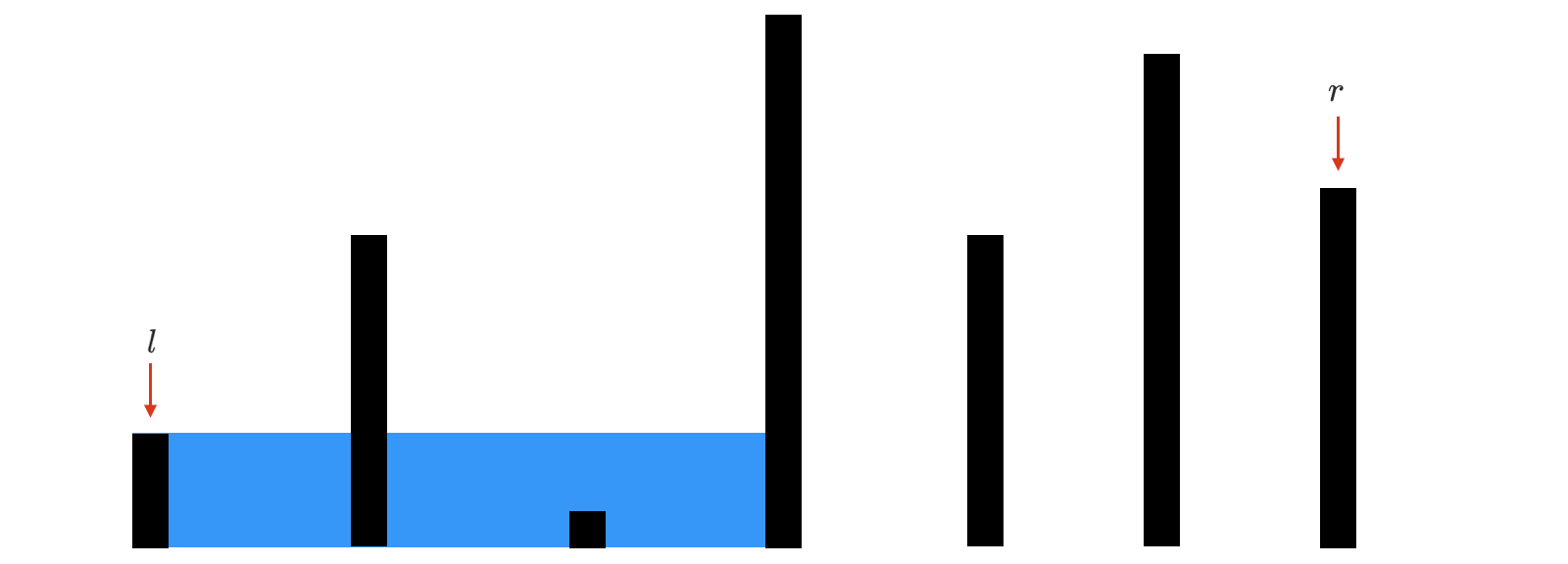
我们可以发现水量都会变小,即无法通过当前 l l l 获得更大的水量,可在记录水量后舍弃 l l l,使其右移。
如果初始 h ( l ) > h ( r ) h(l) > h(r) h(l)>h(r), 则镜像处理,令 r r r左移。
如果初始 h ( l ) = h ( r ) h(l) = h(r) h(l)=h(r),任意移动均可。
此后循环分析这个过程并移动指针即可。
严谨证明
假设初始 h ( l ) < h ( r ) h(l) < h(r) h(l)<h(r),当前可容纳的水量记为 c = ( r − l ) × h ( l ) c = (r - l) \times h(l) c=(r−l)×h(l)。
∀ i ∈ ( l , r ) \forall i \in (l, r) ∀i∈(l,r), i i i 和 l l l 作为边界对应的可容纳水量记为 c ′ = ( i − l ) × m i n { h ( i ) , h ( l ) } c' = (i - l) \times min\{h(i),\ h(l)\} c′=(i−l)×min{h(i), h(l)},其中:
- i − l < r − l i - l < r - l i−l<r−l
- m i n { h ( i ) , h ( l ) } ≤ h ( l ) min\{h(i),\ h(l)\} \leq h(l) min{h(i), h(l)}≤h(l)
故 c ′ < c c' < c c′<c,可在记录水量后舍弃 l l l,令 l l l 右移,因为无法通过 l l l 获得更大的水量。
余下分析同上。
代码
仅提供 java 代码。
class Solution {public int maxArea(int[] height) {int l = 0;int r = height.length - 1;int maxCap = 0; // 待返回的最大水量while (l < r) {int cap = (r - l) * Math.min(height[l], height[r]);maxCap = Math.max(maxCap, cap);if (height[l] < height[r]) {l++;} else {r--;}}return maxCap;}
}
复杂度
时间: Θ ( n ) \Theta(n) Θ(n)
空间: Θ ( 1 ) \Theta(1) Θ(1)
推广
以下皆为个人所著,兼顾了职场面试和本硕阶段的学术考试。
- 附个人题解的双指针题单
- 图论入门
- 图论进阶
点赞关注不迷路,祝各位早日上岸,飞黄腾达!
