当前位置：首页 > news >正文

【算法学习】射线法判断点在多边形内外（C#）以及确定内外两点连线与边界的交点

news 2025/7/15 10:23:04

1.前言：

在GIS开发中，经常会遇到确定一个坐标点是否在一块区域的内部这一问题。
如果这个问题不是一个单纯的数学问题，例如：在判断DEM、二维图像像素点、3D点云点等含有自身特征信息的这些点是否在一个区域范围内部的时候，可以结合其高程信息、RGB信息、深度信息来辅助处理，相比与单纯从数学角度来看更简单、快速。

举几个我认为正确的例子：SLAM中前端角点的选取，利用的是OpenCV来提取；DEM提取边界，根据周围高程的有无；PS中扣出某物边界，利用的是RGB差异性；点云提取可以利用深度信息（本质也是RGB）来做。

但是，如果我现在只拥有点的坐标，该问题就变成一个数学问题了。

2.射线法：

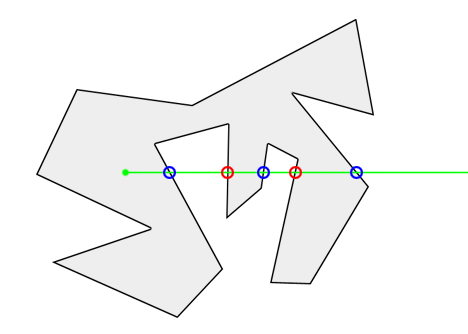
在这里插入图片描述

该算法基本思路是从待定点朝任意方向射出一条射线（通常是水平向右），判断该射线与多边形边的交点个数。一般来说，交点个数为偶数（包括0），点在外部；交点个数为奇数，点在内部。
因为点和图形的位置是固定不动的，所以射线的朝向，对于最终的交点个数，也就是位置结果是没有影响的。

2.1 算法介绍

在分析前要先明白几个问题：

如果没有特殊需求，待求点在图形的边界（线段、交点）上，默认是属于图形内部的。
默认待求点的射线沿着x轴方向水平射出（水平向右）。
射线经过边界交点情况很常见，为了防止上一个线段的末顶点和下一个线段的首顶点（这两个是一个点）被算作两次，所以只看线段的y更小的一端，即参数方程的值域符号：[y1,y2)。
假如逆时针遍历各边，看下图示例：

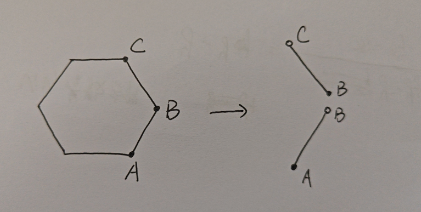
（1）从简单情况开始分析：
最简单的情况当属一个规整的四边形，射线与四边形的交点个数存在的情况有：0，1，2。
如果，不考虑穿过顶点，不考虑点的射线与边平行（重合），就单纯考虑穿的全部是边，遇到这种情况：
先建立遍历边的参数方程，找到射线与参数方程的交点，再判断交点X交和待定点的位置关系。
在这里插入图片描述
如果P在X交左侧，有一个交点则计数+1；
如果P和X交是一个点，则说明P在边界线段上，直接返回true；
如果在X交右侧，没有交点。

注意：这里的上下yi和yj的取值，要包含下界，不包含上界，否则会被计算两次，而且这样可以有效忽略水平边界而待求点在左侧的问题。
当然，反过来也可以，都选择更大的y值。

（2）我认为的几种特殊情况，这几种特殊情况有特点：就是无法找到线段去做参数方程或者实际交点无数个。这几种特殊情况需要单独处理。

待求点就是边界交点：通过坐标判断，直接返回是否在边界内。
待求点在水平边界线上：通过坐标判断，直接返回是否在边界内。
待求点在水平边界线左侧：配合前后该水平边界先后线段参数方程的值域，这种情况可以直接忽略！（忽略不是没有考虑）

2.2 C#代码实现

using System;
using System.Collections.Generic;public class Point
{public double X { get; set; }public double Y { get; set; }public Point(double x, double y){X = x;Y = y;}
}
public class Polygon
{private List<Point> vertices;public Polygon(List<Point> points){vertices = points;}public bool IsPointInside(Point testPoint){int intersectionCount = 0;int vertexCount = vertices.Count;for (int i = 0, j = vertexCount - 1; i < vertexCount; j = i++){Point vi = vertices[i];Point vj = vertices[j];// 检查测试点是否在顶点上if ((vi.X == testPoint.X && vi.Y == testPoint.Y) ||(vj.X == testPoint.X && vj.Y == testPoint.Y)){return true;}// 检查测试点是否在水平边上if (vi.Y == vj.Y && vi.Y == testPoint.Y){if (testPoint.X > Math.Min(vi.X, vj.X) && testPoint.X < Math.Max(vi.X, vj.X)){return true;}}// 检查testpoint.y是否在两个端点的中间//if ((vi.Y > testPoint.Y) != (vj.Y > testPoint.Y)) // 这行代码更简单，但是有点小小的不直观if ((vi.Y <= testPoint.Y && vj.Y > testPoint.Y) || (vj.Y <= testPoint.Y && vi.Y > testPoint.Y)){double intersectionX = (vj.X - vi.X) * (testPoint.Y - vi.Y) / (vj.Y - vi.Y) + vi.X;// 处理边界情况if (testPoint.X == intersectionX){return true;}if (testPoint.X < intersectionX){intersectionCount++;}}}// 如果交点数为奇数，则点在多边形内部return intersectionCount % 2 != 0;}
}
internal class Program
{static void Main(string[] args){List<Point> vertices = new List<Point>{new Point(0,0),new Point(1,0),new Point(2,-1),new Point(3,0),new Point(5,0),new Point(5,1),new Point(4,1),new Point(4,2),new Point(3,3),new Point(3,4),new Point(2,4),new Point(2,3),new Point(1,3),new Point(1,4),new Point(0,4),new Point(0,2),new Point(-1,1),};Polygon polygon = new Polygon(vertices);List<Point> testPoint = new List<Point>();for (int i = -1; i < 6; i++){for (int j = -1; j < 7; j++){testPoint.Add(new Point(i, j));}}foreach (var p in testPoint){Console.WriteLine($"p点坐标：（{p.X}, {p.Y}）,是否在图形内部：{polygon.IsPointInside(p)}");}Console.ReadKey();}
}

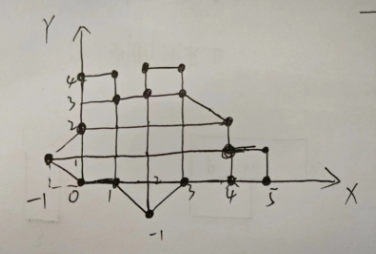
在这里插入图片描述
用for循环写了一个从（-1，-1）到（5，6）覆盖的测试点，最后结果：

p点坐标：（-1, -1）,是否在图形内部：False|p点坐标：（-1, 0）,是否在图形内部：False
p点坐标：（-1, 1）,是否在图形内部：True|p点坐标：（-1, 2）,是否在图形内部：False
p点坐标：（-1, 3）,是否在图形内部：False|p点坐标：（-1, 4）,是否在图形内部：False
p点坐标：（-1, 5）,是否在图形内部：False|p点坐标：（-1, 6）,是否在图形内部：False
p点坐标：（0, -1）,是否在图形内部：False|p点坐标：（0, 0）,是否在图形内部：True
p点坐标：（0, 1）,是否在图形内部：True|p点坐标：（0, 2）,是否在图形内部：True
p点坐标：（0, 3）,是否在图形内部：True|p点坐标：（0, 4）,是否在图形内部：True
p点坐标：（0, 5）,是否在图形内部：False|p点坐标：（0, 6）,是否在图形内部：False
p点坐标：（1, -1）,是否在图形内部：False|p点坐标：（1, 0）,是否在图形内部：True
p点坐标：（1, 1）,是否在图形内部：True|p点坐标：（1, 2）,是否在图形内部：True
p点坐标：（1, 3）,是否在图形内部：True|p点坐标：（1, 4）,是否在图形内部：True
p点坐标：（1, 5）,是否在图形内部：False|p点坐标：（1, 6）,是否在图形内部：False
p点坐标：（2, -1）,是否在图形内部：True|p点坐标：（2, 0）,是否在图形内部：True
p点坐标：（2, 1）,是否在图形内部：True|p点坐标：（2, 2）,是否在图形内部：True
p点坐标：（2, 3）,是否在图形内部：True|p点坐标：（2, 4）,是否在图形内部：True
p点坐标：（2, 5）,是否在图形内部：False|p点坐标：（2, 6）,是否在图形内部：False
p点坐标：（3, -1）,是否在图形内部：False|p点坐标：（3, 0）,是否在图形内部：True
p点坐标：（3, 1）,是否在图形内部：True|p点坐标：（3, 2）,是否在图形内部：True
p点坐标：（3, 3）,是否在图形内部：True|p点坐标：（3, 4）,是否在图形内部：True
p点坐标：（3, 5）,是否在图形内部：False|p点坐标：（3, 6）,是否在图形内部：False
p点坐标：（4, -1）,是否在图形内部：False|p点坐标：（4, 0）,是否在图形内部：True
p点坐标：（4, 1）,是否在图形内部：True|p点坐标：（4, 2）,是否在图形内部：True
p点坐标：（4, 3）,是否在图形内部：False|p点坐标：（4, 4）,是否在图形内部：False
p点坐标：（4, 5）,是否在图形内部：False|p点坐标：（4, 6）,是否在图形内部：False
p点坐标：（5, -1）,是否在图形内部：False|p点坐标：（5, 0）,是否在图形内部：True
p点坐标：（5, 1）,是否在图形内部：True|p点坐标：（5, 2）,是否在图形内部：False
p点坐标：（5, 3）,是否在图形内部：False|p点坐标：（5, 4）,是否在图形内部：False
p点坐标：（5, 5）,是否在图形内部：False|p点坐标：（5, 6）,是否在图形内部：False