力扣300. 最长递增子序列(动态规划)
Problem: 300. 最长递增子序列
文章目录
- 题目描述
- 思路及解法
- 复杂度
- Code
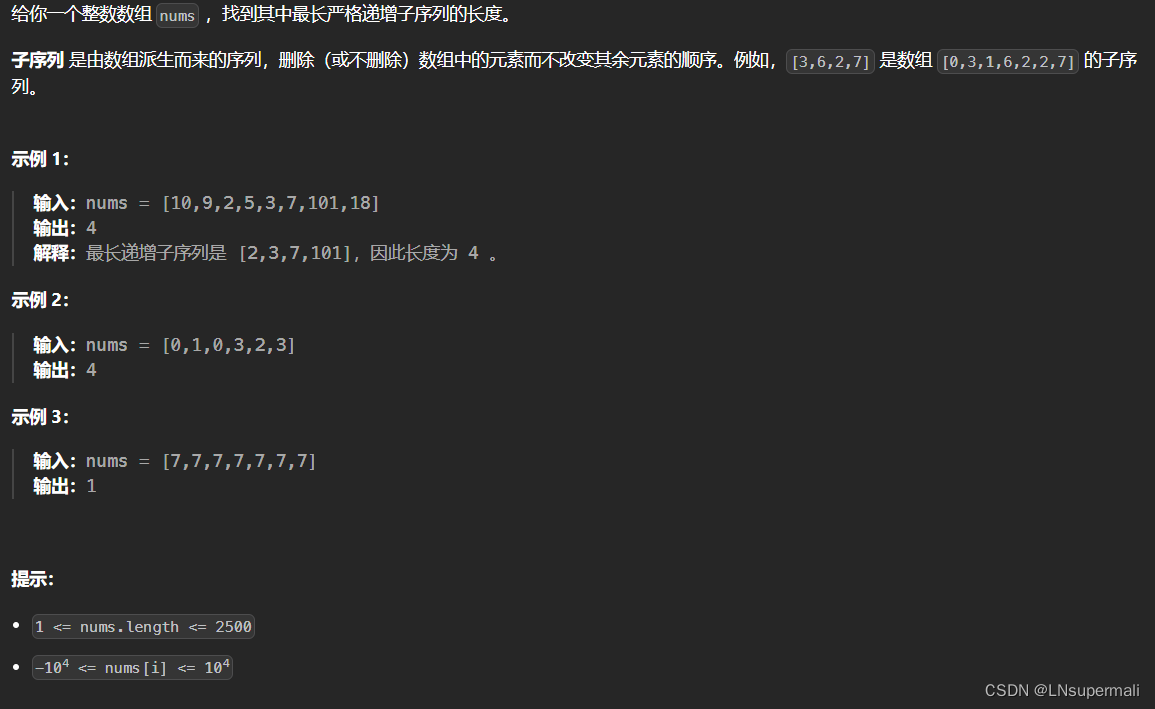
题目描述
思路及解法
明确题目涉及到求取最值问题因此我们可以考虑使用动态规划来解决问题
1.定义状态:定义int类型的dp数组表示以nums[i]结尾的序列的最长长度,初始化均为1即表示以nums数组中的每一个数字结尾的序列长度最短为1.
2.状态转移:假设现在已经得出dp[i-1]的长度,再进一步求取dp[i]:此时我么和从数组nums[0 ~ j] 其中(j < i)寻找,若nums[i] < nums[i]则dp[i] = max(dp[i], dp[j] + 1),因为根据上述dp数组的状态定义dp[j]是表示以nums[j]结尾的最长递增子序列,此时nums[j] < nums[i]则dp[i]要在dp[i]和dp[j] + 1中选取一个最大值
复杂度
时间复杂度:
O ( n 2 ) O(n^2) O(n2);其中 n n n表示数组nums的大小
空间复杂度:
O ( n ) O(n) O(n)
Code
class Solution {/*** Longest Increasing Subsequence** @param nums Given array* @return int*/public int lengthOfLIS(int[] nums) {int[] dp = new int[nums.length];for (int i = 0; i < nums.length; ++i) {dp[i] = 1;}for (int i = 0; i < nums.length; ++i) {for (int j = 0; j < i; ++j) {if (nums[j] < nums[i]) {dp[i] = Math.max(dp[i], dp[j] + 1);}}}int res = 0;for (int i = 0; i < nums.length; ++i) {res = Math.max(res, dp[i]);}return res;}
}