C语言的数据结构:树与二叉树(哈夫曼树篇)
前言
上篇讲完了二叉树,二叉树的查找性能要比树好很多,如平衡二叉树保证左右两边节点层级相差不会大于1,其查找的时间复杂度仅为 l o g 2 n log_2n log2n,在两边层级相同时,其查找速度接近于二分查找。1w条数据,平衡二叉树的查找最差情况下仅有14次,而普通树(也就是多叉树),如果每层都有100个节点,第二层可以接近1w(9999)条数据,其查找的时间复杂度也高的多。
但多叉树在文件系统和数据库的应用中表现很好,像自平衡多叉树(B - 树)其在磁盘io操作的速度也更好,像 mysql 的索引采取就是 B+ 树。
如果上面的二叉树和多叉树在表现中已经这么好了,为什么还要有哈夫曼树这种结构?
哈夫曼树的应用场景主要是数据压缩,特别是通过哈夫曼编码进行文件压缩。哈夫曼树的设计目的是通过构建一棵带权路径长度最小的二叉树,来减少编码长度,提高压缩效率。前提是哈夫曼树的构建要基于权重,也就是这么多的数据,它要知道哪些是经常被访问的,经常访问的则权重高,反之则权重低。
像下面这棵树,如果我们已经知道 D的访问次数较高,一共要访问5次,而B的访问次数只有1次,则将D、B全部访问完需要:
B:路径A -> B, 路径为1,访问次数为1,总访问 路长为 1 \color{orange}路长为1 路长为1。
D:路径A -> B -> D ,路径为2,访问次数为5,总访问 路长为 10 \color{orange}路长为10 路长为10。
D、B全部访问:1 + 10 = 11 。

但如果按照哈夫曼树的构造,会生成下面这样。
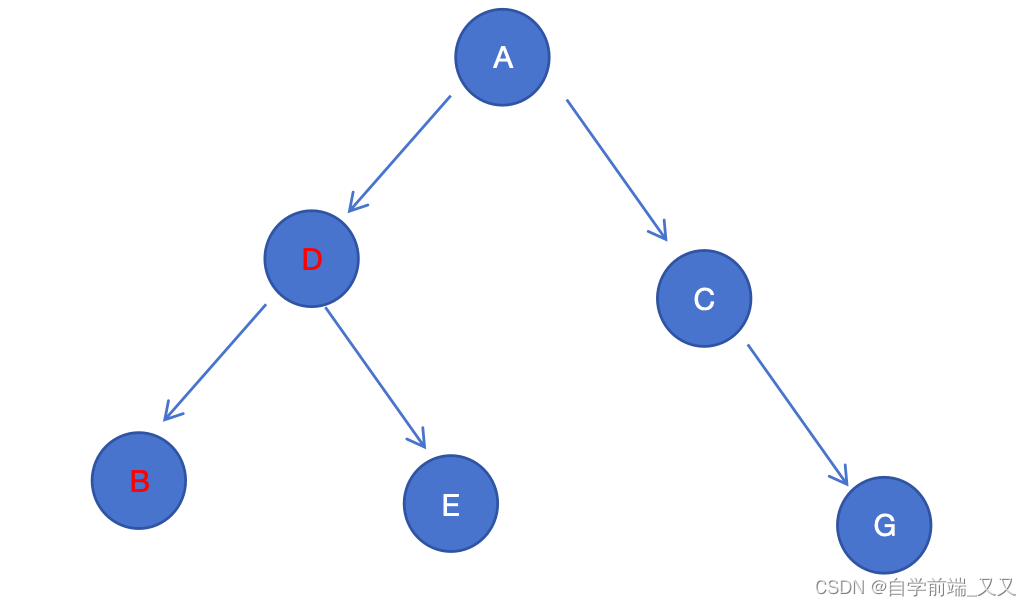
我们已经知道 D的访问次数较高,一共要访问5次,而B的访问次数只有1次,则将D、B全部访问完需要:
B:路径A -> D -> B, 路径为2,访问次数为1,总访问 路长为 2 \color{orange}路长为2 路长为2。
D:路径A -> D ,路径为1,访问次数为5,总访问 路长为 5 \color{orange}路长为5 路长为5。
D、B全部访问:5 + 2 = 7 。
可以看到,存储同样的数据,仅仅只是按照权重换了数据的位置,就可以减少总访问路径长度。
那一个数据当中,又是如果知道哪些数据会经常访问,哪些是不经常呢?一个是来源于对过往的总结。如一个学校的成绩分布有[小于50、50-80、80-100],而经常几次考试的结果发现,大多数都在50-80的区域,那这个哈夫曼树的最
接近根节点的应该是 50-80 。也有些是通过对文字的出现次数总结,如有人统计出26个英文字母中,什么字母使用的最多,什么字母使用的最少,则也可以构建出基于此的哈夫曼树。而哈夫曼编码就来源于此。
