当前位置：首页 > news >正文

LeetCode 算法：二叉树的层序遍历 c++

news 2025/8/5 3:24:25

原题链接🔗：二叉树的层序遍历
难度：中等⭐️⭐️

题目

给你二叉树的根节点 root ，返回其节点值的层序遍历。（即逐层地，从左到右访问所有节点）。

示例 1：
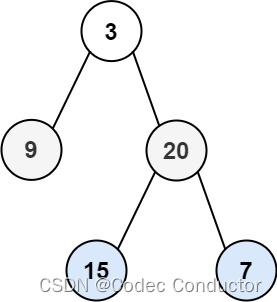
在这里插入图片描述
输入：root = [3,9,20,null,null,15,7]
输出：[[3],[9,20],[15,7]]

示例 2：
输入：root = [1]
输出：[[1]]

示例 3：
输入：root = []
输出：[]

提示：

树中节点数目在范围 [0, 2000] 内
-1000 <= Node.val <= 1000

二叉树

二叉树是一种特殊的树形数据结构，其中每个节点最多有两个子节点，通常称为左子节点和右子节点。二叉树的特点是：

每个节点都包含一个数据元素和两个指向其他节点的指针（或链接），分别指向左子节点和右子节点。
左子节点的值总是小于或等于其父节点的值。
右子节点的值总是大于或等于其父节点的值。

二叉树的一些常见类型包括：

完全二叉树：除了最后一层外，每一层都被完全填满，并且最后一层的节点尽可能地集中在左侧。
满二叉树：所有层都被完全填满。
平衡二叉树：任何两个子树的高度差不超过1，这种树可以保证操作的平衡性，常用于数据库索引。
二叉搜索树（BST）：左子树的所有节点的值小于当前节点的值，右子树的所有节点的值大于当前节点的值。

二叉树的常见操作包括：

插入：在树中插入一个新的节点，同时保持二叉树的性质。
删除：从树中删除一个节点，同时保持二叉树的性质。
搜索：在树中查找一个特定的值。
遍历：按照特定的顺序访问树中的所有节点，常见的遍历方式有：
- 前序遍历：先访问根节点，然后左子树，最后右子树。
- 中序遍历：先访问左子树，然后根节点，最后右子树。
- 后序遍历：先访问左子树，然后右子树，最后根节点。
- 层序遍历：按照层次顺序访问节点，通常使用队列实现。

二叉树在计算机科学中有着广泛的应用，例如在文件系统、数据库索引、搜索算法、表达式解析等领域。

下面是一个简单的C++实现二叉树节点的示例：

struct TreeNode {int val;TreeNode *left;TreeNode *right;TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
};

这个结构定义了一个二叉树节点，其中val是节点存储的数据，left和right是指向左右子节点的指针。

二叉树层序遍历

二叉树的层序遍历是一种按层次顺序访问所有节点的遍历方式，通常使用队列来实现。下面是二叉树层序遍历的步骤：

初始化：创建一个队列来存储节点，将根节点加入队列。
循环遍历：当队列非空时，执行以下操作：
- 取出队列中的第一个节点，访问该节点的值。
- 将该节点的左子节点和右子节点（如果它们存在）加入队列。
收集结果：将每一层访问的节点值存储在一个列表中，然后将这些列表存储在一个更大的列表中，形成层序遍历的结果。

题解

队列法

解题思路：

二叉树的层序遍历是一种常见的树遍历算法，其目的是按照从上到下，从左到右的顺序访问二叉树中的所有节点。层序遍历通常使用队列来实现，以下是一个解题思路：

初始化：创建一个队列queue来存储二叉树的节点，首先将根节点root入队。

遍历条件：当队列不为空时，执行以下步骤。

获取队列大小：记录当前层的节点数level_size，这可以通过队列的大小来获取。

逐层遍历：使用一个循环，循环次数为level_size，每次循环从队列中出队一个节点，并访问该节点的值。

处理子节点：对于每个出队的节点，如果它有左子节点，将左子节点入队；如果它有右子节点，也将右子节点入队。

收集结果：将每层访问的节点值存储在一个列表中，所有层的列表可以存储在一个更大的列表中，形成层序遍历的结果。

返回结果：遍历结束后，返回包含所有层节点值的列表

复杂度：

时间复杂度：每个点进队出队各一次，故渐进时间复杂度为 O(n)。
空间复杂度：队列中元素的个数不超过 n 个，故渐进空间复杂度为 O(n)。

c++ demo：

#include <iostream>
#include <vector>
#include <queue>// 定义二叉树节点结构
struct TreeNode {int val;TreeNode* left;TreeNode* right;TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
};// 层序遍历函数
std::vector<std::vector<int>> levelOrder(TreeNode* root) {std::vector<std::vector<int>> result;if (!root) return result;  // 如果根为空，直接返回空结果std::queue<TreeNode*> q;  // 使用队列来存储节点q.push(root);  // 将根节点入队while (!q.empty()) {int level_size = q.size();  // 当前层的节点数量std::vector<int> current_level;  // 当前层的节点值列表for (int i = 0; i < level_size; ++i) {TreeNode* node = q.front();  // 取出队列前端的节点q.pop();  // 弹出队列current_level.push_back(node->val);  // 将节点值加入到当前层列表// 将非空的左右子节点入队if (node->left) q.push(node->left);if (node->right) q.push(node->right);}result.push_back(current_level);  // 将当前层的节点值列表加入到结果中}return result;
}// 辅助函数：释放二叉树内存
void deleteTree(TreeNode* node) {if (!node) return;deleteTree(node->left);deleteTree(node->right);delete node;
}int main() {// 创建一个示例二叉树//       3//      / \//     9  20//       /  \//      15   7TreeNode* root = new TreeNode(3);root->left = new TreeNode(9);root->right = new TreeNode(20);root->right->left = new TreeNode(15);root->right->right = new TreeNode(7);// 层序遍历二叉树std::vector<std::vector<int>> levels = levelOrder(root);// 打印层序遍历结果for (const auto& level : levels) {for (int val : level) {std::cout << val << " ";}std::cout << std::endl;}// 释放二叉树内存deleteTree(root);return 0;
}