《机器学习》基础概念之【P问题】与【NP问题】
《机器学习》基础概念之【P问题】与【NP问题】
这里写目录标题
- 《机器学习》基础概念之【P问题】与【NP问题】
- 一、多项式&时间复杂度
- 1.1. 多项式
- 1.2.时间复杂度
- 二、P问题 & NP问题
- 2.1. P问题
- 2.2.NP问题
- 2.3.举例理解NP问题-TSP旅行商推销问题
- 三、NP-hard问题&NP-C问题
- 3.1.NP-hard问题
- 3.2. NP-C问题
- 四、P&NP的联系
- 4.1. 理想:NP问题 = P问题
- 4.2.现实:我们仍然相信 P问题!=NP问题
一、多项式&时间复杂度
1.1. 多项式
axn+bxn−1+cax^{n} + b x^{n-1}+caxn+bxn−1+c 形如这种形式的就被称为 xxx 的最高位为 nnn 的多项式。
1.2.时间复杂度
定义为:随着问题规模的增大,算法执行时间增长的快慢。
它可以用来表示一个算法运行的 时间效率\red{时间效率}时间效率。
举个例子,冒泡排序的时间复杂度为 O(n2)O(n^2)O(n2) , 取其最高次,可以看出,这是一个时间复杂度为多项式的表示方式。
二、P问题 & NP问题
2.1. P问题
P(deterministic polynomial time question):
多项式时间问题,简称 P 问题,意思是能在多项式时间内解决的问题。
简单理解是算起来很快的问题。
2.2.NP问题
NP(No-deterministic polynomial time question):
非确定多项式时间问题,简称 NP 问题,就是能在多项式时间验证答案正确与否的问题。
简单的理解是NP问题算起来不一定快,但对于任何答案我们都可以快速的验证这个答案对不对。
2.3.举例理解NP问题-TSP旅行商推销问题
最著名的 NP 问题是TSP旅行商推销问题。
题目是在以下条件下,求出访问所有城市的最短路径
- 推销商有N个目的地城市
- 他需要访问所有城市一次,即不能重复
- 任意两座城市都是连接的,距离已知,即对应有权完全图
分析:
解决这个问题如果单纯的用枚举法来列举的话会有(n−1)!(n-1)!(n−1)! 种,已经不是多项式时间的算法了。将会是N的阶乘的复杂度O(n!)O(n!)O(n!)。
但是有快捷的方法,可以用猜的,假设人品爆炸猜几次就猜中了一条小于长度a的路径,TSP问题解决了,皆大欢喜。
可是,我不可能每次都猜的那么准,也许我要猜完所有种方案呢?
所以我们说,这是一个NP类问题。也就是这个问题能在多项式的时间内验证并得出问题的正确解,可是我们却不知道该问题是否存在一个多项式时间的算法,每次都能解决他(注意,这里是不知道,不是不存在,即能解决,但是无法找到一个多项式时间的算法的通解)。
- 其他NP问题:
Edge Cover 边覆盖
Set Cover 集合覆盖
Steiner Tree(Forest) 斯坦纳树
Max cut 最大割
SAT 可满足性
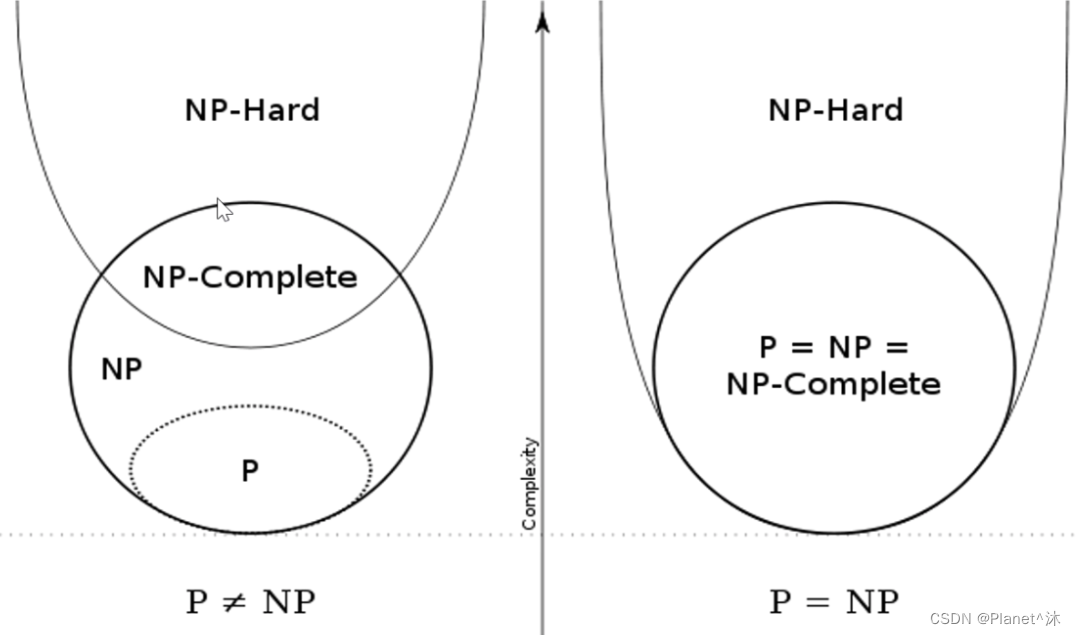
三、NP-hard问题&NP-C问题
3.1.NP-hard问题
- NP-hardness问题:
任意 NP 问题都可以在多项式时间内归约为一类问题,这类问题就称为 NP-hard 问题,这是比所有的NP问题都难的问题。
归约的意思是为了解决问题A,先将问题A归约为另一个问题B,解决问题B同时也间接解决了问题A。
3.2. NP-C问题
- NP-Complete问题:
但若所有的NP问题都能多项式归约到一类问题X,则称X为NP-hard问题,进一步如果X是NP的,称X是NP complete的。
换句话说,只要解决了这个问题,那么所有的NP问题都解决了。其定义要满足2个条件:一是NP-hard的问题,二是NP问题。
四、P&NP的联系
4.1. 理想:NP问题 = P问题
NP=PNP=PNP=P 意思是,如果对于一个问题能在多项式时间内验证其答案的正确性,那么是否能在多项式时间内解决它。
因为如果将所有的NP问题都 多项式规约 到某一个NP Complete问题,且只要一个NP Complete问题能在多项式时间内得到解决的话,那么所有的NP问题都可以在多项式时间内得到解决了。这个问题的解决将会带来世界性的进步。
4.2.现实:我们仍然相信 P问题!=NP问题
P≠NPP {\not=} NPP=NP
至今并没有人能证明某个NP Complete问题是P的。而且目前主流的观点是P不等于NP,当然这也没有确切的证明。如左图所示。