代码随想录算法训练营day47

思路：本题和上题的最多两次买卖相比，改成了最多k次，使用类似思路，需要设计1+2k个状态，第一个不设置也可以。dp五部曲：dp数组，dp[i][0-2k]，dp[i][0]表示无操作，dp[i][1]表示第一次持有的最大现金，dp[i][2]表示第一次不持有…dp[i][2k-1]表示第k次持有，dp[i][2k]表示第k次不持有；递推公式，类似上题，第i天第j次持有时，考虑第i-1天持有或不持有，dp[i][2j-1]=max(dp[i-1][2j-1],dp[i-1][2j-2]-prices[i])，第i天第j次不持有时，dp[i][2j]=max(dp[i-1][2j],dp[i-1][2j-1]+prices[i])；初始化，首先全部初始化为0，dp[i][0]始终为0，然后dp[0][2j-1]初始化为-prices[0]，dp[0][2j]初始化为0，类似上题；遍历顺序，顺序遍历；举例略。时间复杂度O(nk)。

class Solution {
public:int maxProfit(int k, vector<int>& prices) {vector<vector<int>> dp(prices.size(),vector<int>(2*k+1,0));for(int j=0;j<k;j++){//初始化dp[0][2*j+1]=-prices[0];}for(int i=1;i<prices.size();i++){for(int j=1;j<=k;j++){//第j次持有和第j次不持有dp[i][2*j-1]=max(dp[i-1][2*j-1],dp[i-1][2*j-2]-prices[i]);dp[i][2*j]=max(dp[i-1][2*j],dp[i-1][2*j-1]+prices[i]);}}return dp[prices.size()-1][2*k];}
};

注意cpp中数字和字母之间的乘号不能省略！否则报错。

思路：本题可以多次买卖，加入了一天冷冻期，卖出后第二天不能买，需要仔细分析状态，有四个状态，状态一为持有股票，然后对于不持有股票的情况，要分开讨论，状态二为保持卖出股票（两天前就卖掉了已经度过冷冻期，或者一直就没操作），即可以随时买入股票，度过了冷冻期，状态三为当天卖出股票，状态四为冷冻期，即前一天卖出股票。如图所示：

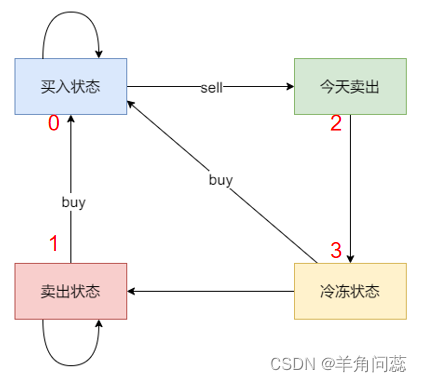
和前几题相比，本题增加了一个今天卖出股票的状态，之前都没有，因为冷冻期之前一天只能是当天卖出的状态，需要和普通的不持有股票状态区分开来。dp五部曲：dp数组：dp[i][0-4]分别表示持有股票、保持卖出股票、当天卖出股票、冷冻期的最大现金；递推公式：dp[i][0]，持有股票，前一天有三种情况，首先是本来就持有的dp[i-1][0]，然后是冷冻状态或者保持卖出状态下买入，dp[i-1][1]-prices[i]，dp[i-1][3]-prices[i]，取max，dp[i][1]卖出状态，前一天要么本来就是保持卖出，dp[i-1][1]，或者冷冻状态，dp[i-1][3]，取max，注意不是当天卖的，故不需要+prices[i]，dp[i][2]当天卖出，前一天必定是持有，dp[i][2]=dp[i-1][0]+prices[i]，dp[i][3]冷冻期，前一天必定是卖出股票，dp[i][3]=dp[i-1][2]；初始化，首先全部初始化为0，dp[0][0]=-prices[i]，dp[0][1]直接思考想不出设置为什么合适，所以直接根据递推公式算，经过几次递推后必定为0，dp[0][2]和dp[0][3]也为0；遍历顺序，顺序遍历；举例略。时间复杂度O(n)。最后返回值为状态1,2,3取max。

class Solution {
public:int maxProfit(vector<int>& prices) {vector<vector<int>> dp(prices.size(),vector<int>(4,0));dp[0][0]=-prices[0];for(int i=1;i<prices.size();i++){dp[i][0]=max(dp[i-1][0],max(dp[i-1][1]-prices[i],dp[i-1][3]-prices[i]));dp[i][1]=max(dp[i-1][1],dp[i-1][3]);dp[i][2]=dp[i-1][0]+prices[i];dp[i][3]=dp[i-1][2];}return max(dp[prices.size()-1][1],max(dp[prices.size()-1][2],dp[prices.size()-1][3]));}
};

思路：本题又是无限次交易，只不过添加了手续费，因此比较容易，只需要在交易的时候计算现金的时候减去手续费就OK。dp五部曲：dp数组，dp[i][0]表示持有股票最大现金，dp[i][1]表示不持有股票最大现金；递推公式，dp[i][0]=max(dp[i-1][0],dp[i-1][1]-prices[i]-fee)，对于交易手续费，我们在买的时候扣除就行了，dp[i][1]=max(dp[i-1][1],dp[i-1][0]+prices[i])；初始化，dp[0][0]=-prices[i]-fee，其他都初始化为0；遍历顺序，顺序遍历；举例略。时间复杂度O(n)。手续费在卖的时候扣也可以。

class Solution {
public:int maxProfit(vector<int>& prices, int fee) {vector<vector<int>> dp(prices.size(),vector<int>{0,0});dp[0][0]=-prices[0]-fee;for(int i=1;i<prices.size();i++){dp[i][0]=max(dp[i-1][0],dp[i-1][1]-prices[i]-fee);dp[i][1]=max(dp[i-1][1],dp[i-1][0]+prices[i]);}return dp[prices.size()-1][1];}
};