当前位置：首页 > news >正文

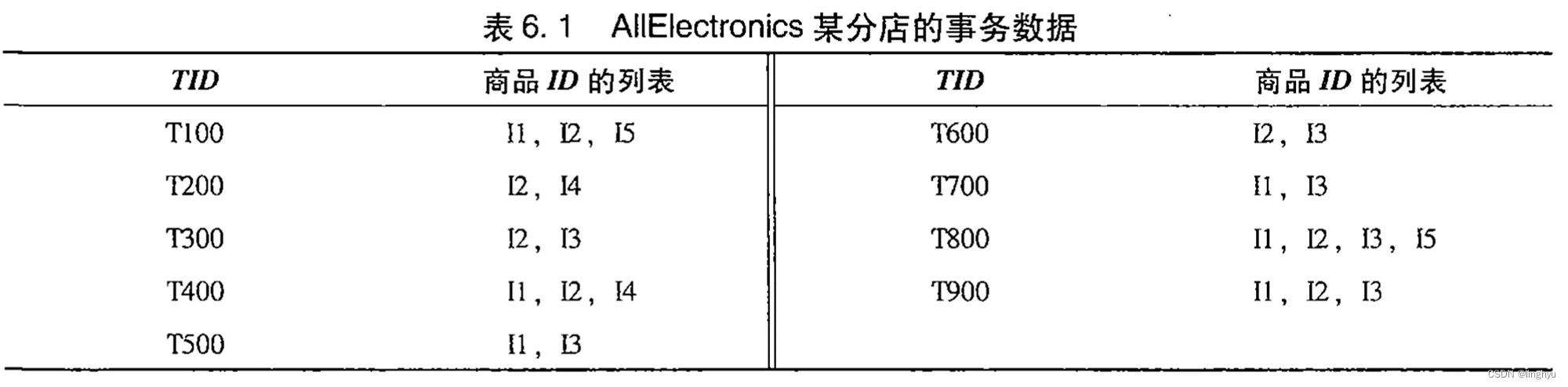
Apriori 处理ALLElectronics事务数据

news 2025/7/6 1:11:03

通过Apriori算法挖掘以下事务集合的频繁项集：

流程图

代码

# 导入必要的库
from itertools import combinations# 定义Apriori算法函数
def apriori(transactions, min_support, min_confidence):# 遍历数据，统计每个项的支持度 item_support = {}for transaction in transactions:for item in transaction:if item not in item_support:item_support[item] = 0item_support[item] += 1# 计算总事务数total_transactions = len(transactions)# 计算频繁项集frequent_itemsets = {}for item, support in item_support.items():if support / total_transactions >= min_support: # 即该项集在事务数据库中出现的次数除以总数frequent_itemsets[(item,)] = support / total_transactions# 生成候选项集并迭代生成频繁项集k = 2while True:candidates = set() # 存储所有可能的项集for itemset in frequent_itemsets.keys():for item in itemset:candidates.add(item)# 生成候选项集candidates = list(combinations(candidates, k)) # 生成所有可能的k项集# 统计候选项集的支持度candidate_support = {}for transaction in transactions:for candidate in candidates:if set(candidate).issubset(set(transaction)):if candidate not in candidate_support:candidate_support[candidate] = 0candidate_support[candidate] += 1# 更新频繁项集frequent_itemsets_k = {}for candidate, support in candidate_support.items():if support / total_transactions >= min_support:frequent_itemsets_k[candidate] = support / total_transactions# 如果没有频繁项集则停止迭代if not frequent_itemsets_k:breakfrequent_itemsets.update(frequent_itemsets_k)k += 1# 生成关联规则rules = []for itemset in frequent_itemsets.keys():if len(itemset) >= 2:for i in range(1, len(itemset)):for combination in combinations(itemset, i):X = combinationY = tuple(set(itemset) - set(combination))confidence = frequent_itemsets[itemset] / frequent_itemsets[X]if confidence >= min_confidence:rules.append((X, Y, frequent_itemsets[itemset], confidence))# frequent_itemsets (dict): 频繁项集和对应的支持度，键为项集的元组，值为支持度# rules (list): 关联规则，每一条规则表示为一个元组 (X, Y)，其中X为前项集合，Y为后项集合return frequent_itemsets, rules# 示例数据集
transactions = [    ['I1', 'I2', 'I5'],['I2', 'I4'],['I2', 'I3'],['I1', 'I2', 'I4'],['I1', 'I3'],['I2', 'I3'],['I1', 'I3'],['I1', 'I2', 'I3', 'I5'],['I1', 'I2', 'I3']
]
# 设置最小支持度和最小置信度阈值
min_support = 0.3
min_confidence = 0.6
# 调用Apriori算法函数
frequent_itemsets, rules = apriori(transactions, min_support, min_confidence)
print("频繁项集和对应的支持度：")
for itemset, support in frequent_itemsets.items():print("{}: Support = {:.2f}".format(itemset, support))
# 输出关联规则和置信度
print("\n关联规则和置信度：")
for X, Y, support, confidence in rules:print("{} => {}: Support = {:.2f}, Confidence = {:.2f}".format(X, Y, support, confidence))