【机器学习 复习】第9章 降维算法——PCA降维
一、概念
1.PCA
(1)主成分分析(Principal ComponentAnalysis,PCA)一种经典的线性降维分析算法。
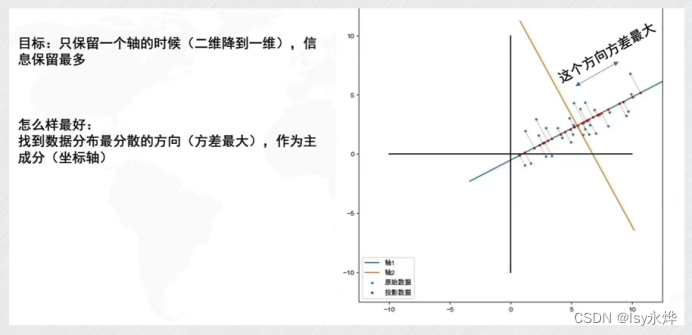
(2)原理,这里以二维转一维为例,原来的平面变成了一条直线
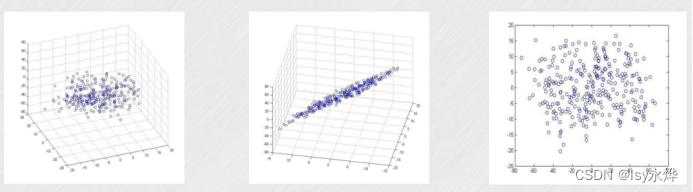
这是三维变二维:
(3)方差越大,特征的重要程度越大;方差越小,特征的重要程度越小。
如上面的例子中,样本集合中的数据在旋转过后的新的y轴上的方差接近于0,几乎不携带任何信息量,故可将其省去,达到降维的目的。
(所谓找方差最大的方向,就是找长度,面积最大的那条线或者面,因为方差就是离散程度,就是分散程度)
(4)降维对数据的处理主要包含特征筛选和特征提取。
前者是裁员,后者排列组合。
2.实际问题往往需要研究多个特征,而这些特征存在一定的相关性。
(1)数据量增加了问题的复杂性。
(2)将多个特征综合为少数几个代表性特征:
(3)既能够代表原始特征的绝大数信息,组合后的特征又互不相关,降低相关性。
(4)PCA是一种掌握事物主要矛盾的统计分析方法,它可以从多元事物中解析出主要影响因素,揭示事物的本质,简化复杂的问题。
3.方差贡献率:
(1)具体量化保留几个主成分往往根据实际情况通过计算累计方差贡献率来决定。
(2)方差的方差贡献率又称为解释方差(explained variance),
(人话就是说这个成分有多大用处)
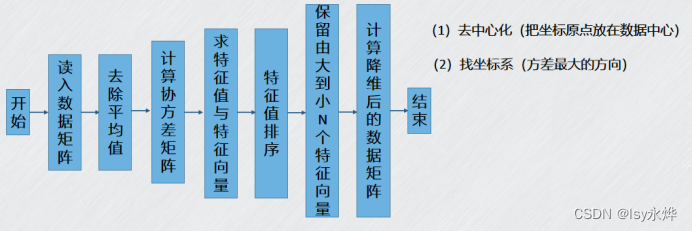
3.PCA算法步骤:
(1)用特征值表示哪个重要,越大越重要。
(2)特征值是由协方差矩阵求得。
(3)协方差就是数据相关程度,接近1是正相关,接近-1是负相关,0是不相关。
二、习题
单选题
3. 以下属于典型的监督学习的是( C)
A、聚类
B、关联分析
C、分类
D、降维
18. 以下属于典型的无监督学习的是(C)
A、支持向量机
B、k-近邻算法
C、降维
D、逻辑回归
判断题
2. 降维、聚类是无监督学习算法。(P)
16. 降维的目的就是降低数据的维度从而方便后续对数据的储存、可视化、建模等操作。(P)
17. 特征提取是指对现有特征进行重新组合产生新的特征,例如相对于年龄,出生年月就是冗余特征。(Í)
裁员是特征筛选
18. 对于n维特征变量中的每个子变量,主成分分析使用样本集合中对应子变量上取值的方差来表示该特征的重要程度。方差越小,特征的重要程度越高;方差越大,特征的重要程度越低。(Í)
方差越大,特征的重要程度越大;方差越小,特征的重要程度越小。