模式分解算法-满足3NF的无损且保持函数依赖的分解算法、满足BCNF的无损连接分解算法
一、引言
1、对指定的关系模式,若范式级别较低,为第一范式或第二范式,由于存在数据冗余或更新异常问题,在实际中一般是不可用的,关系模式的规范化就是将满足低一级的关系模式分解为若干满足高一级范式的关系模式的集合
2、在函数依赖范围内,希望分解消除数据冗余与操作异常等问题,得到的关系模式均能达到BCNF,并且分解具有无损连接性,同时分解保持函数依赖,但这三个目标有时不能同时满足,一般只能做到如下两点
(1)可以保证分解既具有无损连接性又保持函数依赖,但不能保证分解后的各关系模式属于BC范式,但可以都属于3NF
(2)可以保证分解后的各关系模式都属于BC范式,但只能保证分解再具有无损连接性,不能保证分解保持函数依赖
因此,在实际应用时应根据具体的需求来选择模式分解的方式
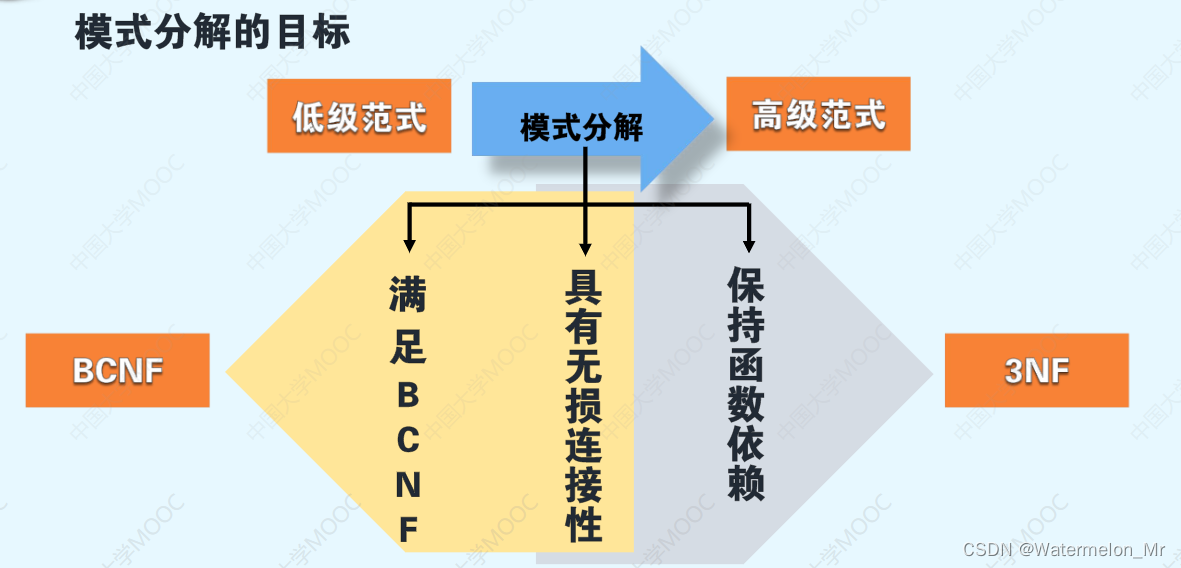
二、满足3NF的无损且保持函数依赖的分解算法
算法4:分解关系模式为满足3NF的一个无损且保持函数依赖的分解
1、输入、输出
输入:
关系模式R(U,F)
输出:
由R分解出的一个关系模式集合,
中每个关系模式属于3NF,且分解具有无损连接性并保持函数依赖关系模式集合
2、算法实现流程
(1)寻找F的最小函数依赖集,令
(2)对F中的函数依赖集按具有相同左部的原则分组,每一分组中的函数依赖集,所涉及的全部属性组成一个属性集
,若
,就去掉
(3)若均不包含R的候选键(此处说明必须求出R中所有的候选键),则增加一个只包含候选键的属性集
;
(4)将及F在
上的投影
构成分解
中的一个关系模式
3、举例:

分析:
(1)由于分解中的关系模式
中包含了R中的候选键,可用判断一个分解是否为无损连接分解的算法来验证分解
具有无损连接性,可验证结果表中包含候选键的关系模式所在的行一定可称为全a
(2)由于F是最小函数依赖集每个分组上的函数依赖的左部相同,分解中的每个关系模式
,一定是一个以函数依赖左部为码的3NF,即使对于
包含于
,
包含于
的情况,也只是在分解结果的
和
中,增加了主属性对于候选键的部分或传递函数依赖,因此
是所求分解
四、满足BCNF的无损连接分解算法
算法5:分解关系模式为满足BCNF的一个无损连接分解
1、输入和输出
输入:
关系模式R(U,F)
输出:
由R分解出的一个关系模式集合,
中每个挂你模式都属于BCNF,且分解具有无损连接性
2、递归算法实现流程:
(1)判断R是否属于BCNF,若是,则返回={R};
(2)R不属于BCNF,必有函数依赖,X不是R的候选键,计算
,将R分解为
和
,
;
(3)对F在和
进行投影,得到
和
;
(4)返回第(1)步,递归地分解和
,返回分解得到的结果集合。
3、举例:




分析:
因为在关系模式中,包含了R的一个候选键HS,利用判断一个分解是否是无损连接分解的算
法,可以验证该分解具有无损连接性
五、小结
(1)利用不同的模式分解算法可按不同的分解目标实现关系模式的规范化设计
(2)数据库设计者在设计关系数据库时,一般尽可能设计成BCNF模式集
