基于MATLAB仿真LFM线性调频信号
基于MATLAB仿真LFM线性调频信号
目录
前言
一、LFM信号简介
二、LFM信号基本原理
三、LFM信号仿真
四、代码
总结
前言
仿真中的接收信号,有时为了简单会直接用一个正弦波代替,但实际中接收到的信号极少是点频信号,一般都是PSK信号、OFDM信号、LFM信号等等。但最近想仿真一下LFM信号,将其用到自己某些算法的仿真中,于是有了下文。本文将详细介绍LFM的原理及展示用MATLAB仿真得到的LFM波形及频谱,当然,文末也有代码,感兴趣的伙伴可以下载验证。
提示:以下是本篇文章正文内容,希望能帮助到各位,转载请附上链接。
一、LFM信号简介
调频或调相信号可用来实现更宽的工作带宽。线性调频信号(Linear Frequency Modulation, LFM)是一种常见的调制方式,广泛应用于雷达、通信和声纳等领域。其特点有:
- 宽带特性:LFM信号的频谱范围较宽,可以在有限的时间内覆盖较宽的频带。
- 高分辨率:由于其宽带特性,LFM信号在雷达和声纳中可以提供高的距离分辨率和速度分辨率。
- 良好的抗干扰能力:LFM信号具有较好的抗干扰能力和低可检测性。
LFM信号的时间带宽积近似,其中B为信号带宽,
为脉冲宽度。
二、LFM信号基本原理
LFM信号,频率线性地向上(上线性调频)或向下(下线性调频)扫过脉冲宽度。
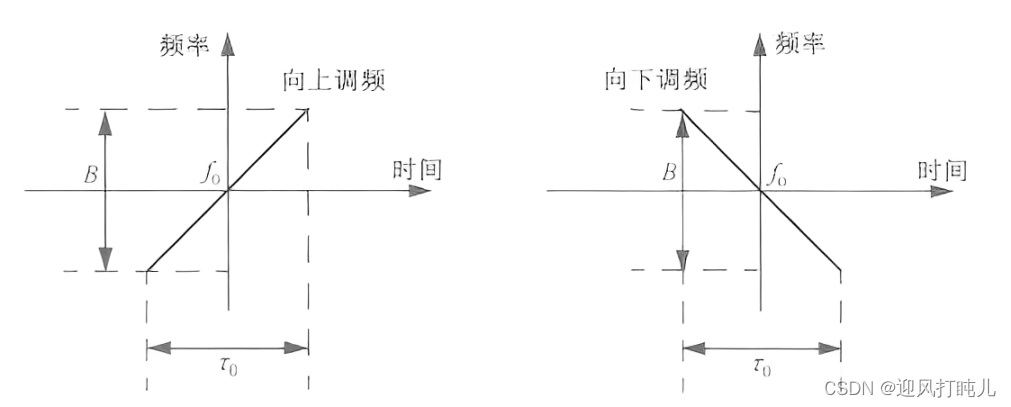
向上线性调频瞬时相位可表示为:
式中,f0为雷达中心频率,是线性调频系数。因此,瞬时频率为
类似地,向下线性调频瞬时相位和频率分别为
典型线性调频波形可表示成
式中, 表示宽度为
的矩形脉冲。记住,信号
是线性调频波形的解析信号。由此可得
信号的谱由其复包络
确定。
的复指数项引入了一个关于中心频率
的频移。
三、LFM信号仿真
参数设置如下:
B = 100e6; %带宽
T = 10e-6; %脉冲宽度
Fs = 1e9; %采样频率
N = T*Fs+1; %采样点数
mu = B/T; %计算LFM系数
t = linspace(-T/2,T/2,N); %确定采样时刻
下面分别是线性调频波形实部、虚部和频谱图的曲线。
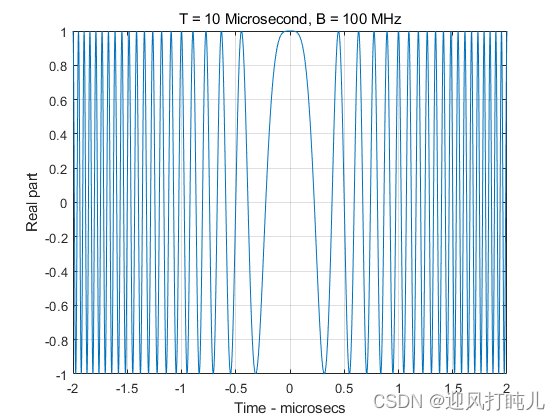
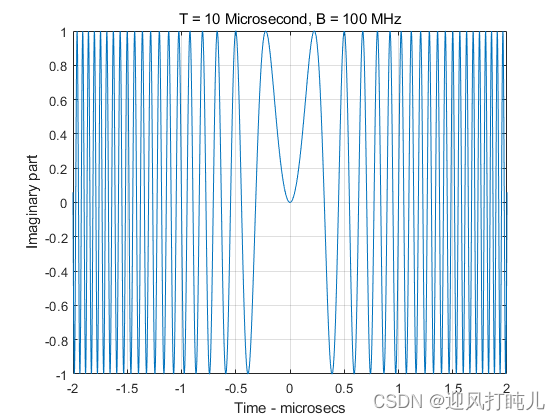
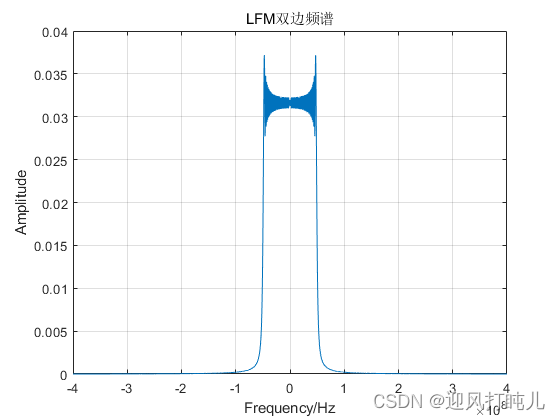
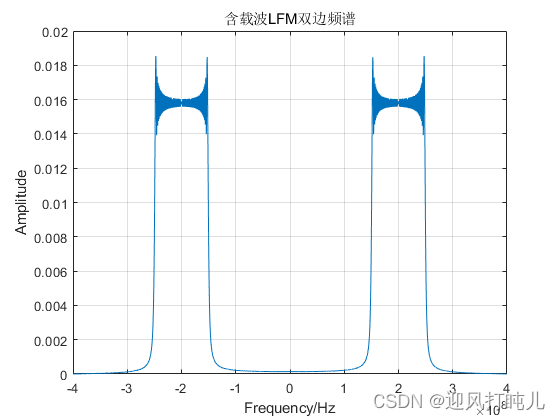
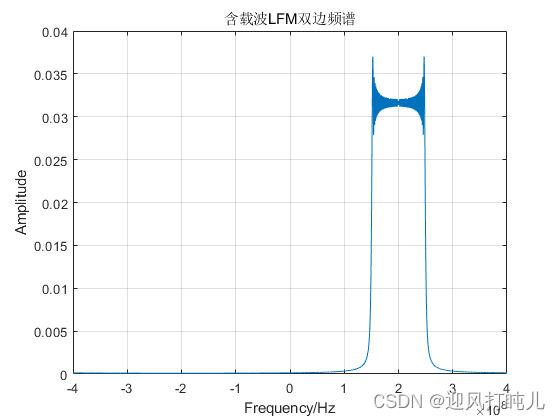
若带有载波,设置载波为200MHz(这里载波设置的较小,仅仅为了查看频谱图的效果),则LFM的频谱图如下所示:
载波为cos(2*pi*f0*t)
载波为exp(1j*2*pi*f0*t)
四、代码
https://download.csdn.net/download/m0_66360845/89469669![]() https://download.csdn.net/download/m0_66360845/89469669
https://download.csdn.net/download/m0_66360845/89469669
总结
以上就是今天要分享的全部内容,本文详细介绍了LFM信号的原理,还提供了基于MATLAB的LFM信号的仿真波形,希望对读者有所帮助。
