【SCAU数据挖掘】数据挖掘期末总复习题库应用题及解析
1.
给定圆的半径为e ,令 MinPts=3,考虑下面两幅图。
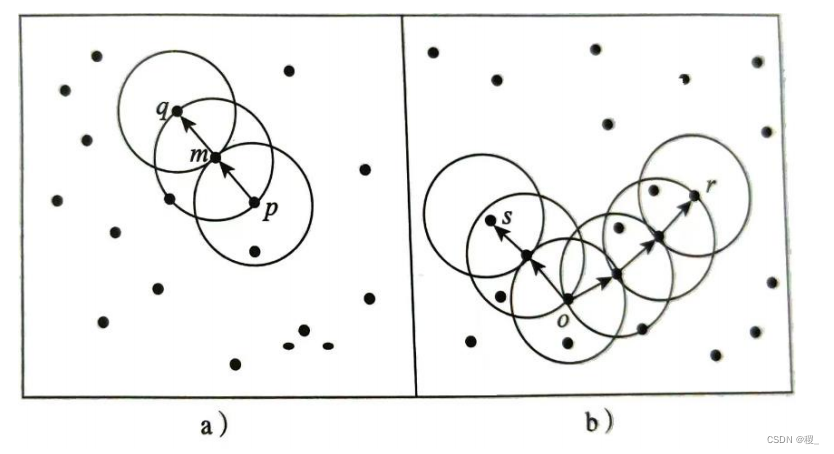
(1)哪些对象是核心对象?
m,p,o,r(因为这些核心对象在半径e的范围内都至少包含MinPts=3个对象)
(2)哪些对象是直接密度可达的?
对象q是从m直接密度可达的。对象m从p直接密度可达的。
(3)哪些对象是密度可达的?
对象q是从p(间接)密度可达的(因为q从m直接密度可达,m从p直接密度可达。)
r和s是从o密度可达的
(4)哪些对象是密度相连的?
r和s是从o密度可达的,所以r和s是密度相连的。
核心对象:如果一个对象的ε-邻域内至少包含MinPts个对象,则该对象为核心对象。在这里,ε是邻域半径,MinPts是给定的最小点数。
直接密度可达:如果对象p在对象q的ε-邻域内,且q是核心对象,那么对象p从对象q出发是直接密度可达的。
密度可达:如果存在一个对象链p1, p2, ..., pn,其中p1=q,pn=p,且pi+1从pi关于ε和MinPts直接密度可达,那么对象p从对象q出发是密度可达的。
密度相连:如果对象集合D中存在一个对象o,使得对象p和q都是从o关于ε和MinPts密度可达的,那么对象p和q是关于ε和MinPts密度相连的。
2.相异性计算
给定两个元组(22,1,42,10)和(20,0,36,8):
(1)计算这两个对象之间的欧几里得距离。
(2)计算这两个对象之间的曼哈顿距离。
(3)使用q=3,计算这两个对象之间的闵可夫斯基距离。
(4)计算这两个对象之间的上确界距离。
欧几里得距离(Euclidean Distance):两点之间的直线距离
曼哈顿距离(Manhattan Distance):是两点在标准坐标系上的绝对轴距总和
上确界距离(Supremum Distance):是两点在各维度上距离的最大值
(1)![]()
d=sqrt((22-20)^2+(1-0)^2+(42-36)^2+(10-8)^2)=sqrt(45)
(2)![]()
d=∣22−20∣+∣1−0∣+∣42−36∣+∣10−8∣=2+1+6+2=11
(3)d=max(|p-q|)=6
(4)![]()
d=max(∣22−20∣,∣1−0∣,∣42−36∣,∣10−8∣)=max(2,1,6,2)=6
3.
对于数据:{12,9,7,6,20,100,35,21,11,18,25,37},完成以下任务:
(1)计算它的平均值,20%的截断均值和中位数,并说明这三个统计特征在描述数据集方面的特点。
(2)使用最小-最大规范方法将其中的6,100,35转换到[0,1]。
(1)
平均值 = (12 + 9 + 7 + 6 + 20 + 100 + 35 + 21 + 11 + 18 + 25 + 37) / 12 = 25.08
20%截断均值:12×0.2=3.6向上取整到4个
首先将数据从小到大排序: {6, 7, 9, 11, 12, 18, 20, 21, 25, 35, 37, 100}
去掉最小的2个和最大的2个
{9, 11, 12, 18, 20, 21, 25, 35}
20%截断均值 = (9 + 11 + 12 + 18 + 20 + 21 + 25 + 35) / 8 = 18.875
中位数(18+20)/2=19
(2)
最小-最大规范化:将待转换数据减去最小值,再除以极差(最大值-最小值)
原数据集中最小值为6,最大值为100
极差 = 100 - 6 = 94
6的规范化值 = (6 - 6) / 94 = 0
100的规范化值 = (100 - 6) / 94 = 1
35的规范化值 = (35 - 6) / 94 = 0.3085
所以6、100、35分别规范化为0、1、0.3085
4.
对于如下的前馈神经网络,假设现在有一个训练样本,X={1,0,1},其对应的类标号(标签)为1,节点4、5、6的激活函数为sigmoid函数,结构如下图所示:

网络的初始输入、权值(w)和偏置值(4、5、6节点分别为![]() 、
、![]() 、
、![]() )如下表所示:
)如下表所示:

(1)请计算节点4、5、6的净输入![]() 和输出
和输出![]() 。
。

(2)请计算节点4、5、6的误差![]() 。
。

(3)假设学习率为0.9,请计算上表中所有权值和偏置的一次更新。
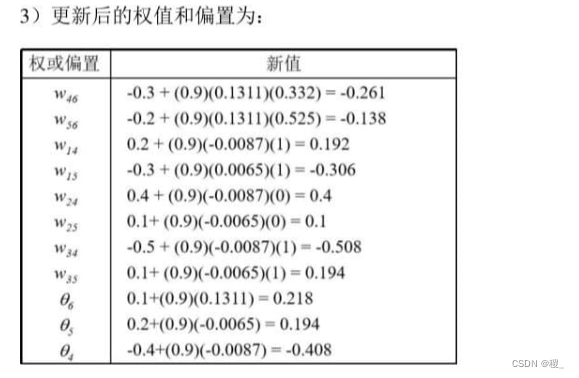
(4)请问什么是梯度消失?

