第五十一天 | 1143.最长公共子序列
题目:1143.最长公共子序列718.最长重复子数组的区别是,子序列不要求连续,子数组要求连续。这一差异体现在dp数组含义和递推公式中,本题是子序列,那就要考虑上nums1[i - 1] != nums2[j - 1]的情况。
本道题与
1.dp数组含义:
dp[i][j]:本题是子序列,那么dp数组的含义是长度为[0, i - 1]的字符串text1与长度为[0, j - 1]的字符串text2的最长公共子序列为dp[i][j]。上一题是子数组,那么dp数组的含义是以dp[i - 1]和dp[j - 1]结尾的最长的重复子数组
这样定义是为了后面代码实现方便,如果非要定义为长度为[0, i]的字符串text1也可以,我在 动态规划:718. 最长重复子数组 (opens new window)中的「拓展」里 详细讲解了区别所在,其实就是简化了dp数组第一行和第一列的初始化逻辑。
2.递推公式:
主要就是两大情况: text1[i - 1] 与 text2[j - 1]相同,text1[i - 1] 与 text2[j - 1]不相同
如果text1[i - 1] 与 text2[j - 1]相同,那么找到了一个公共元素,所以dp[i][j] = dp[i - 1][j - 1] + 1;
如果text1[i - 1] 与 text2[j - 1]不相同,那就看看text1[0, i - 2]与text2[0, j - 1]的最长公共子序列 和 text1[0, i - 1]与text2[0, j - 2]的最长公共子序列,取最大的。
即:dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
3.dp数组如何初始化
先看看dp[i][0]应该是多少呢?
test1[0, i-1]和空串的最长公共子序列自然是0,所以dp[i][0] = 0;
同理dp[0][j]也是0。
其他下标都是随着递推公式逐步覆盖,初始为多少都可以,那么就统一初始为0。
4.确定遍历顺序
从递推公式,可以看出,有三个方向可以推出dp[i][j],如图:
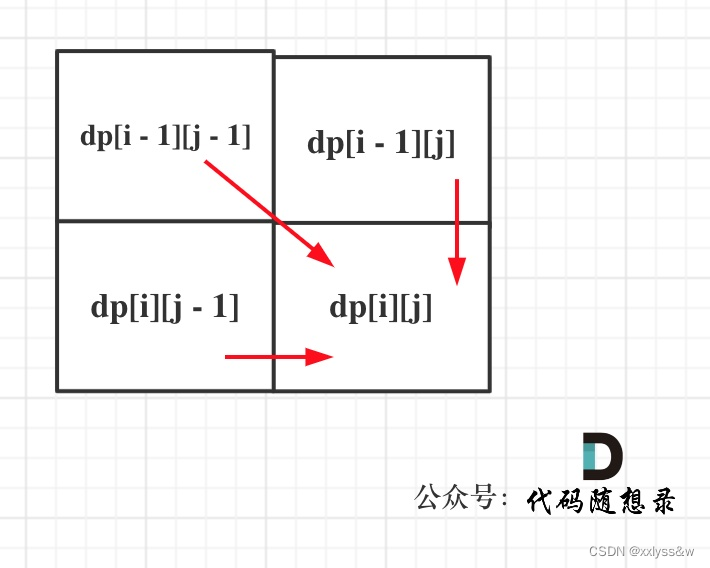
那么为了在递推的过程中,这三个方向都是经过计算的数值,所以要从前向后,从上到下来遍历这个矩阵
dp[text1.size()][text2.size()]为最终结果
class Solution:def longestCommonSubsequence(self, text1: str, text2: str) -> int:dp = [[0] * (len(text2) + 1) for _ in range (len(text1) + 1)]for i in range(1, len(text1) + 1):for j in range(1, len(text2) + 1):if text1[i - 1] == text2[j - 1]:dp[i][j] = dp[i - 1][j - 1] + 1else: dp[i][j] = max(dp[i][j - 1], dp[i - 1][j])return dp[len(text1)][len(text2)]