PyTorch -- 最常见激活函数的选择
-
首先,简单复习下什么是梯度:梯度是偏微分的集合
- 举例说明:对于 z = y 2 − x 2 : ∇ z = ( ∂ z ∂ x , ∂ z ∂ y ) = ( 2 x , 2 y ) z = y^2-x^2: \nabla z= (\frac{\partial z}{\partial x}, \frac{\partial z}{\partial y}) = (2x, 2y) z=y2−x2:∇z=(∂x∂z,∂y∂z)=(2x,2y)
-
获取极小值
minima的方法核心: θ t + 1 = θ t − α ∇ f ( θ t ) \theta_{t+1}=\theta_t-\alpha\nabla f(\theta_t) θt+1=θt−α∇f(θt)
-
【
torch.sigmoid()】 Sigmoid ( x ) = 1 1 + e − x \text{Sigmoid}(x)=\frac{1}{1+e^{-x}} Sigmoid(x)=1+e−x1
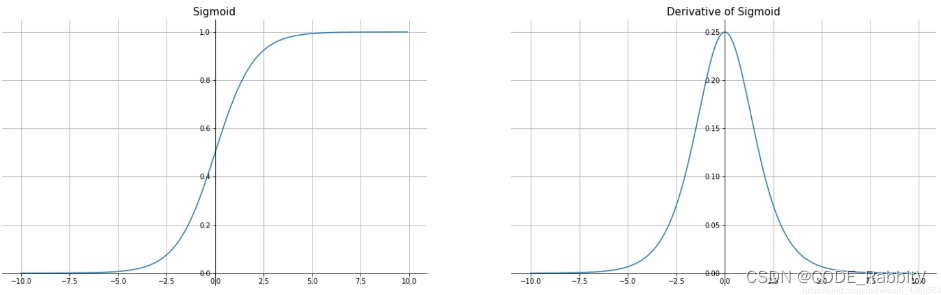
- 优点:连续函数,便于求导,可以用作输出层
- 缺点:在变量取
绝对值非常大时会出现饱和现象(函数会变得很平),且对输入的微小改变会变得不敏感;在反向传播时,当梯度接近于0,容易出现梯度消失,从而无法完成深层网络训练
-
【
torch.tanh()】 Tanh ( x ) = e x − e − x e x + e − x \text{Tanh}(x) = \frac{e^x-e^{-x}}{e^x+e^{-x}} Tanh(x)=ex+e−xex−e−x

- 优点:同 sigmoid 且均值是0 (更好)
- 缺点:仍存在
饱和问题
-
【
torch.relu()】 ReLU ( x ) = max ( 0 , x ) \text{ReLU}(x)=\max(0,x) ReLU(x)=max(0,x)
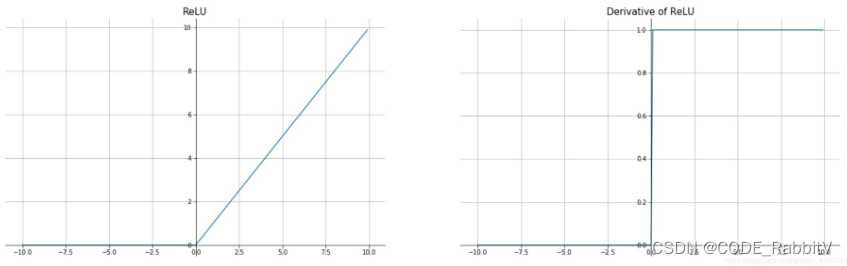
- 优点:高效;在x>0区域上,不会出现梯度饱和、梯度消失
- 缺点:
Dead ReLU Problem(在x<0时,梯度为0:这个神经元及之后的神经元梯度永远为0,不再对任何数据有所响应,导致相应参数永远不会被更新)
- B站视频参考资料
