图的遍历介绍
概念
特点
无论是进行哪种遍历,均需要通过设置辅助数组标记顶点是否被访问来避免重复访问!!!!

类型

深度优先遍历
可以实现一次遍历访问一个连通图中的所有顶点,只要连通就能继续向下访问。
因此,深度递归次数就是图中连通分量数。
遍历过程
类似树的先根遍历,先访问结点,再访问与其邻接的第一个结点。

示例

遍历邻接矩阵表示图的实现
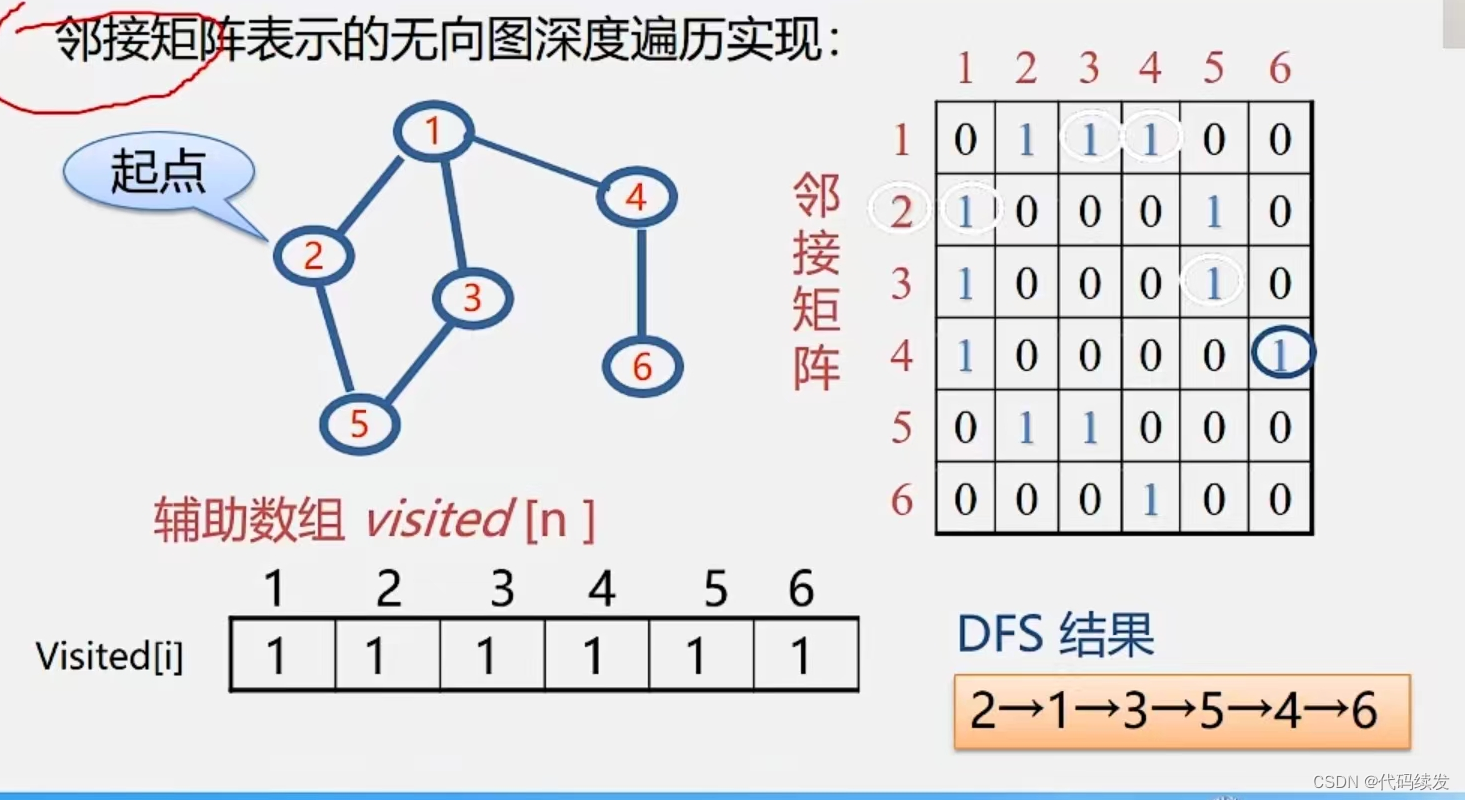

效率分析

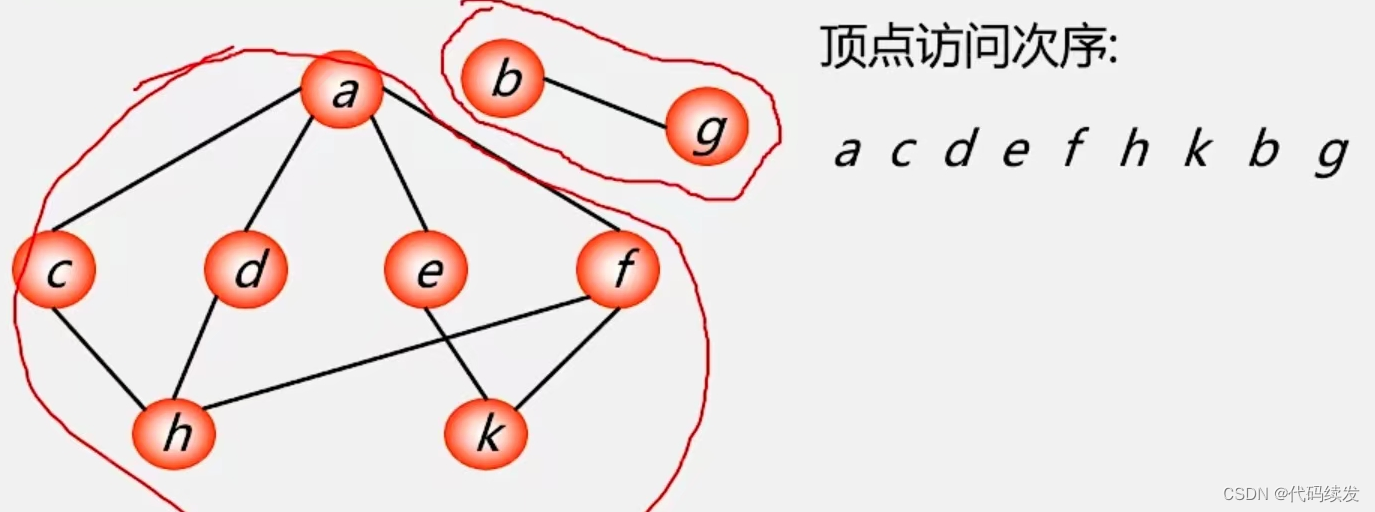
非连通图的遍历
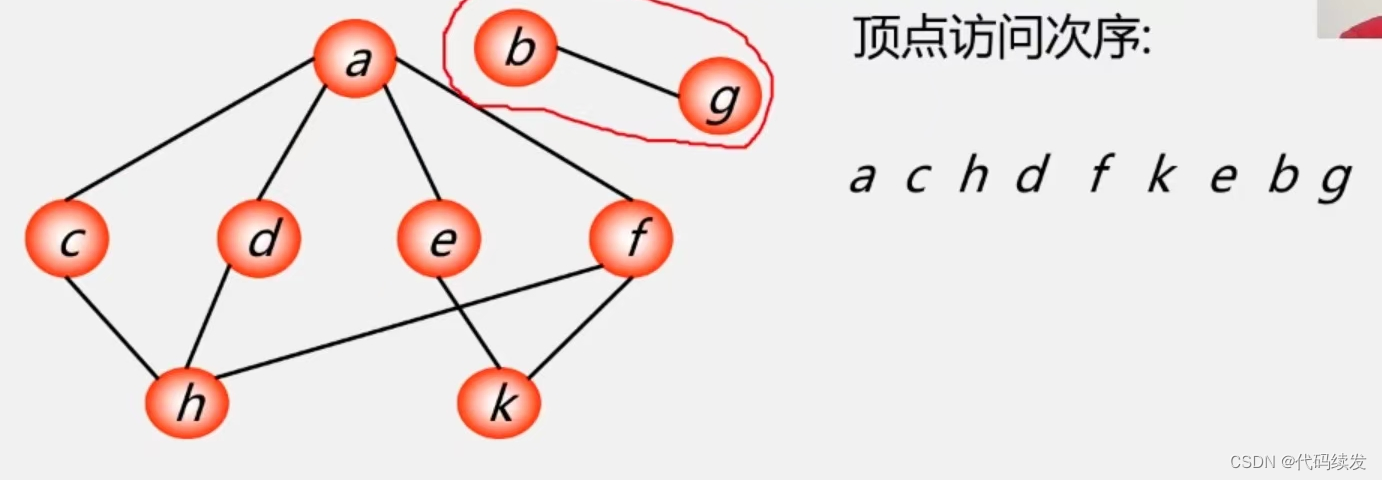
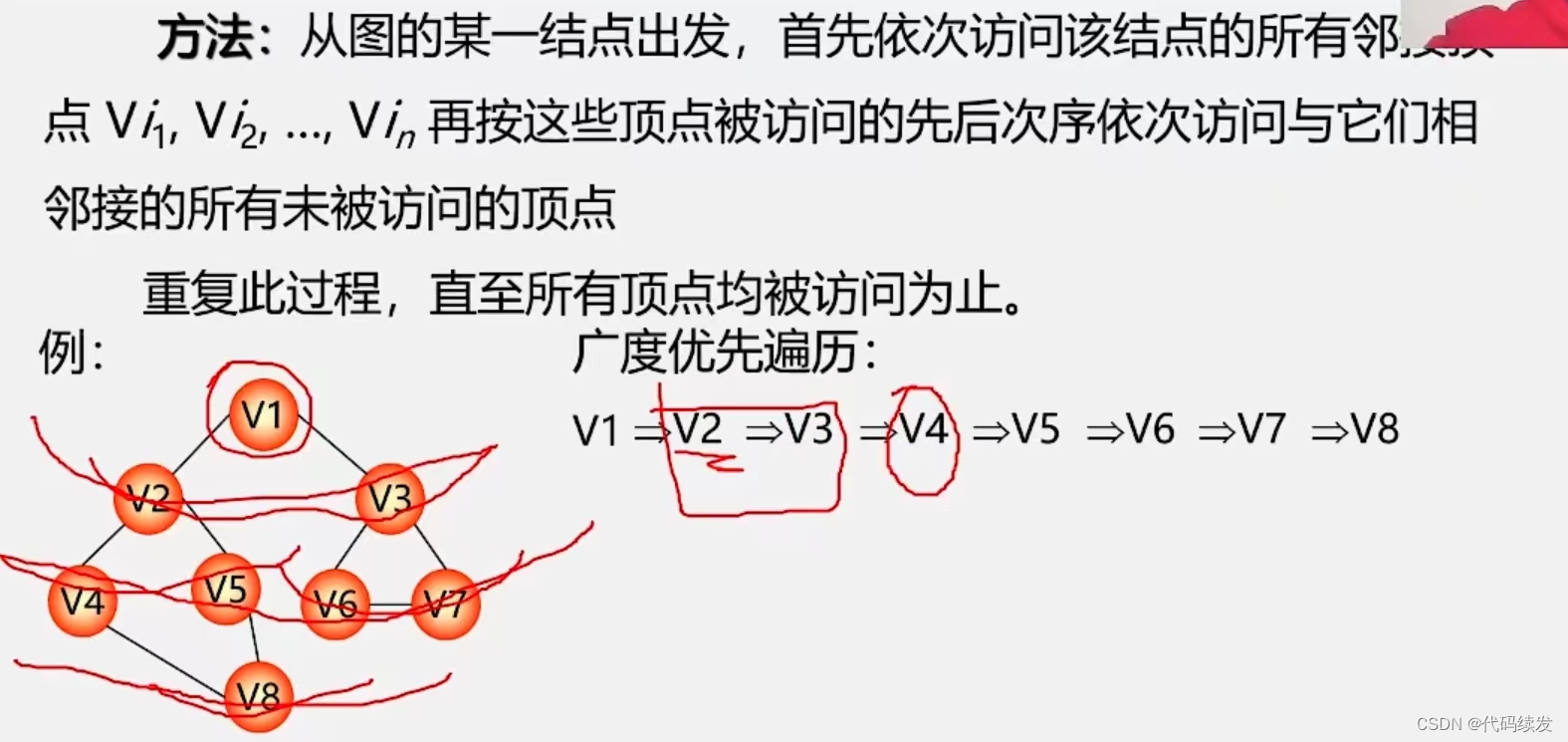
广度优先搜索
遍历过程
类似于树的层序遍历,先访问结点,再访问与结点邻接的所有结点。
非连通图的遍历
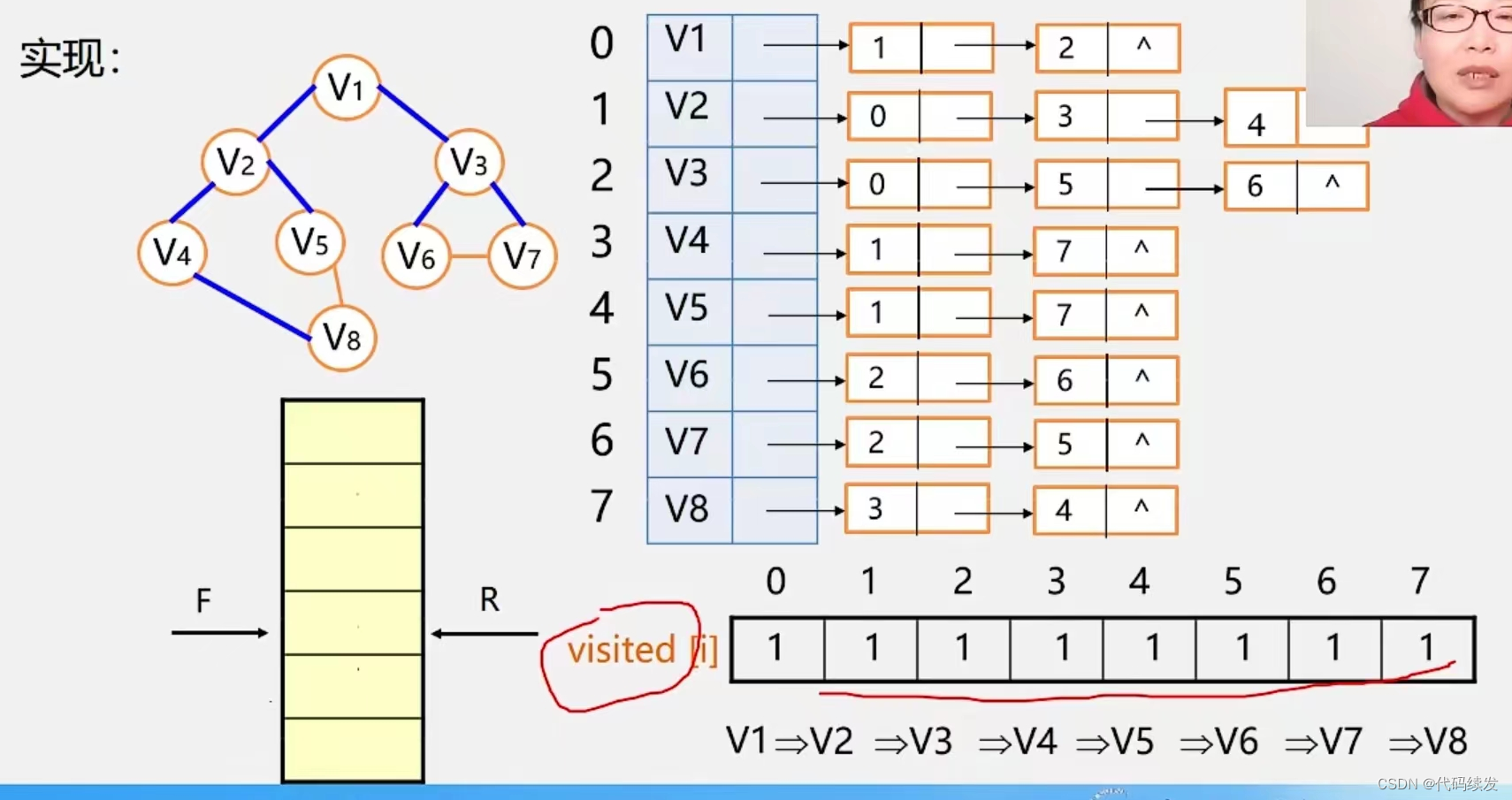
遍历邻接表表示图的实现

效率分析

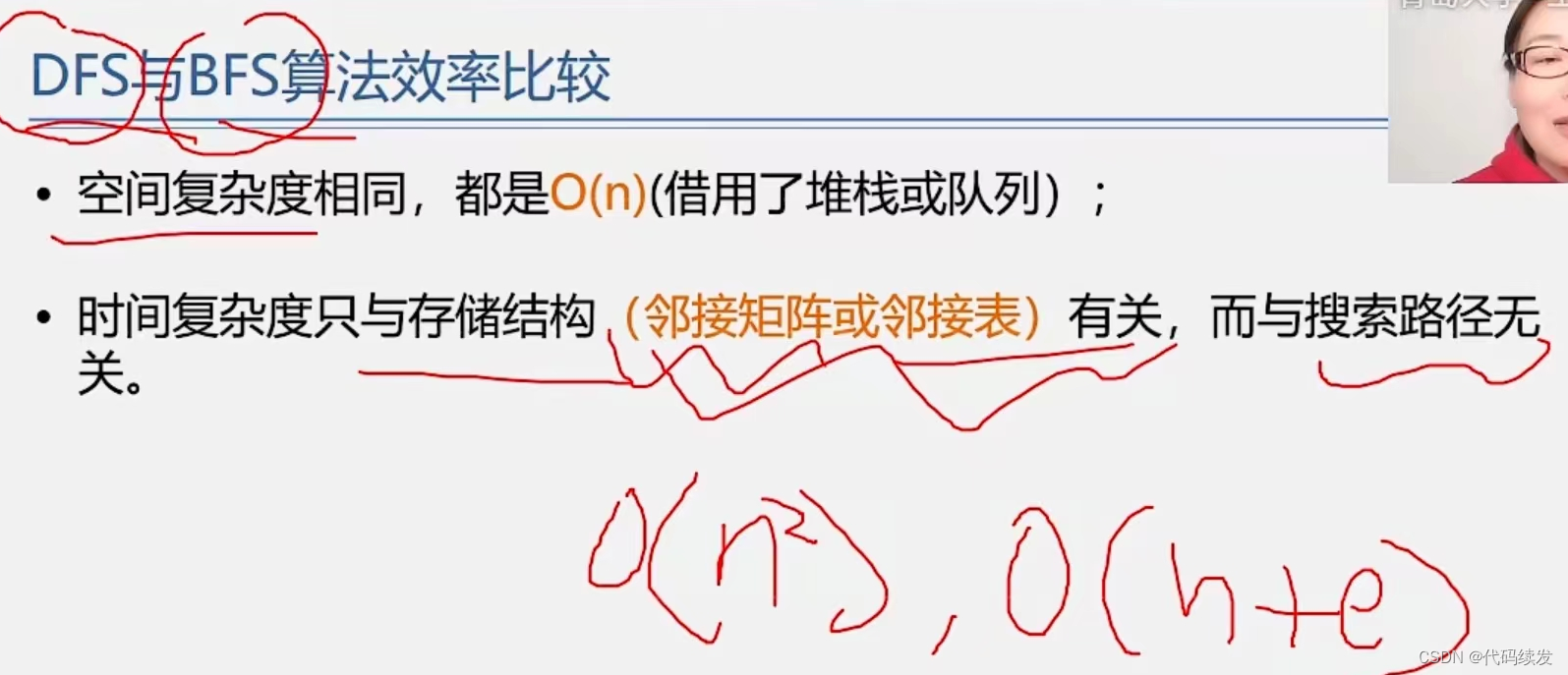
DFS其底层是借助一个递归工作栈实现的。
而BFS是借助一个辅助队列实现的。
时间复杂度只与存储结构有关!!!!!
代码整合
#include <iostream>
#define maxn 100
#define infi 333333
using namespace std;
int visit[maxn]={0};
//邻接矩阵:顶点数+边数+顶点表(一维)+边表(二维)
typedef struct node{int vnum,arcnum;char vexs[maxn];int acr[maxn][maxn];
}adjgraph;
//邻接表:顶点数+边数+顶点表==>顶点类型:顶点信息+第一条边==> 边类型:顶点编号+权值+下一条边
typedef struct acrnode{int num;int weigh;acrnode *nextacr;
}acrnode;
typedef struct vexnode{char vex;acrnode *firstacr;
}vexnode;
typedef struct node{int vnum,acrnum;vexnode vexs[maxn];
}listgraph;//深度遍历
//递归实现:传入图与起点,不断调用自身
//用邻接矩阵实现
void dfs1(adjgraph g,int v){ cout<<v<<endl;visit[v]=1;for(int i=0;i<g.vnum;i++){if(visit[i]==0&&acr[v][i]!=infi)dfs(g,i);}
}
//用邻接表实现
void dfs2(listgraph l,int v){acrnode edge;vexnode vex; cout<<v<<endl;visit[v]=1;for(edge=l.vexs[v].firstacr;edge;edge=edge.nextacr){//遍历与v相连的所有边-有边 vex=l.vexs;//记录结点if(!visit[vex]) //且未被访问 dfs(l,vex);//访问结点 }
}//非递归实现:通过栈实现
//1.初始栈和标志数组
//2.起点元素入栈,
//3.栈非空:出栈访问,遍历下一条邻接边,未被访问时入栈,取下一个邻接结点
stack<int> s
void dfs(adjgraph g,int v){//邻接矩阵实现 int t;initstack(s);push(s,v);while(!empty(s)){t=pop(s,v);if(!visit[t]){cout<<t<<endl;visit[t]=1;}for(int i=0;i<g.vnum;i++){if(g.arcnum[v][i]!=infi&&(!visit[i])){push(s,i);}}}
}//广度遍历
1.初始队列与标记数组
2.起点元素入队,
3.队非空:出队,遍历边,未被访问时访问入队
void bfs(listgraph l,int v) {//用队列实现acrnode w;cout<<v<<endl;visit[v]=1;init(q); enqueue(q,v);while(!isempty(q)) {dequeue(q,v);for(w=l.vexs[v].firstacr;w;w=w.nextacr)//遍历邻接的所有边 {if(!visit[w]){cout<<w<<endl;visit[w]=1;enqueue(q,w);}}}
}