当前位置：首页 > news >正文

MATLAB——DFT(离散傅里叶变换)

news 2025/9/12 10:24:19

题目1：
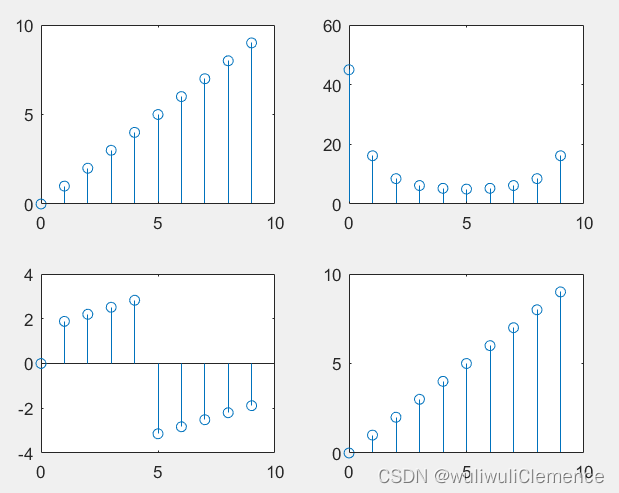
已知有限长序列x(n)为：
x(n)=[0,1,2,3,4,5,6,7,8,9]，求x(n)的DFT和IDFT。要求
1）画出序列傅里叶变换对应的|X(k)|和arg[X(k)]图形。
2）画出原信号与傅里叶逆变换IDFT[X(k)]图形进行比较。
知识点：
DFT（Discrete Fourier Transform）和IDFT（Inverse Discrete Fourier Transform）是互为逆运算的变换。

给定一个长度为 $N$ 的复数序列 $x0,x1,x2,…,xN−1x_0, x_1, x_2, \dots, x_{N-1}$ ，DFT 将其转换为另一个长度为 $N$ 的复数序列 $X0,X1,X2,…,XN−1X_0, X_1, X_2, \dots, X_{N-1}$ ：

$Xk=∑n=0N−1xne−j2πkn/N,k=0,1,2,…,N−1X_k=\sum_{n=0}^{N-1}x_n e^{-j2\pi kn/N}, \quad k=0,1,2,\dots,N-1$

IDFT 则将 $X0,X1,X2,…,XN−1X_0, X_1, X_2, \dots, X_{N-1}$ 转换回 $x0,x1,x2,…,xN−1x_0, x_1, x_2, \dots, x_{N-1}$ ：
$xn=1N∑k=0N−1Xkej2πkn/N,n=0,1,2,…,N−1x_n=\frac{1}{N}\sum_{k=0}^{N-1}X_k e^{j2\pi kn/N}, \quad n=0,1,2,\dots,N-1$
程序：
主要是根据变换公式来的，不要忘了逆变换要除以N，有了前面 DFS的基础，这个代码相对比较简单。

xn=[0,1,2,3,4,5,6,7,8,9];
N=length(xn);
n=0:N-1;
k=0:N-1;
WN=exp(-2*j*pi/N);XK=xn*WN.^(n'*k);
x=XK*WN.^(-n'*k)/N;
subplot(221);
stem(n,xn);
subplot(222);
stem(k,abs(XK));
subplot(223);
stem(k,angle(XK));
subplot(224);
stem(n,x);

运行结果：
在这里插入图片描述
题目2：
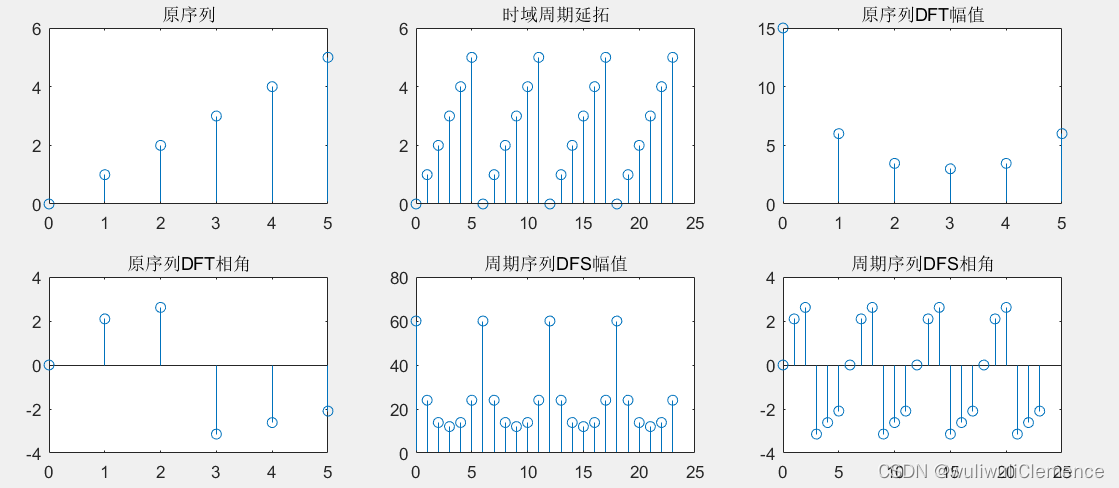
有限长序列DFT与周期序列DFS的联系
已知周期序列的主值x(n)=[0,1,2,3,4,5]，求x(n)周期重复次数为4次时的DFS。要求
1）画出原主值序列和信号周期序列；
2）画出序列傅里叶变换对的图形。
知识点：
我们知道，在时域上。周期序列可以看做是有限长序列的周期延拓。在频域上是否也这样呢。答案是肯定的，现在来进行验证。
代码：

x0=[0,1,2,3,4,5];
N0=length(x0);
n0=0:N0-1;
k0=0:N0-1;
x1=x0';%转置
xn=x1*ones(1,4);
xn=xn(:)';
NN=length(xn);
nn=0:NN-1;
kn=0:NN-1;
%nn=0:4*N0-1;   
%kn=0:4*N0-1;
%xn=x0(mod(nn,N0)+1);
subplot(231);
stem(n0,x0);
title('原序列');
subplot(232);
stem(nn,xn);
title('时域周期延拓');%求原序列的DFT
WN0=exp(-2*j*pi/N0);
X0K=x0*WN0.^(n0'*k0);
subplot(233);
stem(k0,abs(X0K));
title('原序列DFT幅值');
subplot(234);
stem(k0,angle(X0K));
title('原序列DFT相角');%延拓的DFS
WNN=exp(-2*j*pi/N0);
%一定要注意这个地方除N0，虽然进行了周期延拓，但是一个周期上的采样点数，没有变
XNK=xn*(WNN.^(nn'*kn));
subplot(235);
stem(kn,abs(XNK));
title('周期序列DFS幅值');
subplot(236);
stem(kn,angle(XNK));
title('周期序列DFS相角');
XN=dfs(xn,NN);