文章目录 一、多分类评估指标的 macro 和 weighted 过程 1. 多分类 F1-Score 评估指标 2. 多分类 ROC-AUC 评估指标 二、借助机器学习流构建全域参数搜索空间 三、优化评估指标选取 1. 高级评估指标的选用方法 2. 同时输入多组评估指标 四、优化后建模流程
在正式讨论关于网格搜索的进阶使用方法之前,我们需要先补充一些关于多分类问题的评估指标计算过程。 在此前的内容中,我们曾经介绍过分类模型在解决多分类问题时的不同策略,同时也介绍过二分类问题的更高级评估指标,如 F1-Score 和 ROC-AUC 等。 接下来我们将详细讨论关于多分类预测结果在 F1-Socre 和 ROC-AUC 中的评估过程,以及 在sklearn 中如何调用函数进行计算。
import numpy as np
import pandas as pd
import matplotlib as mpl
import matplotlib. pyplot as plt
from ML_basic_function import *
from sklearn. preprocessing import StandardScaler
from sklearn. preprocessing import PolynomialFeatures
from sklearn. linear_model import LogisticRegression
from sklearn. pipeline import make_pipeline
from sklearn. model_selection import GridSearchCV
from sklearn. model_selection import train_test_split
from sklearn. metrics import accuracy_score
from sklearn. datasets import load_iris
首先导入和 F1-Score 相关的评估指标计算函数。 from sklearn. metrics import precision_score, recall_score, f1_score
然后简单查看相关说明文档,发现这几组和混淆矩阵相关的评估指标基本是共用了一套参数命名,并且大多数参数其实都是作用于多分类问题,对于二分类问题,我们可以简单调用相关函数直接计算: y_true = np. array( [ 1 , 0 , 0 , 1 , 0 , 1 ] )
y_pred = np. array( [ 1 , 1 , 0 , 1 , 0 , 1 ] ) precision_score( y_true, y_pred) , recall_score( y_true, y_pred) , f1_score( y_true, y_pred)
precision_score?
Name Description y_true 数据集真实标签 y_pred 标签预测结果 labels 允许以列表形式输入其他形态的标签,一般不进行修改 pos_label positive类别标签 average 多分类时指标计算方法 sample_weight 不同类别的样本权重 zero_division 当分母为0时返回结果
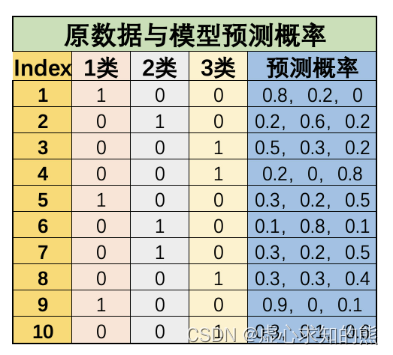
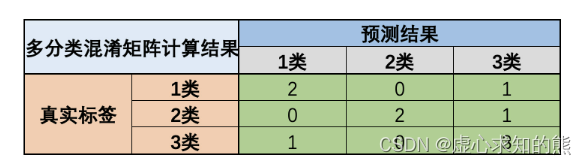
其中,需要重点介绍多分类问题时 average 参数不同取值时的计算方法。 此处以 recall 为例进行计算,重点介绍当 average 取值为 ‘macro’、‘micro’ 和 ‘weighted’ 的情况,其他指标也类似,例如有简单多分类问题如下:
我们令 1 类标签为 0、2 类标签为 1、3 类标签为 2,则上述数据集真实标签为: y_true = np. array( [ 0 , 1 , 2 , 2 , 0 , 1 , 1 , 2 , 0 , 2 ] )
y_pred = np. array( [ 0 , 1 , 0 , 2 , 2 , 1 , 2 , 2 , 0 , 2 ] )
tp1 = 2
tp2 = 2
tp3 = 3 fn1 = 1
fn2 = 1
fn3 = 1
接下来有两种计算 recall 的方法,其一是先计算每个类别的 recall,然后求均值: re1 = 2 / 3
re2 = 2 / 3
re3 = 3 / 4 np. mean( [ re1, re2, re3] )
这也就是 average 参数取值为 macro 时的计算结果: recall_score( y_true, y_pred, average= 'macro' )
当然,如果上述手动实现过程不求均值,而是根据每个类别的数量进行加权求和,则就是参数 average 参数取值为 weighted 时的结果: re1 * 3 / 10 + re2 * 3 / 10 + re3 * 4 / 10
recall_score( y_true, y_pred, average= 'weighted' )
当然,还有另外一种计算方法,那就是先计算整体的 TP 和 FN,然后根据整体 TP 和 FN 计算 recall: tp = tp1 + tp2 + tp3
fn = fn1 + fn2 + fn3tp / ( tp+ fn)
该过程也就是 average 参数取值 micro 时的计算结果: recall_score( y_true, y_pred, average= 'micro' )
对于上述三个不同参数的选取,首先如果是样本不平衡问题(如果是要侧重训练模型判别小类样本的能力的情况下)、则应排除 weighted 参数,以避免赋予大类样本更高的权重。 除此以外,在大多数情况下这三个不同的参数其实并不会对最后评估器的选取结果造成太大影响,只是在很多要求严谨的场合下需要说明多分类的评估结果的计算过程,此时需要简单标注下是按照何种方法进行的计算。 不过,如果是混淆矩阵中相关指标和 ROC-AUC 指标放在一起讨论,由于新版 sklearn 中 ROC-AUC 本身不支持在多分类时按照 micro 计算、只支持 macro 计算,因此建议混淆矩阵的多分类计算过程也选择 macro 过程,以保持一致。 不过值得注意的是,还有一种观点,尽管 micro 和 macro 方法在混淆矩阵相关指标的计算过程中差别不大,在 ROC-AUC 中,macro 指标并不利于非平衡样本的计算(混淆矩阵中可以通过 positive 的类别选择来解决这一问题),需要配合 OVR 分类方法才能够有所改善。 接下来继续讨论关于多分类的 ROC-AUC 评估指标的相关问题: from sklearn. metrics import roc_auc_score
能够发现,roc_auc_score 评估指标函数中大多数参数都和此前介绍的混淆矩阵中评估指标类似。 接下来我们简单尝试使用 ROC-AUC 函数进行评估指标计算,根据 ROC-AUC 的计算流程可知,此处我们需要在 y_pred 参数位中输入模型概率预测结果: y_true = np. array( [ 1 , 0 , 0 , 1 , 0 , 1 ] )
y_pred = np. array( [ 0.9 , 0.7 , 0.2 , 0.7 , 0.4 , 0.8 ] ) roc_auc_score( y_true, y_pred)
当然,如果我们在 y_pred 参数中输入分类结果,该函数也能计算出最终结果: y_true = np. array( [ 1 , 0 , 0 , 1 , 0 , 1 ] )
y_pred = np. array( [ 1 , 1 , 0 , 1 , 0 , 1 ] ) roc_auc_score( y_true, y_pred)
不过,此时模型会默认预测标签为 0 的概率结果为 0.4、预测标签为 1 的概率预测结果为 0.6,即上述结果等价于: y_true = np. array( [ 1 , 0 , 0 , 1 , 0 , 1 ] )
y_pred = np. array( [ 0.6 , 0.6 , 0.4 , 0.6 , 0.4 , 0.6 ] ) roc_auc_score( y_true, y_pred)
即计算过程会默认模型概率预测结果更差。 接下来详细解释 ROC-AUC 中其他参数: roc_auc_score?
Name Description max_fpr fpr最大值,fpr是roc曲线的横坐标 multi_class 分类器在进行多分类时进行的多分类问题处理策略
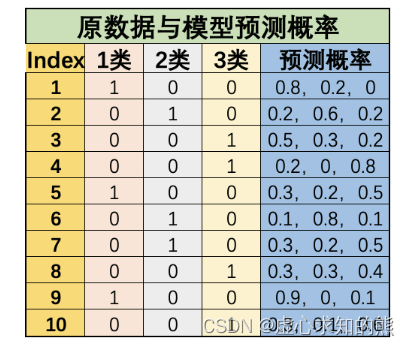
此处需要注意的是关于 multi_class 参数的选择。 一般来说 sklearn 中的 multi_class 参数都是二分类器中用于解决多元分类问题时的参数(如逻辑回归)。 由于 ROC-AUC 需要分类结果中的概率来完成最终计算,因此需要知道概率结果对应分类标签——即到底是以 OVO 还是 OVR 模式在进行多分类,因此如果是进行多分类 ROC-AUC 计算时,需要对其进行明确说明。 不过对于多分类逻辑回归来说,无论是 OVR 还是 MVM 策略,最终分类结果其实都可以看成是 OVR 分类结果,因此如果是多分类逻辑回归计算 ROC-AUC ,需要设置 multi_class 参数为 OVR 。 同时由于根据 ROC-AUC 的函数参数说明可知,在 multi_class 参数取为 OVR 时,average 参数取值为 macro 时能够保持一个较高的偏态样本敏感性,因此对于 ROC-AUC 来说,大多数时候 average 参数建议取值为 macro。 总结一下,对于 ROC-AUC 进行多分类问题评估时,建议选择的参数组合是 OVR/OVO+macro,而 OVR/OVO 的参数选择需要根据具体的多分类模型来定,如果是围绕逻辑回归多分类评估器来进行结果评估,则建议 ROC-AUC 和逻辑回归评估器的 multi_class 参数都选择 OVR。 在新版的 sklearn 中, ROC-AUC 函数的multi_class参数已不支持 micro 参数,面对多分类问题,该参数只能够在 macro 和 weighted 中进行选择。 接下来我们简单测算 average 参数中 macro 和 weighted 的计算过程。还是围绕上述数据集进行计算:
据此我们可以计算每个类别单独的 ROC-AUC 值: y_true_1 = np. array( [ 1 , 0 , 0 , 0 , 1 , 0 , 0 , 0 , 1 , 0 ] )
y_pred_1 = np. array( [ 0.8 , 0.2 , 0.5 , 0.2 , 0.3 , 0.1 , 0.3 , 0.3 , 0.9 , 0.3 ] ) r1 = roc_auc_score( y_true_1, y_pred_1)
r1
y_true_2 = np. array( [ 0 , 1 , 0 , 0 , 0 , 1 , 1 , 0 , 0 , 0 ] )
y_pred_2 = np. array( [ 0.2 , 0.6 , 0.3 , 0 , 0.2 , 0.8 , 0.2 , 0.3 , 0 , 0.1 ] ) r2 = roc_auc_score( y_true_2, y_pred_2)
r2
y_true_3 = np. array( [ 0 , 0 , 1 , 1 , 0 , 0 , 0 , 1 , 0 , 1 ] )
y_pred_3 = np. array( [ 0 , 0.2 , 0.2 , 0.8 , 0.5 , 0.1 , 0.5 , 0.4 , 0.1 , 0.6 ] ) r3 = roc_auc_score( y_true_3, y_pred_3)
r3
np. mean( [ r1, r2, r3] )
该结果应当和 macro+multi_class 参数计算结果相同 y_pred = np. concatenate( [ y_pred_1. reshape( - 1 , 1 ) , y_pred_2. reshape( - 1 , 1 ) , y_pred_3. reshape( - 1 , 1 ) ] , 1 )
y_pred
y_true = np. array( [ 0 , 1 , 2 , 2 , 0 , 1 , 1 , 2 , 0 , 2 ] ) roc_auc_score( y_true, y_pred, average= 'macro' , multi_class= 'ovr' )
当然,如果 ROC-AUC 函数的参数是 OVR+weighted,则计算结果过程验证如下: r1 * 3 / 10 + r2 * 3 / 10 + r3 * 4 / 10
roc_auc_score( y_true, y_pred, average= 'weighted' , multi_class= 'ovr' )
至此,我们就能够较为清楚的了解关于 F1-Score 和 ROC-AUC 评估指标在调用 sklearn 中相关函数解决多分类问题评估的具体方法。 在 Lesson 6.5 中我们已经完整总结了机器学习调参的基本理论,同时介绍了 sklearn 中网格搜索(GridSearchCV)评估器的参数及基本使用方法。 我们将进一步介绍网格搜索的进阶使用方法,并同时补充多分类问题评估指标在 sklearn 中实现的相关方法,然后围绕 Lesson 6.4 中提出的问题给出一个基于网格搜索的解决方案。 首先是关于评估器全参数的设置方法。 在此前的实验中,我们只是保守的选取了部分我们觉得会对模型产生比较大影响的超参数来构建参数空间,但在实际场景中,调参应该是纳入所有对模型结果有影响的参数进行搜索、并且是全流程中的参数来进行搜索。 也就是说我们设置参数的空间的思路不应该更加“激进”一些,首先是对逻辑回归评估器来说,应该是排除无用的参数外纳入所有参数进行调参,并且就逻辑回归模型来说,往往我们需要在模型训练前进行特征衍生以增强模型表现。 因此我们应该先构建一个包含多项式特征衍生的机器学习流、然后围绕这个机器学习流进行参数搜索,这才是一个更加完整的调参过程。 首先,仿造 Lesson 6.4 中展示过程创造数据集如下: np. random. seed( 24 )
X = np. random. normal( 0 , 1 , size= ( 1000 , 2 ) )
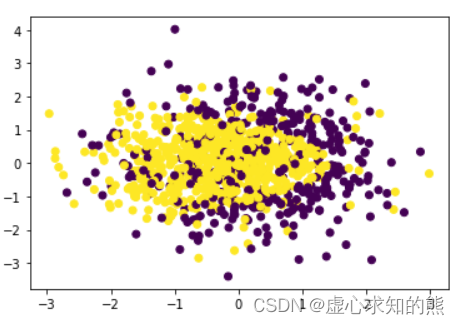
y = np. array( X[ : , 0 ] + X[ : , 1 ] ** 2 < 1.5 , int ) np. random. seed( 24 )
for i in range ( 200 ) : y[ np. random. randint( 1000 ) ] = 1 y[ np. random. randint( 1000 ) ] = 0 plt. scatter( X[ : , 0 ] , X[ : , 1 ] , c= y)
X_train, X_test, y_train, y_test = train_test_split( X, y, train_size= 0.7 , random_state = 42 )
pipe = make_pipeline( PolynomialFeatures( ) , StandardScaler( ) , LogisticRegression( max_iter= int ( 1e6 ) ) )
pipe. get_params( )
param_grid = [ { 'polynomialfeatures__degree' : np. arange( 2 , 10 ) . tolist( ) , 'logisticregression__penalty' : [ 'l1' ] , 'logisticregression__C' : np. arange( 0.1 , 2 , 0.1 ) . tolist( ) , 'logisticregression__solver' : [ 'saga' ] } , { 'polynomialfeatures__degree' : np. arange( 2 , 10 ) . tolist( ) , 'logisticregression__penalty' : [ 'l2' ] , 'logisticregression__C' : np. arange( 0.1 , 2 , 0.1 ) . tolist( ) , 'logisticregression__solver' : [ 'lbfgs' , 'newton-cg' , 'sag' , 'saga' ] } , { 'polynomialfeatures__degree' : np. arange( 2 , 10 ) . tolist( ) , 'logisticregression__penalty' : [ 'elasticnet' ] , 'logisticregression__C' : np. arange( 0.1 , 2 , 0.1 ) . tolist( ) , 'logisticregression__l1_ratio' : np. arange( 0.1 , 1 , 0.1 ) . tolist( ) , 'logisticregression__solver' : [ 'saga' ] }
]
根据此前介绍,如果需要更好的验证模型本身泛化能力,建议使用 F1-Score 或者 ROC-AUC,当然调整网格搜索过程的模型评估指标过程其实并不难理解,核心就是修改 scoring 参数取值。 但由于涉及到在参数中调用评估函数,因此需要补充一些关于常用分类评估指标在 sklearn 中的函数使用方法,以及不同评估指标函数在不同参数取值时在网格搜索评估器中的调用方法。 GridSearchCV?
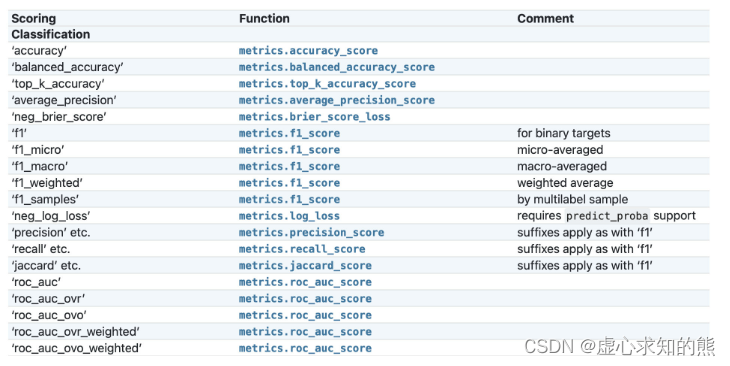
从评估器的说明文档中能够看出,scoring 参数最基础的情况下可以选择输入 str(字符串)或者 callable(可调用)对象,也就是可以输入指代某个评估过程的字符串(一个字符串代表不同参数取值下的某评估函数),或者直接输入某评估指标函数(或者通过 make_score 函数创建的函数),来进行模型结果的评估。 当然,也可以在该参数位上直接输入一个字典或者 list,其中,如果是字典的话字典的 value 需要是 str(字符串)或者 callable(可调用)对象。 由于 sklearn 中的评估指标函数一般都是有多个不同参数,而不同参数代表不同的计算过程,因此这些评估指标函数作为参数输入网格搜索评估器中的时候,必须通过“某种方式”确定这些参数取值. 因此就有了如下方法,即通过字符串对应表来查看不同字符串所代表的不同参数取值下的评估指标函数,如下所示:
不难看出,在网格搜索中输出评估指标参数,和调用评估指标函数进行数据处理还是有很大的区别。 例如,metrics.roc_auc_score 函数能够同时处理多分类问题和二分类问题,但如果作为参数输入到网格搜索中,roc_auc 参数只能指代 metrics.roc_auc_score 函数的二分类功能. 如果需要进行多分类,则需要在 scoring 参数中输入 roc_auc_ovr、roc_auc_ovo 或者 roc_auc_ovr_weighted、roc_auc_ovo_weighted。 我们先简单尝试在 scoring 中输入字符串的基本操作,然后在深入解释 ROC-AUC 评估指标的使用方法。 同时,该参数列表也可以通过如下方式获得: import sklearn
sorted ( sklearn. metrics. SCORERS. keys( ) ) from sklearn. metrics import roc_auc_scoreroc_auc_score?
例如字符串 roc_auc_ovr 就代表 roc_auc_score 函数中 multi_class 参数取值为 ovr 时的计算流程。 也就是说,当网格搜索的 scoring 参数取值为字符串 roc_auc_ovr 时,就代表调用了 multi_class=`ovr`、而其他参数选用默认参数的 roc_auc_score 函数作为模型评估函数。 GridSearchCV( estimator= pipe, param_grid= param_grid, scoring= 'roc_auc_ovr' )
当然,scoring 参数还支持直接输入可调用对象,即支持输入经过 make_scorer 函数转化之后的评估指标函数: from sklearn. metrics import make_scoreracc = make_scorer( roc_auc_score) GridSearchCV( estimator= pipe, param_grid= param_grid, scoring= acc)
但此时我们无法修改评估指标函数的默认参数。 值得注意的是,此处 make_scorer 函数实际上会将一个简单的评估指标函数转化为评估器结果评估函数。 对于评估指标函数来说,只需要输入标签的预测值和真实值即可进行计算,例如: accuracy_score( [ 1 , 1 , 0 ] , [ 1 , 1 , 1 ] )
而评估器结果评估函数,则需要同时输入评估器、特征矩阵以及对应的真实标签,其执行过程是先将特征矩阵输入评估器、然后将输出结果和真实标签进行对比: acc = make_scorer( accuracy_score) acc( search. best_estimator_, X_train, y_train)
search. score( X_train, y_train)
而在网格搜索或者交叉验证评估器中,只支持输入经过 make_scorer 转化后的评估指标函数。 当然,有的时候我们可能需要同时看不同参数下多项评估指标的结果,此时我们就可以在 scoring 中输入列表、元组或者字典,当然字典对象会较为常用。 例如如果我们需要同时选用 roc-auc 和 accuracy 作为模型评估指标,则需要创建如下字典: scoring = { 'AUC' : 'roc_auc' , 'Accuracy' : make_scorer( accuracy_score) }
GridSearchCV?search = GridSearchCV( estimator= clf, param_grid= param_grid_simple, scoring= scoring, refit= 'Accuracy' )
当然,roc-auc 指标也可以用 make_score 来传输,accuracy 也可以用字符串形式来传输,即来上述多评估指标的字典等价于: { 'AUC' : make_scorer( roc_auc_score) , 'Accuracy' : 'accuracy' }
不过,需要注意的是,尽管此时网格搜索评估器将同时计算一组参数下的多个评估指标结果并输出,但我们只能选取其中一个评估指标作为挑选超参数的依据,而其他指标尽管仍然会计算,但结果只作参考。 而 refit 参数中输入的评估指标,就是最终选择参数的评估指标 尽管网格搜索支持依据不同的评估指标进行参数搜索,但最终选择何种参数,可以参考如下依据: 有明确模型评估指标的 在很多竞赛或者项目算法验收环节,可能都会存在较为明确的模型评估指标,例如模型排名根据 f1-score 计算结果得出等。在该情况下,应当尽量选择要求的评估指标。 没有明确模型评估指标的 但是,如果没有明确的评估指标要求,则选择评估指标最核心的依据就是尽可能提升/确保模型的泛化能力。 此时,根据 Lesson 5 中对各评估指标的讨论结果,如果数据集的各类别并没有明确的差异,在算力允许的情况下,应当优先考虑 roc-auc。 而如果希望重点提升模型对类别 1(或者某类别)的识别能力,则可以优先考虑 f1-score 作为模型评估指标。 接下来,依据上述优化后的过程,来执行网格搜索。完整流程如下: (1) 构造机器学习流
pipe = make_pipeline( PolynomialFeatures( ) , StandardScaler( ) , LogisticRegression( max_iter= int ( 1e6 ) ) )
param_grid = [ { 'polynomialfeatures__degree' : np. arange( 2 , 10 ) . tolist( ) , 'logisticregression__penalty' : [ 'l1' ] , 'logisticregression__C' : np. arange( 0.1 , 2 , 0.1 ) . tolist( ) , 'logisticregression__solver' : [ 'saga' ] } , { 'polynomialfeatures__degree' : np. arange( 2 , 10 ) . tolist( ) , 'logisticregression__penalty' : [ 'l2' ] , 'logisticregression__C' : np. arange( 0.1 , 2 , 0.1 ) . tolist( ) , 'logisticregression__solver' : [ 'lbfgs' , 'newton-cg' , 'sag' , 'saga' ] } , { 'polynomialfeatures__degree' : np. arange( 2 , 10 ) . tolist( ) , 'logisticregression__penalty' : [ 'elasticnet' ] , 'logisticregression__C' : np. arange( 0.1 , 2 , 0.1 ) . tolist( ) , 'logisticregression__l1_ratio' : np. arange( 0.1 , 1 , 0.1 ) . tolist( ) , 'logisticregression__solver' : [ 'saga' ] }
]
(3) 实例化网格搜索评估器 考虑到实际参数空间较大,网格搜索需要耗费较长时间,此处使用单一指标 roc 作为参数选取指标进行搜索: search = GridSearchCV( estimator= pipe, param_grid= param_grid, scoring= 'roc_auc' , n_jobs= 5 )
search. fit( X_train, y_train)
search. best_score_
search. best_params_
需要注意的是,上述 best_score_ 属性查看的结果是在 roc-auc 评估指标下,默认五折交叉验证时验证集上的 roc-auc 的平均值。 但如果我们对训练好的评估器使用 .socre 方法,查看的仍然是 pipe 评估器默认的结果评估方式,也就是准确率计算结果: search. best_estimator_. score( X_train, y_train)
search. best_estimator_. score( X_test, y_test)
accuracy_score( search. best_estimator_. predict( X_train) , y_train)
accuracy_score( search. best_estimator_. predict( X_test) , y_test)
(6) 结果分析 最终模型结果准确率在 78% 上下。当然,如果只看模型准确率结果,我们发现该结果相比 Lesson 6.4 中结果较差(Lesson 6.4 中测试集最高得分达到 0.8)。 但是,该模型相比 Lesson 6.4 中模型来看,该模型基本没有过拟合隐患(测试集分数甚至高于训练集),因此该模型在未来的使用过程中更有可能能够确保一个稳定的预测输出结果(泛化能力更强)。这也是交叉验证和 roc-auc 共同作用的结果。 当然,如果有明确要求根据准确率判断模型效果,则上述过程应该选择准确率,同时如果算力允许,也可以近一步扩大搜索空间(Lesson 6.4 中 0.8 的准确率就是在 15 阶多项式特征衍生基础上进行的运算)。 至此,我们就完成了在实验数据上的建模调优。