视觉SLAM十四讲：从理论到实践（Chapter7：视觉里程计1）
前言
学习笔记，仅供学习，不做商用，如有侵权，联系我删除即可
一、目标
1.理解图像特征点的意义，并掌握在单幅图像中提取特征点及多幅图像中匹配特征点的方法。
2.理解对极几何的原理，利用对极几何的约束，恢复图像之间的摄像机的三维运动。
3.理解PNP问题，以及利用已知三维结构与图像的对应关系求解摄像机的三维运动。
4.理解ICP问题，以及利用点云的匹配关系求解摄像机的三维运动。
5.理解如何通过三角化获得二维图像上对应点的三维结构。
二、特征点法
视觉里程（Visual Odometry）：计算前后两帧位姿的变化量
VO主要有两个大类：特征点法和直接法。
特征点法最大的一个案例就是ORB-SLAM。
2.1 特征点
特征点由关键点(Key-point)和描述子(Descriptor)组成。
2.2 ORB特征
ORB(Oriented FAST and Rotated BRIEF)
关键点：FAST角点
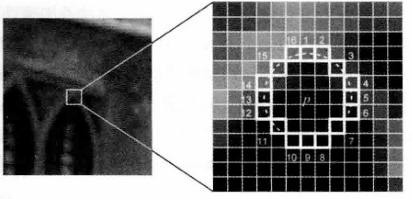
描述子：BRIEF（一种二进制描述子，速度非常快）
2.3 特征匹配
Hamming distance：两个二进制串之间的比较，相同为1，不同为0.
暴力匹配(Brute-Force Matcher)：A中的每个特征点依次和B中所有的特征点比较距离，取最近的一个作为匹配点。
加速方法：快速最近邻（FLANN）
2.4 计算相机运动
三、2D-2D：对极几何
对极几何是研究两幅图像之间存在的关系的几何。它与场景结构无关，只依赖于相机的内外参数，可广泛用于图像匹配、三维重建方面。
3.1 对极约束
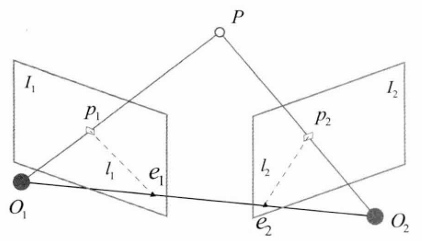
空间点P的世界坐标：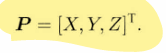
像素点p1，p2的像素坐标：
，其中：K：内参矩阵，R,t：外参矩阵，s1p1和p1是投影关系，在齐次坐标上是相等的（尺度意义下相等）。
把s除过取，再使用归一化坐标：
基础矩阵F（和内参和外参都有关）和本质矩阵E （只和外参有关，内参已知的情况下）
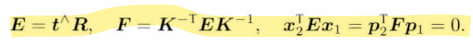
3.2 本质矩阵
最后可以得到如下方程：
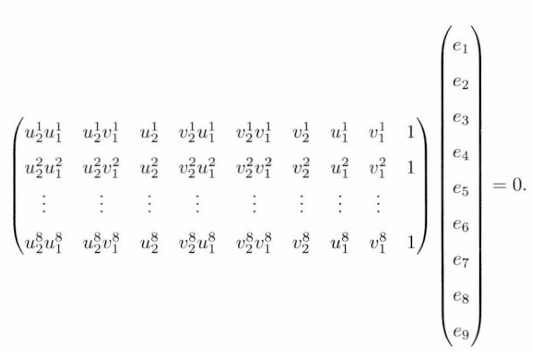
Ax=0可以用SVD方法计算出x的值。
从E中分离出R和t的方法是：
，该方法会有4个可能的解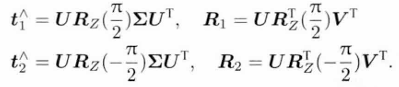
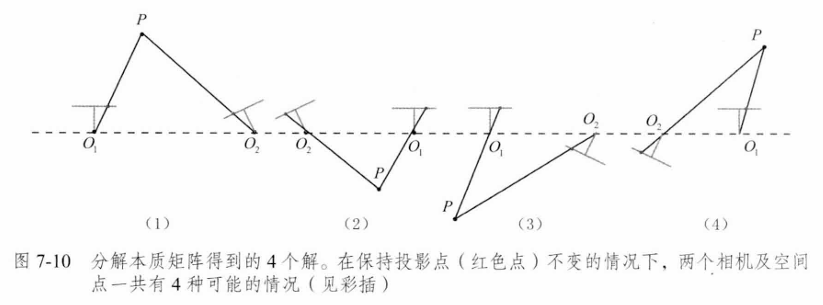
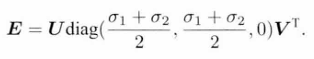
八点法用于初始换，但有尺度不确定性，而且不能用于纯旋转问题，多于八个点会用最小二乘法或RANSAC算法。
3.3 单应矩阵
平面方程：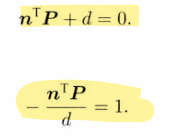
于是有：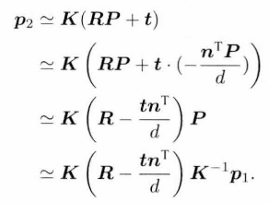
把中间部分记作H，则有：
H即为单应矩阵。
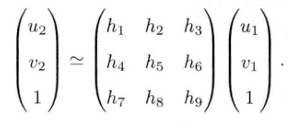
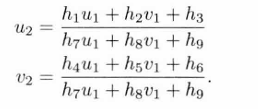整理得：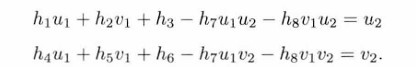
强制令h9=1，可得：
类似于Ax=b的方程，可用SVD分解或者最小二乘法优化算法求解。
四、三角测量
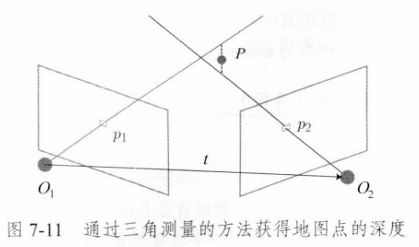
R,t已经求解出结果，只有深度未知，求解深度即可
但三角测量的误差与基线长度有关：
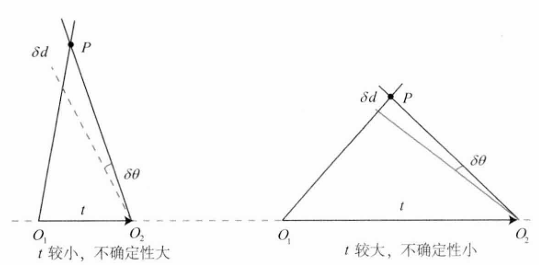
相机初始化：
特征点提取 --> 特征匹配 --> 求解E或F --> 根据E或F分解出R,t --> 三角化恢复三维坐标
五、3D-2D：PnP
真实点3D坐标和像素点的2D坐标已知，相机可以通过标定得到内参，进而计算相机位姿R,t的算法。
P3P，DLT，EPnP，UPnP等算法，PnP只是求解出一个初值，后面还需要用光束平差法（Bundle Adjustment, BA）进行优化。
5.1 DLT（直接线性变换）
一个点对可以提供两个方程，DLT有12个未知数，所以至少6个点对就可以求解。
现在最常用的是EPnP