算法入门----小话算法(1)
下面就首先从一些数学问题入手。
Q1: 如何证明时间复杂度O(logN) < O(N) < O(NlogN) < O(N2) < O(2N) < O(N!) < O(NN)?
A: 如果一个以整数为参数的不等式不能很容易看出不等的关系,那么最好用图示或者数学归纳法。
很显然,使用图示的方法也不能很好得到上面的关系图,因为图示范围较小,不能证明当N趋于无穷大依然成立。所以,数学归纳法成为首选。
不失一般性,假设logN的底数为2:
欲证明O(logN) < O(N),只需要证明log2N < N = log22N, 只需要证明N < 2N
当N = 1时成立,假设上面成立,现在只要证明N + 1 < 2N+1
这个显然成立。
O(N) < O(NlogN) 很容易证明,这里不再证明;
由O(logN) < O(N), 很容易证明 O(NlogN) < O(N2)
对于O(N2) < O(2N) < O(N!) < O(NN),由上面的方法同样很容易证明,这里不再赘述。
Q2:如何证明1+2+.....+n = n(n+1)/2 ?
A: 对于以整数n为变量的表达式的证明方式当然是数学归纳法。
当n=1时,很显然成立;假设等于n的时候也成立,下面就要证明当等于n+1的时候依然成立。
1+2+...+n+(n+1) = n(n+1)/2+(n+1)=(n+1)(n+2)/2.显然成立。所以证明此等式成立。
当然,证明这个还可以用高斯的NB计算方法:
假设S=1+2+...+(n-1)+n
同样S=n+(n-1)+...+2+1
所以两式相加: 2S=(n+1)+(n+1)+...+(n+1)+(n+1)=n(n+1);
所以S=n(n+1)/2.
当然,还有另外一种画图的方式来证明:
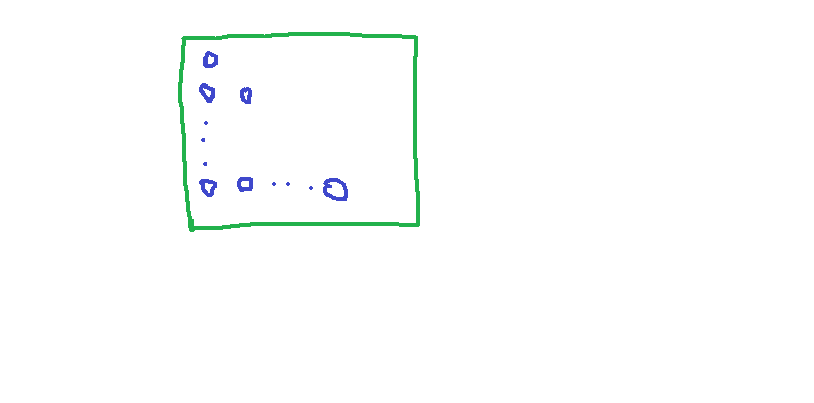
如上图,在一个边长为n的正方形里面,存放了1,2,...n这些小圆圈。
可以看出,(1+2+...+n)*2=n*n+n;
所以1+2+...+n=n(n+1)/2.
微风不燥,阳光正好,你就像风一样经过这里,愿你停留的片刻温暖舒心。
我是程序员小迷(致力于C、C++、Java、Kotlin、Android、Shell、JavaScript、TypeScript、Python等编程技术的技巧经验分享),若作品对您有帮助,请关注、分享、点赞、收藏、在看、喜欢,您的支持是我们为您提供帮助的最大动力。
欢迎关注。助您在编程路上越走越好!
