当前位置：首页 > news >正文

day15|各种遍历的应用

news 2025/7/26 9:39:59

相关题目：
层次遍历会一打十
反转二叉树
对称二叉树

层次遍历会一打十

自底向上的层序遍历

在这里插入图片描述
实现思路：层次遍历二叉树，将遍历后的结果revers即可

public List<List<Integer>> levelOrderBottom(TreeNode root) {List<List<Integer>> res = new ArrayList<>();Queue<TreeNode> que = new ArrayDeque<>();if (root == null) {return res;}que.offer(root);int size = 0;while (!que.isEmpty()) {size = que.size();List<Integer> list = new ArrayList<>();while (size > 0) {TreeNode cur = que.poll();list.add(cur.val);if (cur.left != null) {que.offer(cur.left);}if (cur.right != null) {que.offer(cur.right);}size--;}res.add(list);}Collections.reverse(res);return res;}

输出二叉树的右视图节点

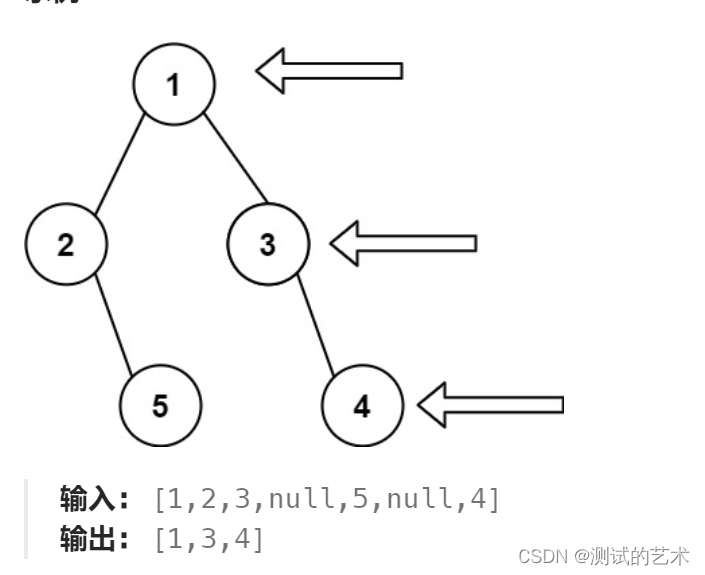
在这里插入图片描述
实现思路：层次遍历二叉树，记录二叉树每一层的节点数，到达该层最后一个节点时，将其加入到结果集即可

public List<Integer> rightSideView(TreeNode root) {List<Integer> res = new ArrayList<>();if(root == null){return res;}Queue<TreeNode> que = new ArrayDeque<>();que.offer(root);int size = 0;while(!que.isEmpty()){size = que.size();while(size>0){TreeNode cur = que.poll();//遍历到该层最后一个节点if(size == 1){res.add(cur.val);}if(cur.left!=null){que.offer(cur.left);}if(cur.right!=null){que.offer(cur.right);}size--;}}return res;}

二叉树每层的平均值

在这里插入图片描述
实现思路：层次遍历二叉树，计算每一层的平均值，注意：每层数之和及平均值的数据类型

public List<Double> averageOfLevels(TreeNode root) {List<Double> res = new ArrayList<>();Queue<TreeNode> que = new ArrayDeque<>();if(root == null){return res;}int size = 0;que.offer(root);while(!que.isEmpty()){size = que.size();double sum = 0;for (int i = 0; i < size; i++) {TreeNode cur = que.poll();sum += cur.val;if(cur.left!=null){que.offer(cur.left);}if(cur.right!=null){que.offer(cur.right);}}res.add(sum/size);}return res;}

N叉树的·层次遍历

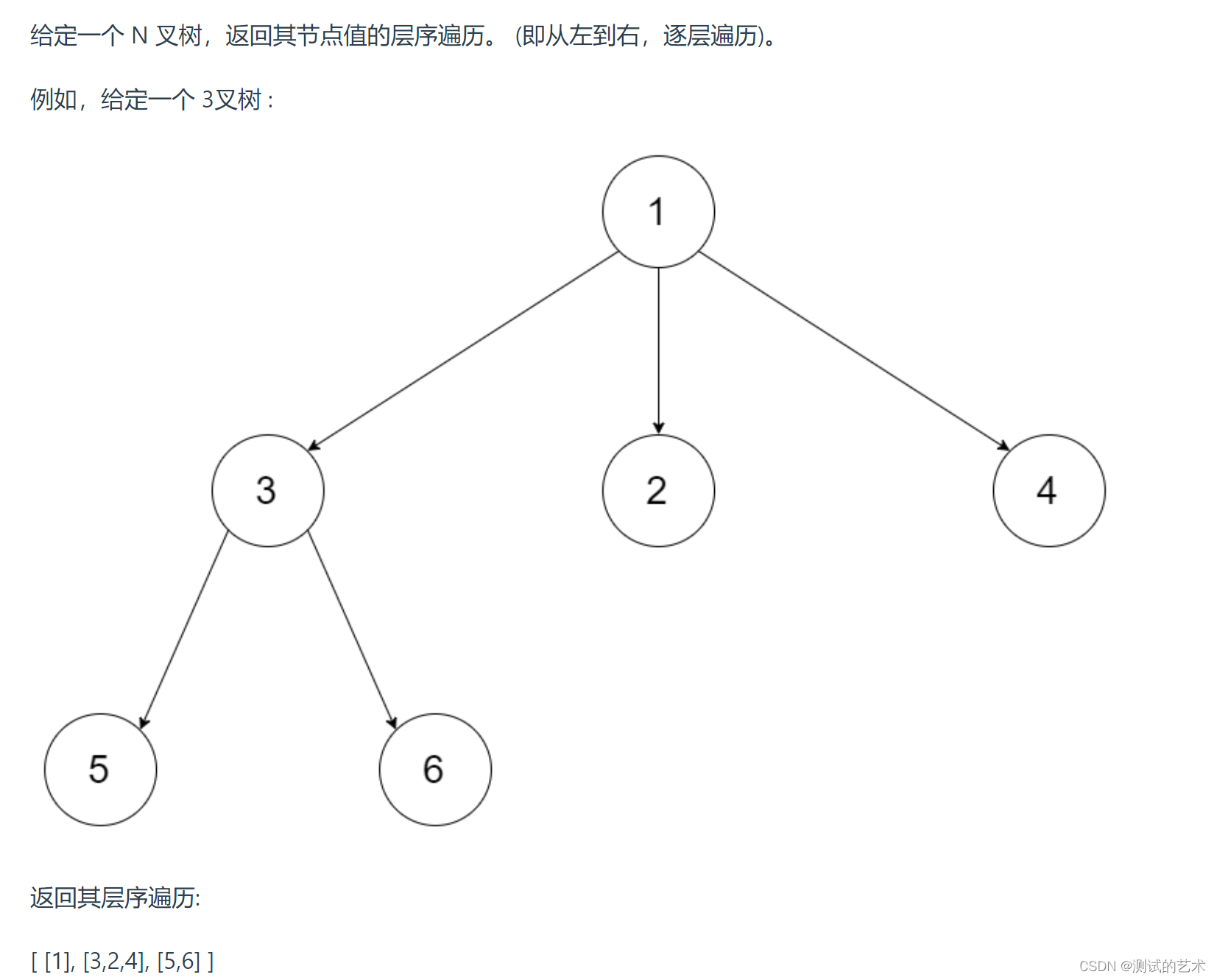
在这里插入图片描述

class Node {public int val;public List<Node> children;public Node() {}public Node(int _val) {val = _val;}public Node(int _val, List<Node> _children) {val = _val;children = _children;}
};public class LevelOrderNode {public List<List<Integer>> levelOrder(Node root) {List<List<Integer>> res = new ArrayList<>();if (root == null) {return res;}Queue<Node> que = new ArrayDeque<>();que.offer(root);while (!que.isEmpty()) {int size = que.size();List<Integer> list = new ArrayList<>();for (int i = 0; i < size; i++) {Node cur = que.poll();list.add(cur.val);List<Node> children = cur.children;if (children == null || children.size() == 0) {continue;}for (Node child : children) {if (child != null) {que.offer(child);}}}res.add(list);}return res;}}

在二叉树的每一行中找最大值

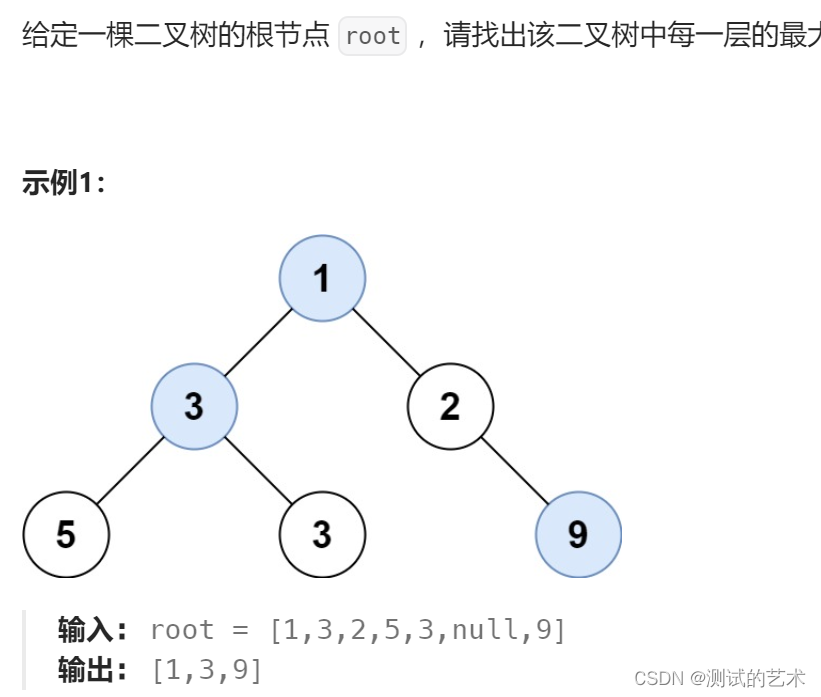
在这里插入图片描述
实现思路：层次遍历二叉树，记录每一层的最大值

public List<Integer> largestValues(TreeNode root) {List<Integer> res = new ArrayList<>();if(root == null){return res;}Queue<TreeNode> que = new ArrayDeque<>();int size = 0;que.offer(root);while(!que.isEmpty()){size = que.size();int max = Integer.MIN_VALUE;while(size>0) {TreeNode cur = que.poll();max = Math.max(max,cur.val);if(cur.left!=null){que.offer(cur.left);}if(cur.right!=null){que.offer(cur.right);}size--;}res.add(max);}return res;}

填充每个节点的下一个右侧节点指针

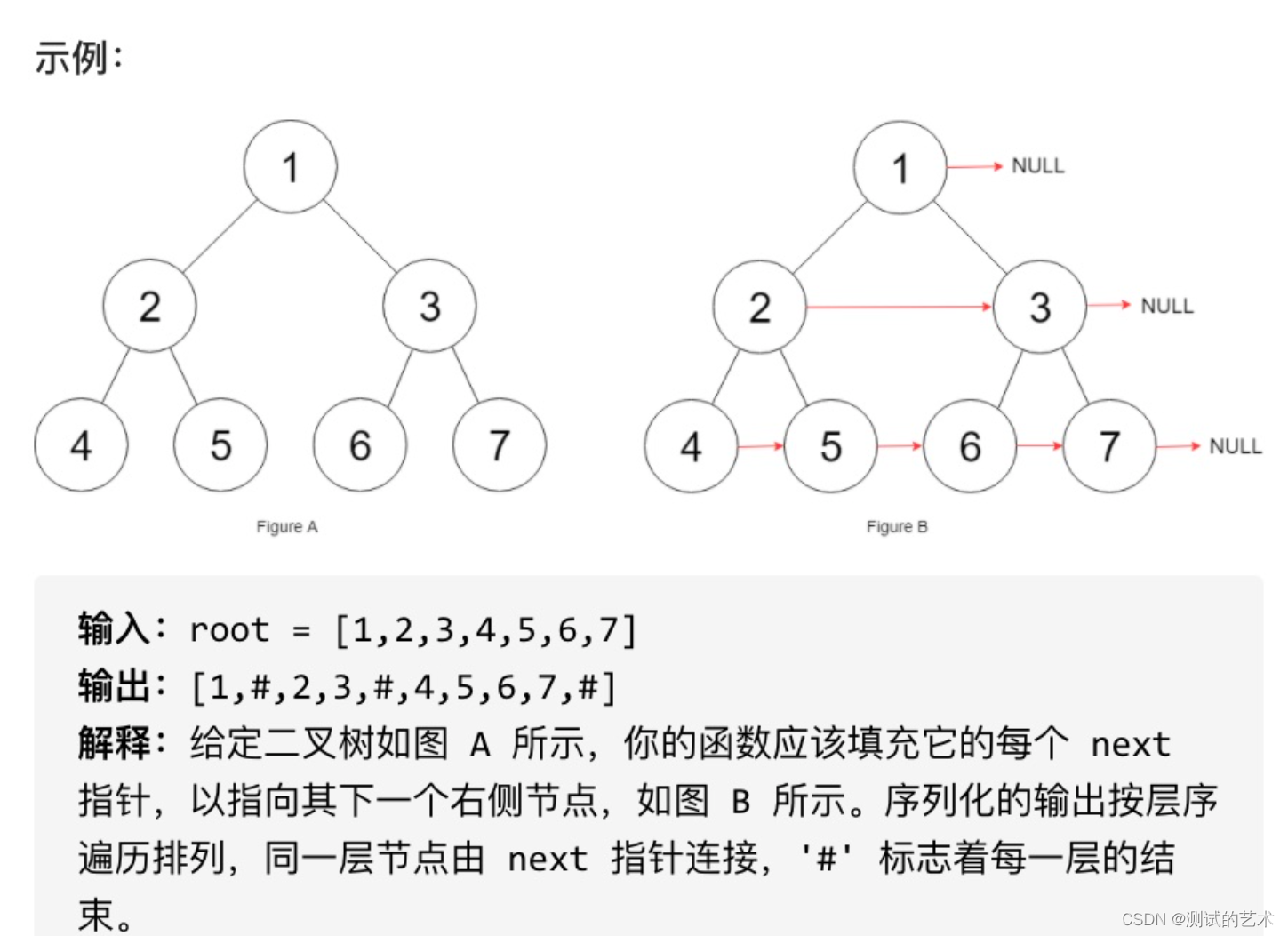
在这里插入图片描述
实现思路：层次遍历二叉树，记录每层元素个数，遍历每层元素，元素个数大于1时，使其next指针指向队头元素；元素个数为1时，使其next指针指向null即可

class NodeText {public int val;public NodeText left;public NodeText right;public NodeText next;public NodeText() {}public NodeText(int _val) {val = _val;}public NodeText(int _val, NodeText _left, NodeText _right, NodeText _next) {val = _val;left = _left;right = _right;next = _next;}
};
public class Connect {public NodeText connect(NodeText root) {Queue<NodeText> que = new ArrayDeque<>();if(root == null){return root;}que.offer(root);while(!que.isEmpty()){int size = que.size();while(size>0){NodeText cur = que.poll();if(size>1){NodeText temp = que.peek();cur.next = temp;}else{cur.next =null;}if(cur.left!=null){que.offer(cur.left);}if(cur.right!=null){que.offer(cur.right);}size--;}}return root;}
}

求二叉树的最大深度

在这里插入图片描述
实现思路：层次遍历二叉树，记录树的层数

public int maxDepth(TreeNode root) {int maxDepth = 0;int size = 0;if(root == null){return 0;}Queue<TreeNode> que = new ArrayDeque<>();que.offer(root);while(!que.isEmpty()){maxDepth++;size = que.size();while(size>0){TreeNode cur = que.poll();if(cur.left!=null){que.offer(cur.left);}if(cur.right!=null){que.offer(cur.right);}size--;}}return maxDepth;}

求二叉树的最小深度

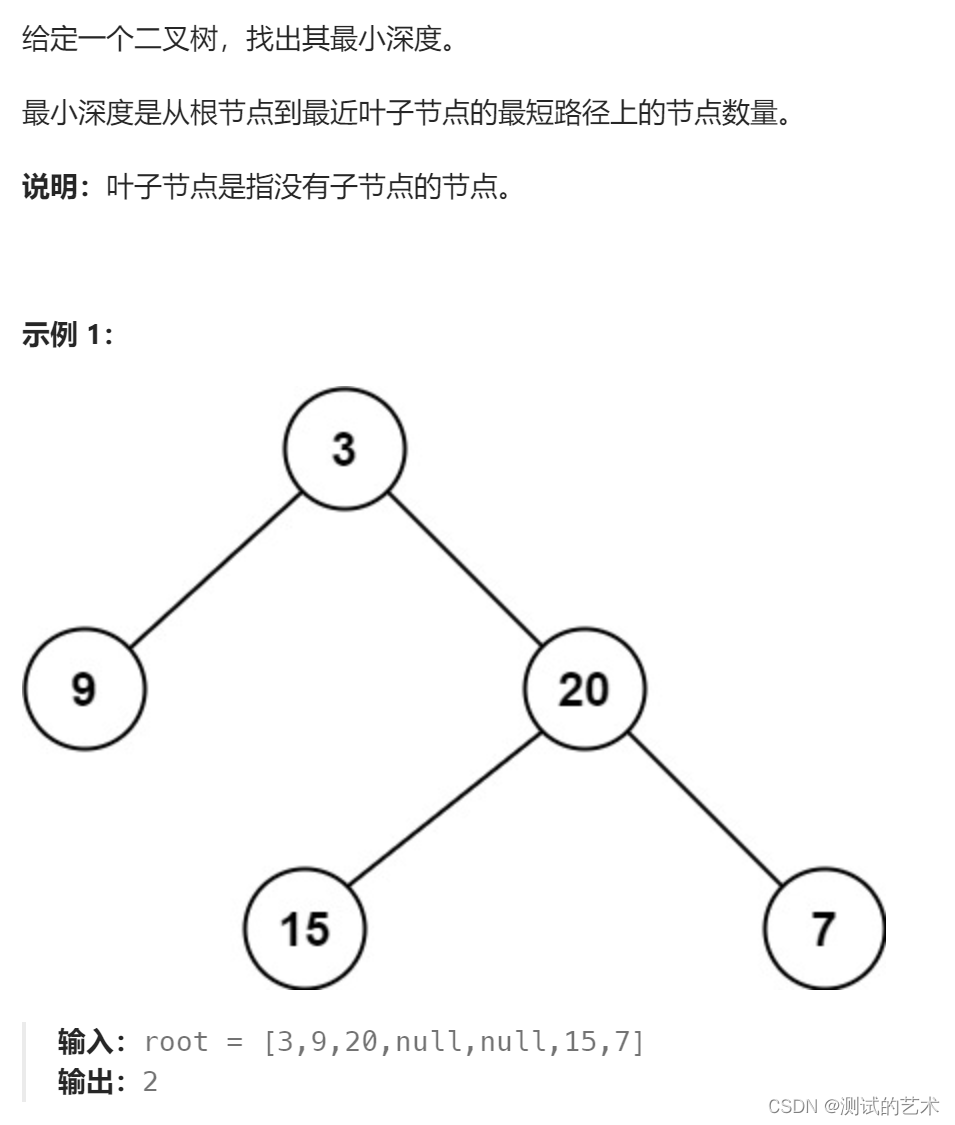
在这里插入图片描述

实现思路：层次遍历二叉树，当某个节点的左右孩子均为null时，输出该节点所在层数，及就是树的最小深度

public int minDepth(TreeNode root) {if (root == null) {return 0;}int deep = 0;int size = 0;Queue<TreeNode> que = new ArrayDeque<>();que.offer(root);while (!que.isEmpty()) {deep++;size = que.size();while (size > 0) {TreeNode cur = que.poll();if (cur.left == null && cur.right == null) {return deep;} else {if (cur.left != null) {que.offer(cur.left);}if (cur.right != null) {que.offer(cur.right);}}size--;}}return deep;}

反转二叉树（掌握递归遍历）

实现方法：使用前序遍历、后序遍历及其层次遍历均可实现
前序遍历实现方法：遍历中间节点，中间节点的左右孩子交换位置即可
后序遍历实现方法：遍历的左子树和右子树，交换中间节点左右孩子交换位置即可
层次遍历：遍历每一层的各个节点，反转各个节点的左右孩子即可

public class InvertTree extends TreeNode {public TreeNode invertTree(TreeNode root) {if(root == null){return null;}
//        //前序
//        swap(root);
//        invertTree(root.left);
//        invertTree(root.right);//        //后序
//        invertTree(root.left);
//        invertTree(root.right);
//        swap(root);//层次遍历--迭代Queue<TreeNode> que = new ArrayDeque<>();int size = 0;que.offer(root);while(!que.isEmpty()){size = que.size();while(size>0){TreeNode cur = que.poll();swap(cur);if(cur.left!=null){que.offer(cur.left);}if(cur.right!=null){que.offer(cur.right);}size--;}}return root;}public void swap(TreeNode root){TreeNode temp = root.left;root.left = root.right;root.right = temp;}
}

对称二叉树

递归实现：
递归三部曲

确定递归函数的参数和返回值
因为我们要比较的是根节点的两个子树是否是相互翻转的，进而判断这个树是不是对称树，所以要比较的是两个树，参数自然也是左子树节点和右子树节点。
返回值自然是bool类型。
代码如下：
bool compare(TreeNode* left, TreeNode* right)
确定终止条件
要比较两个节点数值相不相同，首先要把两个节点为空的情况弄清楚！否则后面比较数值的时候就会操作空指针了。
节点为空的情况有：（注意我们比较的其实不是左孩子和右孩子，所以如下我称之为左节点右节点）

左节点为空，右节点不为空，不对称，return false
左不为空，右为空，不对称 return false
左右都为空，对称，返回true
左右都不为空，比较节点数值，不相同就return false
代码如下：

if (left == NULL && right != NULL) return false;
else if (left != NULL && right == NULL) return false;
else if (left == NULL && right == NULL) return true;
else if (left->val != right->val) return false; // 注意这里我没有使用else

注意上面最后一种情况，我没有使用else，而是else if，因为我们把以上情况都排除之后，剩下的就是左右节点都不为空，且数值相同的情况。
3. 确定单层递归的逻辑
此时才进入单层递归的逻辑，单层递归的逻辑就是处理左右节点都不为空，且数值相同的情况。

比较二叉树外侧是否对称：传入的是左节点的左孩子，右节点的右孩子。
比较内侧是否对称：传入左节点的右孩子，右节点的左孩子。

如果左右都对称就返回true ，有一侧不对称就返回false 。
实现过程：

class Solution {public boolean isSymmetric(TreeNode root) {if (root == null) {return true;}return compare(root.left,root.right);}//递归实现public boolean compare(TreeNode left, TreeNode right) {if (left == null && right != null) return false;else if (left != null && right == null) return false;else if (left != null && right != null && left.val != right.val) return false;else if (left == null && right == null) return true;boolean inside = compare(left.left, right.right);boolean outside = compare(left.right, right.left);return inside && outside;}
}

查看全文

http://www.lryc.cn/news/351852.html