回溯法——(2)n皇后问题(C语言讲解)(LeetCode51 N皇后思想)(4皇后棋盘画图举例)(附代码)
目录
一、问题概括
二、算法分析
三、举例(4皇后棋盘)
四、算法实现
4.1运行结果:
51. N 皇后 - 力扣(LeetCode)
一、问题概括
n皇后问题是19世纪著名数学家高斯于1850年提出的。
问题是:在n×n的棋盘上摆放n个皇后,使其不能相互攻击,即任意两个皇后都不能处于同一行、同一列或同一斜线上。
二、算法分析
按照国际象棋规则,皇后可以攻击与之在同一行或同一列或同一斜线上的棋子。
核心分析:
n后问题等价于在n×n格的棋盘上放置n个皇后,任何2个皇后不放在同一行或同一列或同一斜线上。
由以上问题与分析可知,棋盘每一行可以并且必须拜访1个皇后。
1、那么n皇后问题的可能解用1个n元向量(x1,x2,......,xn)表示,即第i个皇后摆放在第i行第xi列的位置(1≤i≤n且1≤xi≤n)。
2、由于两个皇后不能位于同一列,所以,n皇后问题的解的向量必须满足约束条件xi≠xj。
3、不在同一斜线上的约束条件|i-j|≠|xi-xj|。
三、举例(4皇后棋盘)
下面将利用4皇后问题详细讲解。
(Q代表皇后放置符号,×代表放置失败的符号)
①首先把皇后1摆放到所在第一行第一列。

②皇后2本着不能与皇后1同行同列同斜线的原则 ,经过不懈努力尝试最终放置在了第二行第三列。

③皇后3根据同样的原理(同行同列同斜线的原则)尝试了第三行的任何一列都冲突。

④因此进行回溯,将皇后2摆放到下一个位置, 即皇后2第二行第四列。
⑤皇后3再次本着同行同列同斜线的原则,摆放到第三行第二列。

⑥
1、皇后4,摆放到第四行任何一列,都会违背同行同列同斜线的原则,进行回溯;
2、发现皇后3除了摆放到第三行第二列不违背原则,其他列放置同样违背原则,因此我们继续回溯;
3、但当我们此时回溯到皇后2时发现皇后2已经位于相应行最后一列了,所以我们只能继续回溯;
4、回溯到皇后1,将皇后1摆放到第一行第二列。

⑦接下来,将皇后2摆放到第二行第四列,皇后3摆放到第三行第一列,皇后4摆放到第四行第三列的位置,便得到了4皇后问题的一个解。

四、算法实现
#include <stdio.h>
#include <stdlib.h>#define N 4 // 可以更改 N 的值来解决不同大小的皇后问题
int count = 0;void printBoard(int board[N][N]);// 函数来检查是否可以在 board[row][col] 放置皇后
int isSafe(int board[N][N], int row, int col) {int i, j;// 检查同一列for (i = 0; i < row; i++)if (board[i][col] == 1)return 0;// 检查左上对角线for (i = row, j = col; i >= 0 && j >= 0; i--, j--)if (board[i][j] == 1)return 0;// 检查右上对角线for (i = row, j = col; i >= 0 && j < N; i--, j++)if (board[i][j] == 1)return 0;return 1;
}// 函数来解决 N 皇后问题
void solveNQUtil(int board[N][N], int row, int& solutions) {// 如果所有皇后都放置完成if (row >= N) {solutions++;printBoard(board);return;}// 在当前行尝试放置皇后并递归地放置剩下的皇后for (int col = 0; col < N; col++) {// 检查放置皇后的位置是否安全if (isSafe(board, row, col)) {board[row][col] = 1; // 放置皇后solveNQUtil(board, row + 1, solutions); // 递归放置下一个皇后board[row][col] = 0; // 回溯}}
}// 打印棋盘函数
void printBoard(int board[N][N]) {printf("Solution %d:\n", ++count);for (int i = 0; i < N; i++) {for (int j = 0; j < N; j++)printf("%d ", board[i][j]);printf("\n");}printf("\n");
}// 用于解决 N 皇后问题的主函数
void solveNQ() {int board[N][N] = { 0 }; // 初始化棋盘int solutions = 0;solveNQUtil(board, 0, solutions);printf("Total number of solutions are %d\n", solutions);
}// 主函数
int main() {solveNQ();return 0;
}4.1运行结果:
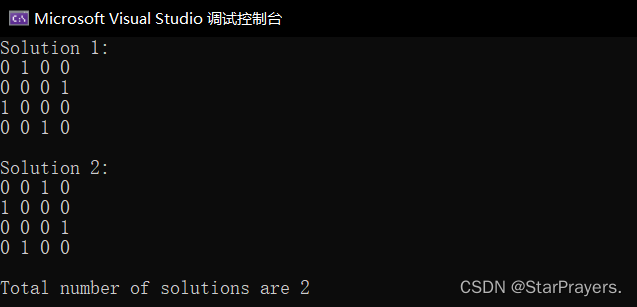
这个代码尝试在棋盘的每一行放置皇后,并使用递归来检查每个位置是否安全。如果找到一个安全的放置位置,就会递归地尝试下一行。这个过程一直重复,直到所有皇后都被放置在棋盘上。每次成功放置所有皇后时,它都会增加解决方案的数量,并打印出当前棋盘作为一个新的解决方案。
