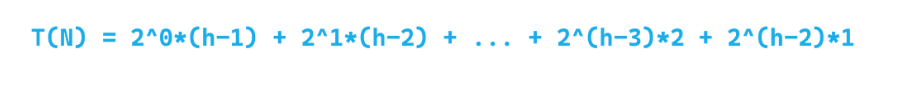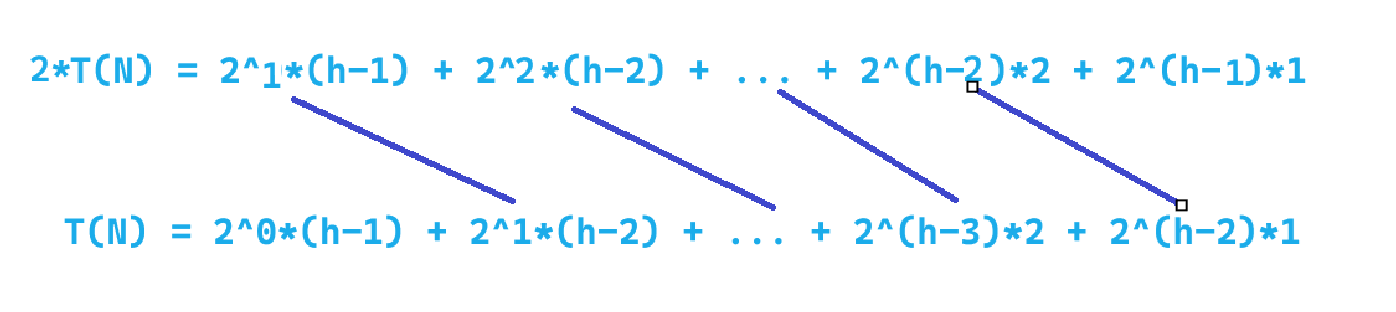[建堆堆排序的时间复杂度推导]向上建堆向下建堆堆排序的时间复杂度分析推导
💖💖💖欢迎来到我的博客,我是anmory💖💖💖
又和大家见面了
欢迎来到动画详解数据结构系列
作为一个程序员你不能不掌握的知识
先来自我推荐一波
个人网站欢迎访问以及捐款
推荐阅读
如何低成本搭建个人网站
专栏:动画详解leetcode算法题
C语言知识
前导知识:求二叉树的节点个数
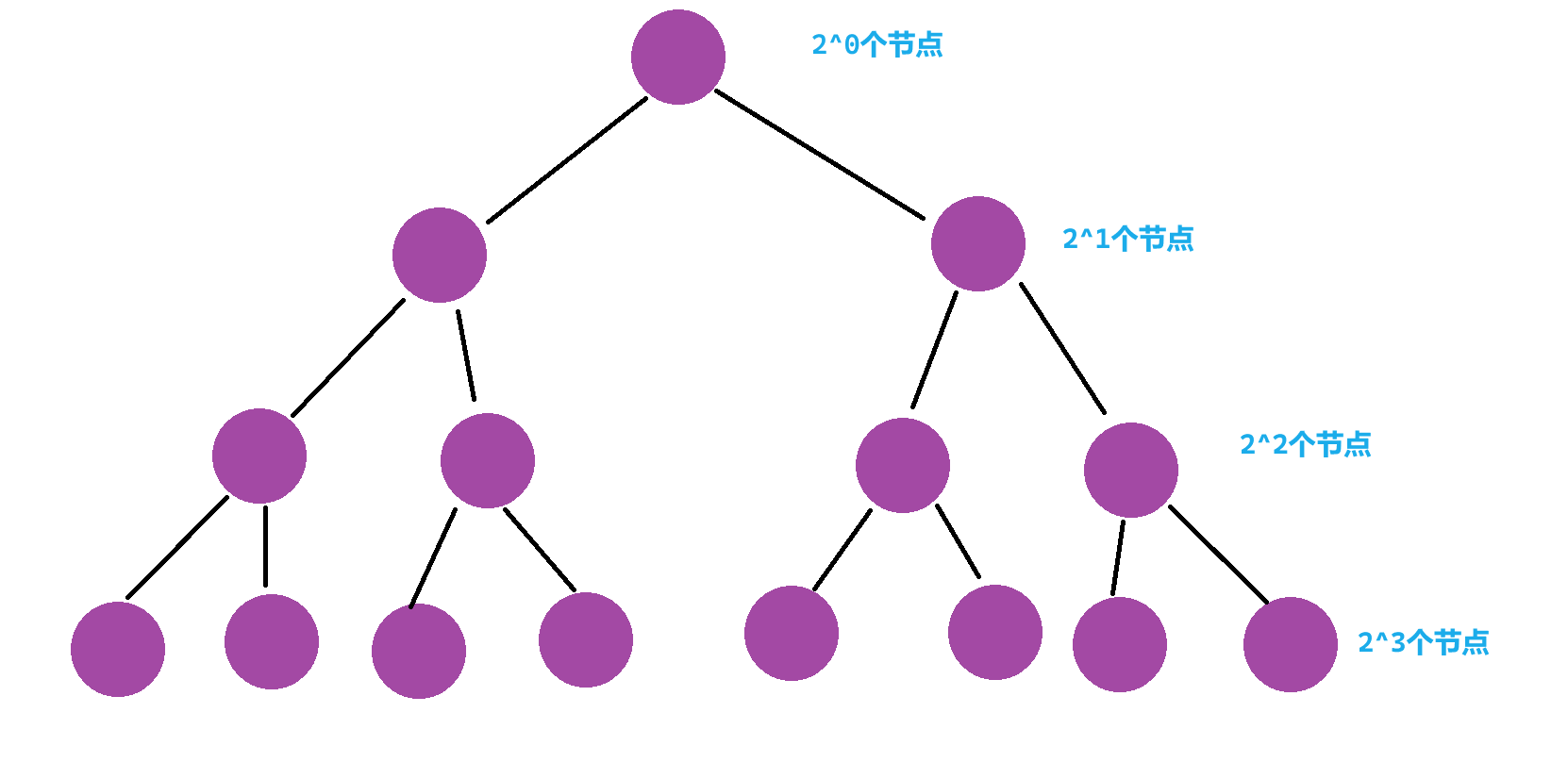
满二叉树的节点个数
对于一个满二叉树,每一层都满足等比数列,所以其节点个数总和我们可以使用等比数列求和公式来计算
我们假设满二叉树的高度是 h h h,节点个数是 N N N
因此,满二叉树的节点个数是 N = 2 h − 1 N = 2^h-1 N=2h−1
满二叉树的高度是 h = l o g 2 ( N + 1 ) h = log_2(N+1) h=log2(N+1)
最后一层只有一个节点的二叉树的节点个数
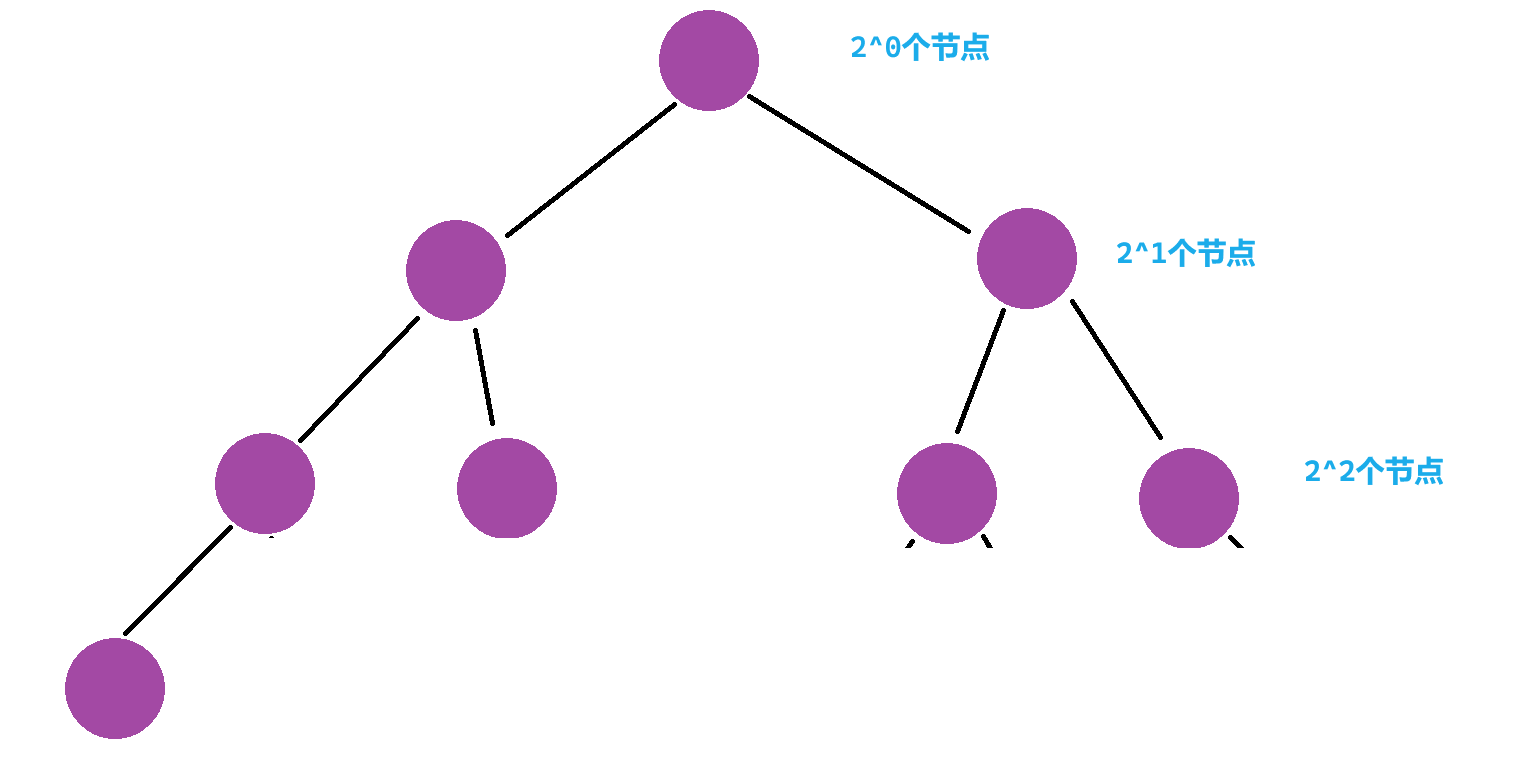
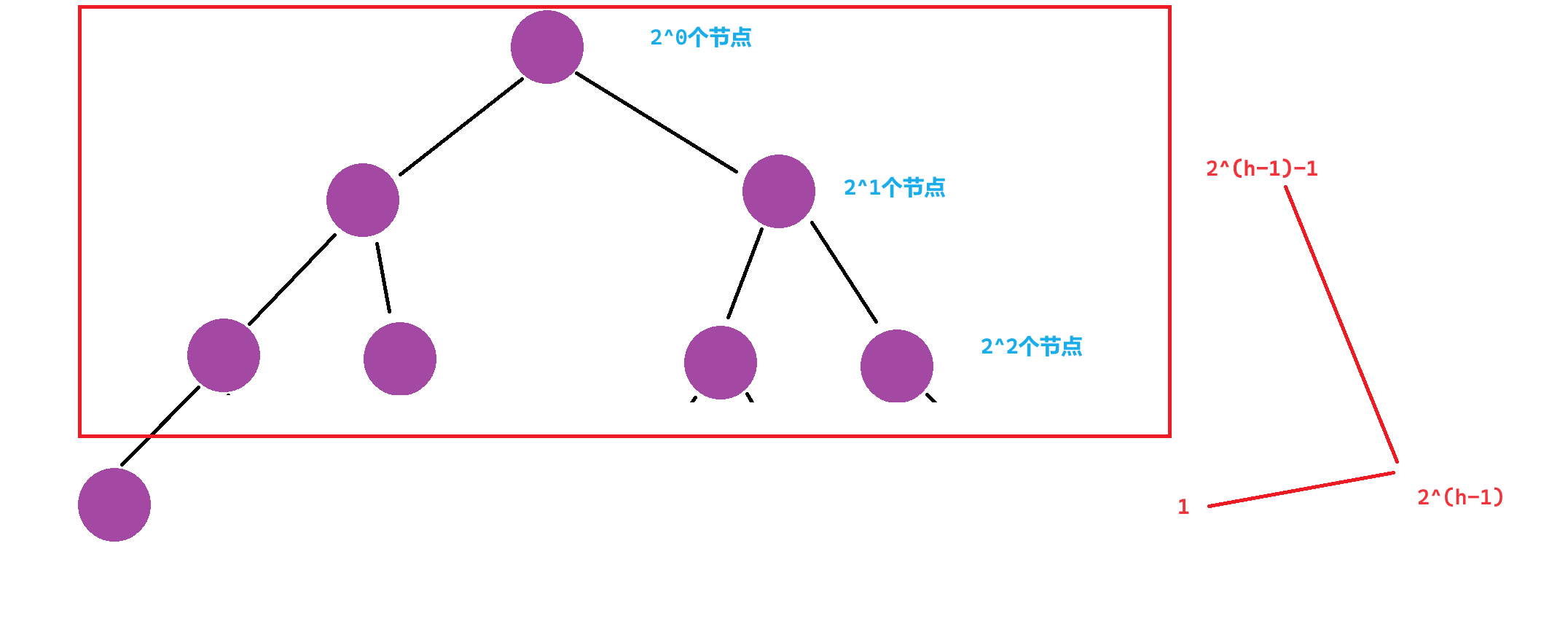
这样的二叉树的节点个数为 N N N= 2^h-1
高度为 h = l o g 2 N h=log_2N h=log2N
向下建堆的时间复杂度推导
向下建堆代码
// 向下调整函数
// n是指堆中有效元素的数量, parent是指堆顶的元素
// 需要比较子节点哪个大哪个小
void AdjustDown(HPDataType* a, int n,int parent)
{// 先假设左孩子大int child = parent * 2 + 1;while (child < n)// 当child>=n时就说明child已经到达叶子节点了{// 先找出左右孩子节点中大的那个if (child + 1 < n && a[child + 1] > a[child])// 说明假设错误,交换小的那个子节点{child++;}// 和父亲节点进行比较if (a[child] > a[parent]){Swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else{break;}}
}
向下建堆的时间复杂度推导
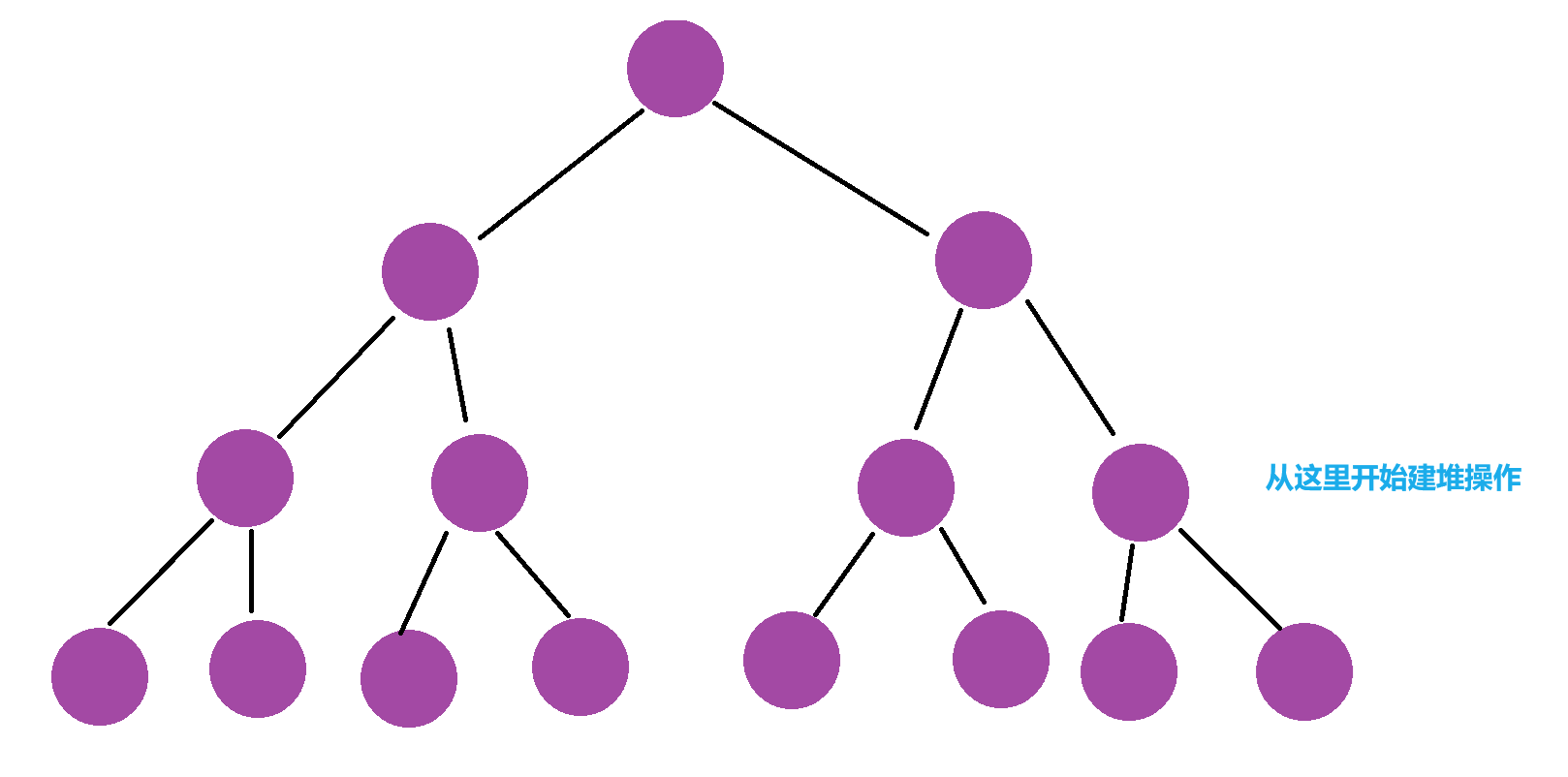
首先我们需要明白的是向下建堆是从倒数第一个非叶子节点开始建堆的
知道了这个之后,我们就可以开始考虑最坏的建堆情况,也就是每一次都要向下调整
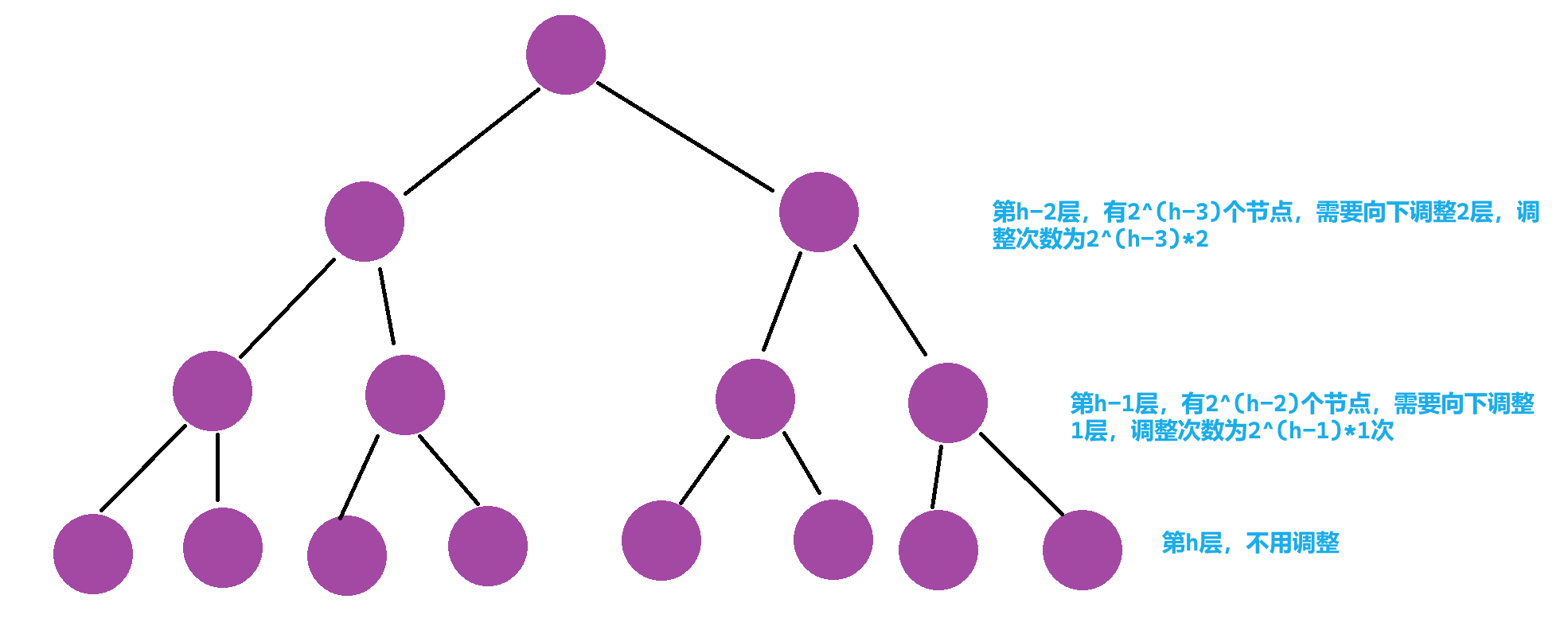
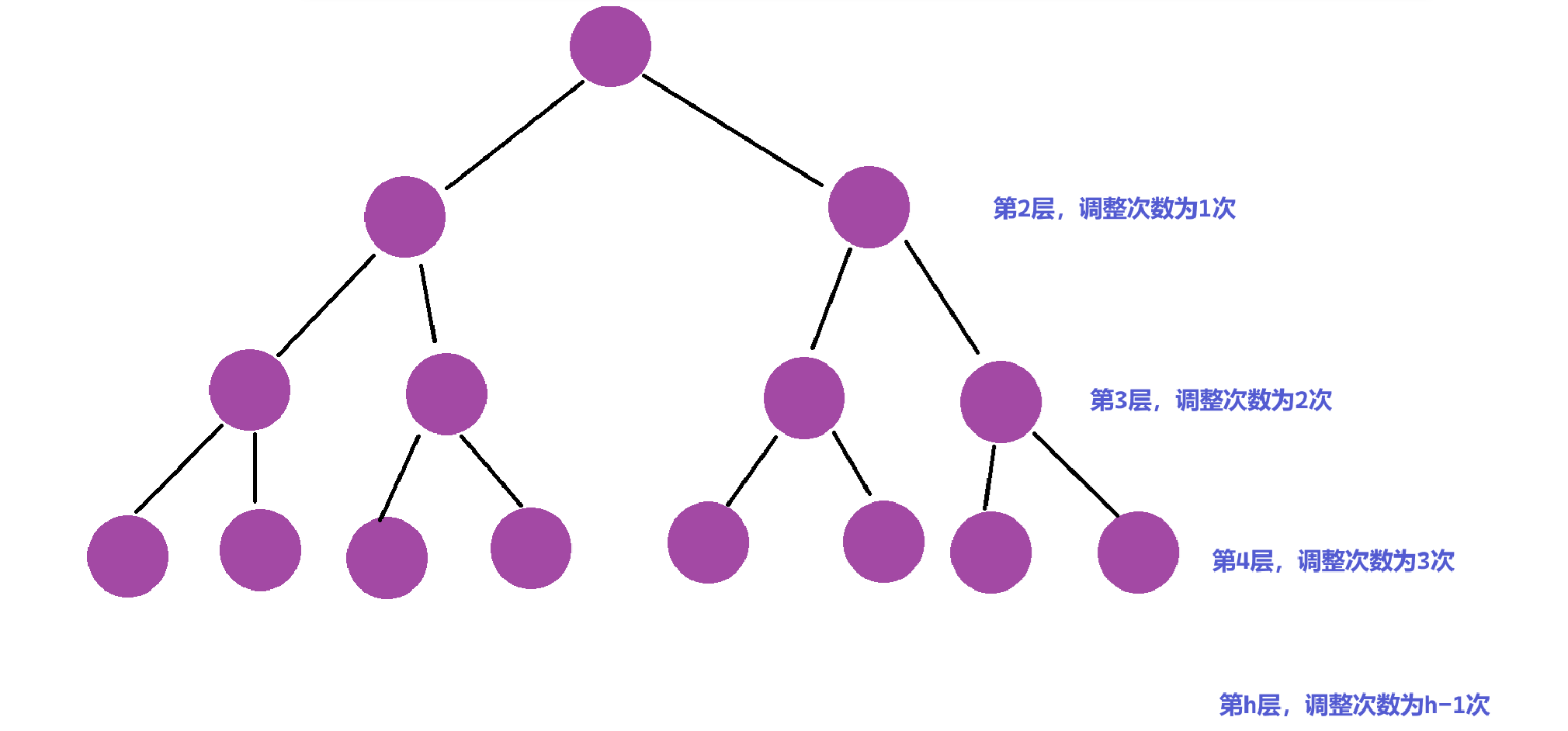
依旧假设高度为 h h h,我们可以算出每一层需要调整的次数
因此我们不难列出总的调整次数的公式
那么,要想算出 T ( N ) T(N) T(N),我们就可以使用错位相减法来对其进行求和
因此,向下调整的总次数为:
因此我们可以得到向下调整建堆的时间复杂度是
O ( N ) O(N) O(N)
除此之外,我们还可以发现
节点数多的调整的次数就少
节点数少的调整的次数就多
向上建堆的时间复杂度推导
向上建堆代码
// 向上调整函数
void AdjustUp(HPDataType* a, int child)
{int parent = (child - 1) / 2;while (child){// 大堆调整if (a[child] > a[parent]){Swap(&a[child], a[parent]);child = parent;parent = (child - 1) / 2;}// 若已经满足大堆,那么就跳出循环else{break;}}
}
向上建堆复杂度推导
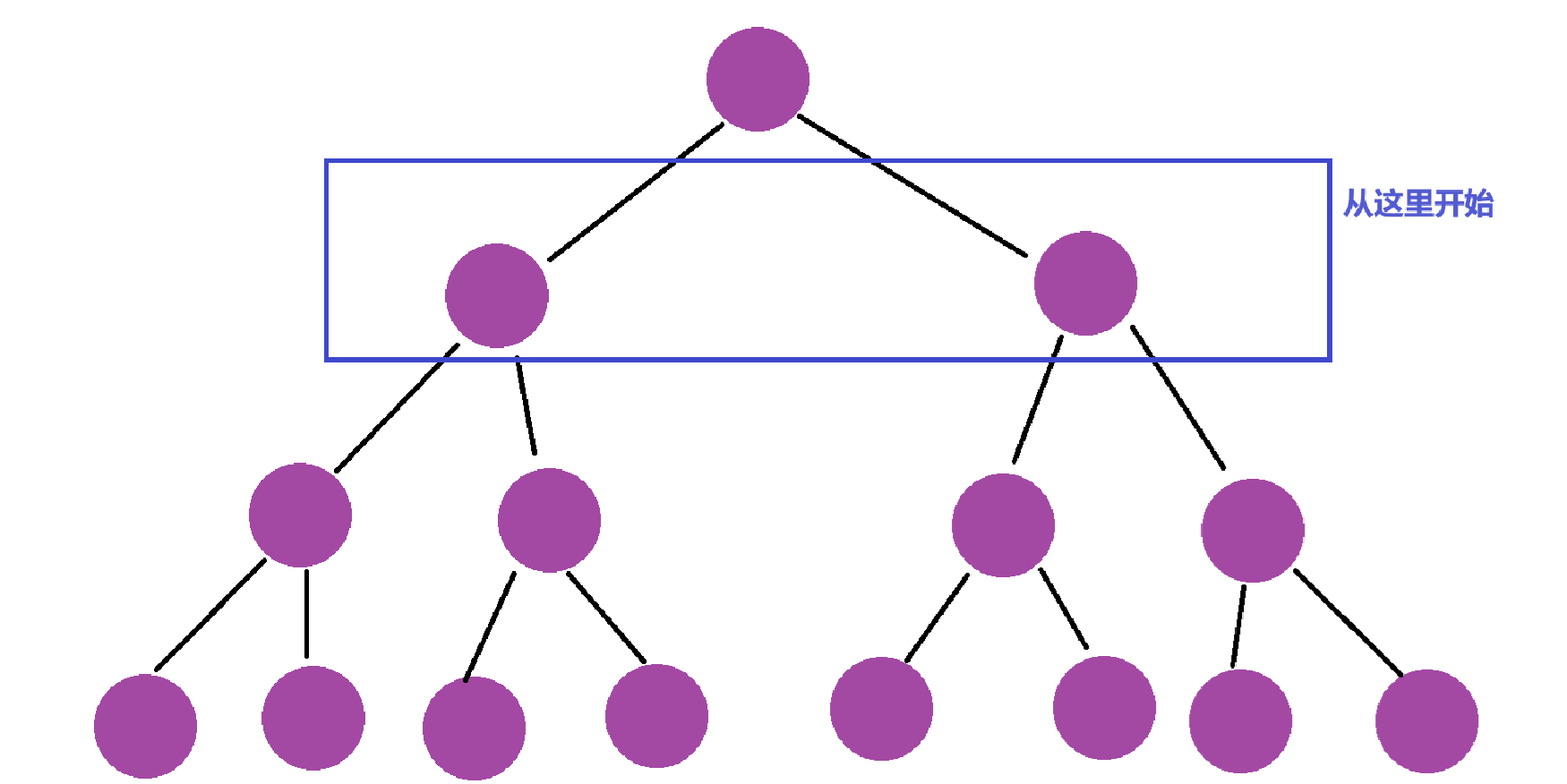
向上调整建堆是从第二层开始的
因此我们可以算出调整的总次数
因此我们可以算出向上调整建堆的时间复杂度为
O ( N l o g N ) O(NlogN) O(NlogN)
除此之外我们可以发现
节点数少的层调整次数少
节点数多的层调整次数多
堆排序的时间复杂度推导
堆排序代码
// 对数组进行堆排序,需要建堆
void HeapSort(int* a, int n)
{// 降序,建小堆// 升序,建大堆for (int parent = (n-1-1)/2; parent > 0; parent--){AdjustDown(a, n, parent);}int end = n - 1;while (end > 0){Swap(&a[0], &a[end]);AdjustDown(a, end, 0);end--;}
}
堆排序的时间复杂度推导
我们可以发现,第一个for循环使用了向下调整建堆,其复杂度为 O ( N ) O(N) O(N)
第二个循环按理来说应该是 O ( N 2 ) O(N^2) O(N2)
但因为第二个循环并非是最坏的情况,所以我们认为其时间复杂度为 O ( N l o g N ) O(NlogN) O(NlogN)
因此,堆排序的时间复杂度就为
O ( N l o g N ) O(NlogN) O(NlogN)
💖💖💖非常感谢各位的支持💖💖💖
我们共同进步
本系列持续更新,关注我,带你了解更多数据结构知识
下期再见