从loss角度理解LLM涌现能力
如今的很多研究都表明小模型也能出现涌现能力,本文的作者团队通过大量实验发现模型的涌现能力与模型大小、训练计算量无关,只与预训练loss相关。
作者团队惊奇地发现,不管任何下游任务,不管模型大小,模型出现涌现能力都不约而同地是在预训练loss降低到 2.2 以下后。
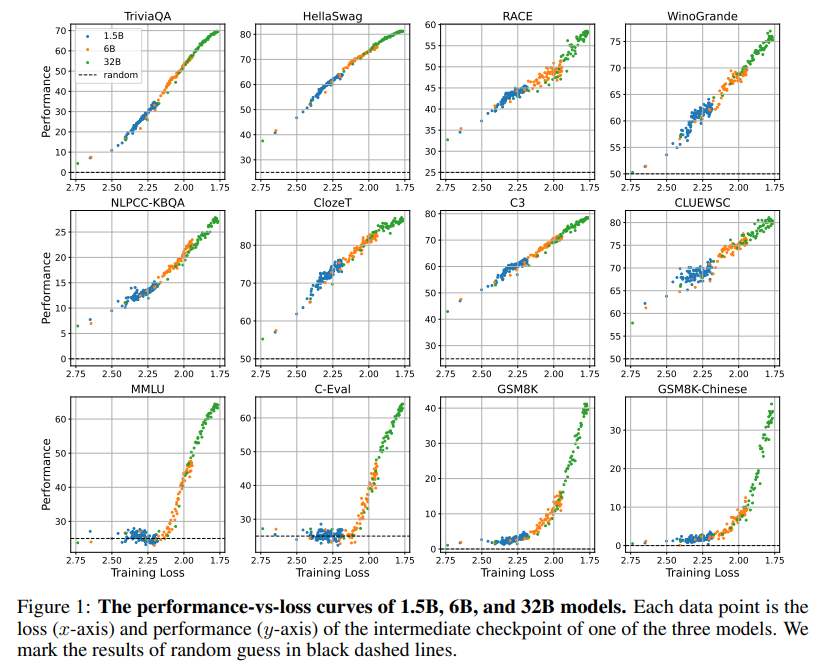
在 2.2 之前,模型的表现跟一般模型无异。在 2.2 之后,模型的性能显著上升。
数学建模
模型涌现能力与预训练loss的关系,公式化如下:
{ f ( L ) if L < η 0 otherwise \begin{cases}f(L) & \text { if } L<\eta \\ 0 & \text { otherwise }\end{cases} {f(L)0 if L<η otherwise
f ( L ) f(L) f(L) 是个单调递减函数, L L L 越大,其值越小。 η \eta η 是个loss阈值,比如 2.2 。
预训练loss与模型大小 N N N 关系如下:
L ( N ) = L ∞ + ( N 0 N ) α N L(N)=L_{\infty}+\left(\frac{N_0}{N}\right)^{\alpha_N} L(N)=L∞+(NN0)αN
因此涌现能力与模型大小的关系如下:
{ f ( L ∞ + ( N 0 N ) α N ) if N ≥ N 0 ⋅ ( η − L ∞ ) − 1 α N 0 otherwise \begin{cases}f\left(L_{\infty}+\left(\frac{N_0}{N}\right)^{\alpha_N}\right) & \text { if } N \geq N_0 \cdot\left(\eta-L_{\infty}\right)^{-\frac{1}{\alpha_N}} \\ 0 & \text { otherwise }\end{cases} {f(L∞+(NN0)αN)0 if N≥N0⋅(η−L∞)−αN1 otherwise
当模型大小超过 N 0 ⋅ ( η − L ∞ ) − 1 α N N_0 \cdot\left(\eta-L_{\infty}\right)^{-\frac{1}{\alpha_N}} N0⋅(η−L∞)−αN1,才会出现涌现能力,否则与普通模型无异。随着模型尺寸变大,预训练loss减少,则模型性能提升。
总结
本文从预训练loss角度观察了模型涌现能力是如何发生的。其结论也给业界评估模型在下游任务上的性能提供了全新的视角,即预训练loss,而不是模型参数量、数据量、训练计算量。
但本文并未从理论角度解释loss与涌现能力的关系,更多地是根据后验进行启发式分析,也未给出 2.2 的合理说明。但DL一直这么玄学,不是吗?
参考
- Understanding Emergent Abilities of Language Models from the Loss Perspective
