数据结构——图的基础知识与其表示
一:图的定义
由顶点的集合和边的集合组成;常以 G(V,E) 表示,G 代表图,V代表 顶点的集合,E代表边的集合;
如图:
在G1图中,有 0~4 五个顶点,有 0-1,0-2,0-4,1-2,2-3,3-4 六条边 ;

二:图的
目录
一:图的定义
二:图的
分类
(1)有/无向图
(2 带/不带权图
三:图的表示
1. 邻接矩阵
1.1 不带权的邻接矩阵:
1.2 带权的邻阶矩阵:
四:实际应用
1.稀疏图
2.稠密图
3.特殊情况
分类
(1)有/无向图
我们根据 边是否有方向分为 有向图,无向图;
如图,无向图中,0可以到1,1也可以到0,0和1之间是等价的;
无向图中,0可以到1,但是1不可以到0;


(2 带/不带权图
我们根据边是否有权重分为带权图,不带权图;
边的度量可以表示时间,距离等具体的量(如G3);
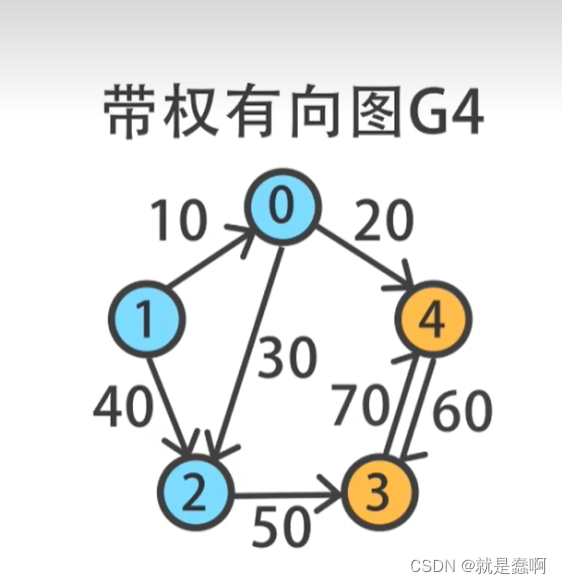
当然,边与边之间的度量可以是不同的(如G4);

三:图的表示
1. 邻接矩阵
即使用二维数据来表示图。
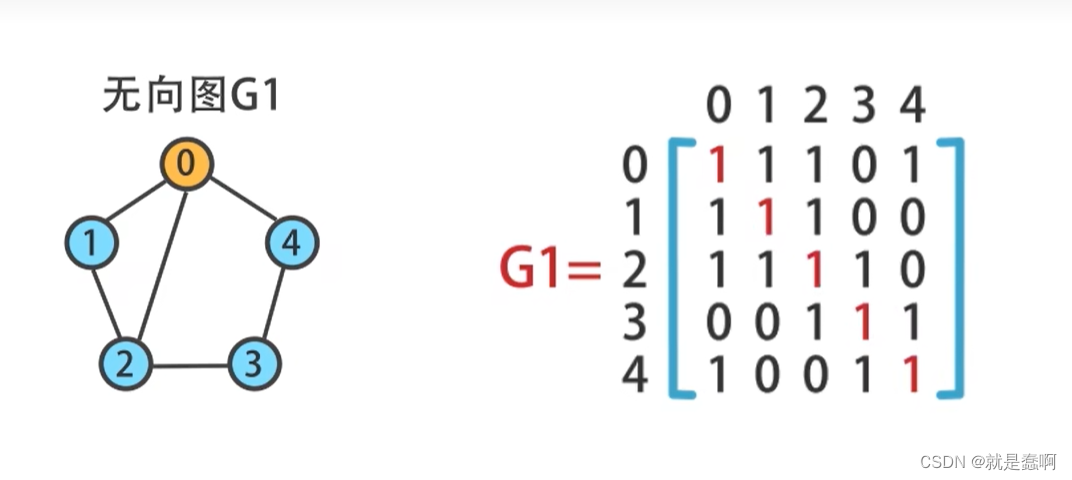
1.1 不带权的邻接矩阵:
1代表两顶点连通,0代表不连通。某顶点带自身的边一般用0表示,

不过,也可以根据需要用 1 表示;
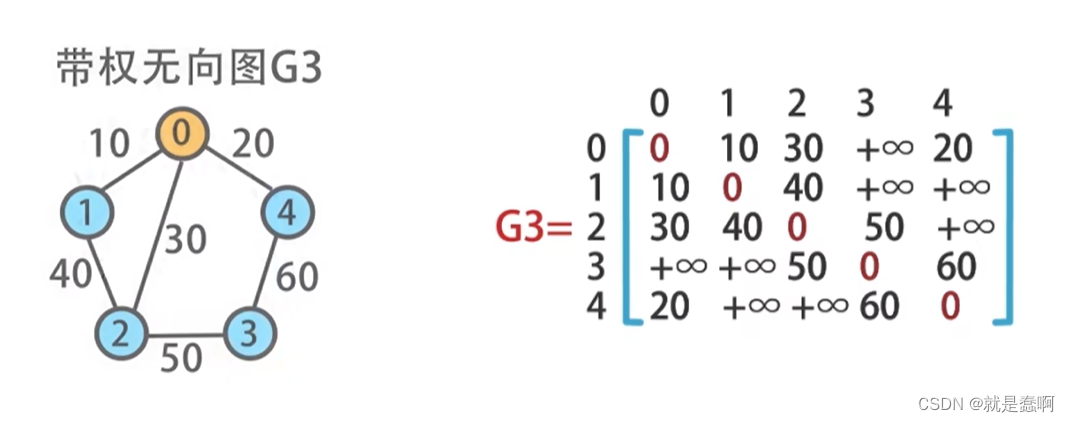
1.2 带权的邻阶矩阵:
顶点之间不连通常用 +∞ 来表示,顶点到自身的边一般标记为 0 ;
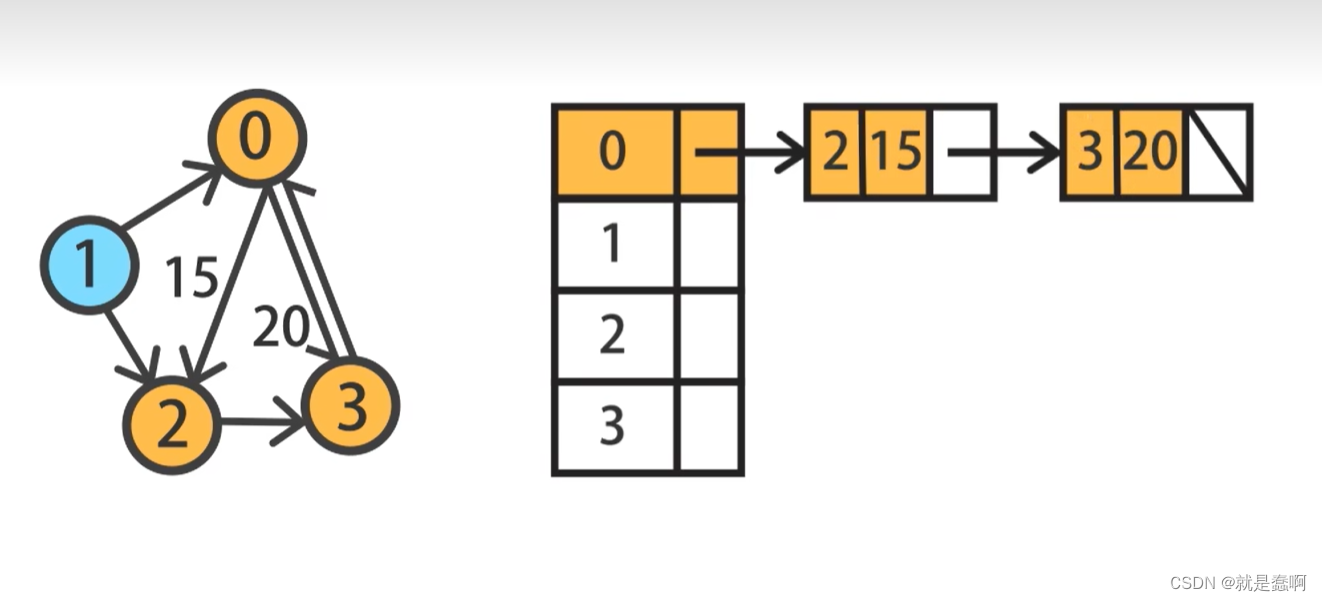
2.邻接表
使用顺序和链式相结合的方式存储图,指针的连接代表相连,与有向还是无向,带权还是不带权无关
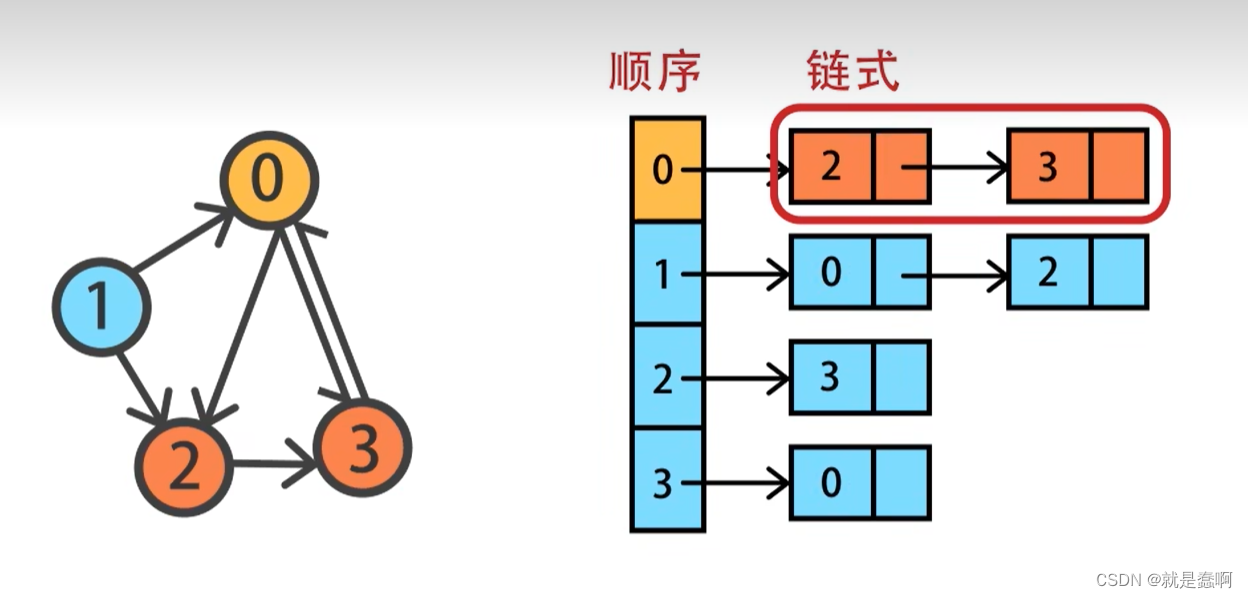
如果需要表示权值的话,我们可以在节点中增加额外的数据域进行存储,
四:实际应用
实际应用时,我们通常根据结点和边的个数来选择邻接矩阵或邻接表来表示图
1.稀疏图
边的条数远远小于顶点的个数:E<<V的平方,选择邻接表,毕竟添加元素方便;
2.稠密图
边的条数远远接近顶点的个数:E 接近 V的平方,选择邻接矩阵;
3.特殊情况
比如我们要判断两个顶点之间是否连通,需要采用邻接矩阵来表示图,因为二维数组遍历的时间复杂度为O(1),这会提高找寻的效率;
