当前位置：首页 > news >正文

【python】模拟巴特沃斯滤波器

news 2025/7/30 10:39:34

巴特沃斯滤波器（Butterworth Filter），以其设计者斯蒂芬·巴特沃斯（Stephen Butterworth）的名字命名，是一种具有平滑频率响应的滤波器。这种滤波器在频域中具有非常平坦的无波纹响应，直到它达到截止频率，之后其响应逐渐下降。巴特沃斯滤波器是滤波器设计中非常受欢迎的一种，尤其是在对信号进行平滑处理时，它们能够最小化相位失真。

巴特沃斯滤波器的特点：

平滑无波纹的响应：在通过带（通带）内，巴特沃斯滤波器具有非常平坦的频率响应，没有切比雪夫滤波器那样的波纹。
最陡峭的过渡带：虽然巴特沃斯滤波器没有切比雪夫滤波器那样的陡峭过渡带，但它提供了平滑的过渡，这在某些应用中是有利的。
相位失真小：巴特沃斯滤波器在通带内的相位失真非常小，这使得它们非常适合于那些对相位失真敏感的应用。
阶数选择：巴特沃斯滤波器的阶数决定了滤波器在截止频率处衰减的速度。阶数越高，滤波器的过渡带就越陡峭，但同时系统将变得更加复杂。

设计参数：

截止频率（cutoff_frequency）：这是滤波器开始显著衰减信号的频率点。在巴特沃斯滤波器设计中，这个频率是归一化的，即相对于Nyquist频率。
滤波器阶数（order）：滤波器的阶数决定了滤波器的性能，包括其在截止频率处的衰减速度。阶数越高，滤波器的性能越好，但计算复杂度也越高。
采样频率（sampling_frequency）：这是信号采样的频率，它决定了Nyquist频率，即采样频率的一半。

应用场景：

巴特沃斯滤波器广泛应用于需要平滑频率响应的场合，例如：

音频和视频信号处理，以去除噪声和干扰。
控制系统中，以实现平滑的信号过渡。
生物医学信号处理，如脑电图（EEG）或心电图（ECG）信号的平滑。

注意事项：

设计巴特沃斯滤波器时，需要在滤波器的性能（如过渡带的陡峭程度）和复杂度（由阶数决定）之间做出权衡。此外，巴特沃斯滤波器在截止频率处的衰减不是最快的，因此在需要快速衰减的应用中可能不是最佳选择。

模拟代码：

import numpy as np
import matplotlib.pyplot as plt
from scipy.signal import butter, freqz# 设计参数
cutoff_frequency = 0.2  # 归一化截止频率（0-1，相对于Nyquist频率）
order = 5  # 滤波器的阶数
sampling_frequency = 2 * np.pi  # 采样频率，与Nyquist频率一致# 计算归一化截止频率
nyquist_freq = sampling_frequency / 2
norm_cutoff = cutoff_frequency / nyquist_freq# 计算滤波器系数
b, a = butter(order, norm_cutoff, btype='low', analog=False)# 计算滤波器的频率响应
freq, response = freqz(b, a, 1000)# 将频率转换为Hz
freq_hz = freq * (0.5 / np.pi)# 绘制幅频响应
plt.figure(figsize=(10, 8))
plt.plot(freq_hz, 20 * np.log10(np.abs(response)), label='Butterworth Lowpass Filter')# 添加图例
plt.legend()# 添加标题和轴标签
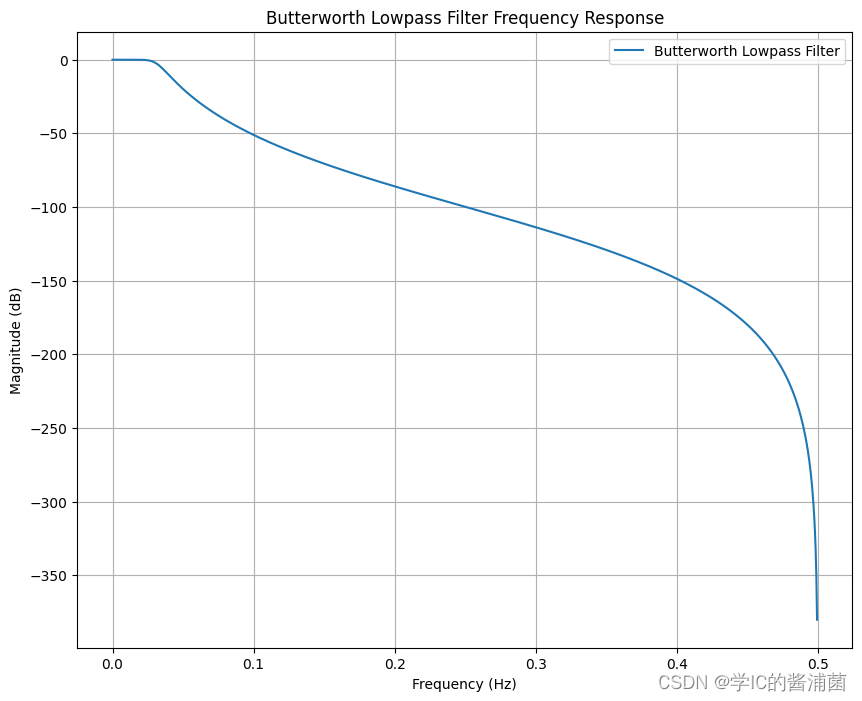
plt.title('Butterworth Lowpass Filter Frequency Response')
plt.xlabel('Frequency (Hz)')
plt.ylabel('Magnitude (dB)')# 显示网格
plt.grid(True)# 显示图像
plt.show()