Eigen求解线性方程组
1、线性方程组的应用
线性方程组可以用来解决各种涉及线性关系的问题。以下是一些通常可以用线性方程组来解决的问题:
在实际工程和科学计算中,求解多项式方程的根有着广泛的应用。
在控制系统的设计中,我们经常需要求解特征方程的根来分析系统的稳定性;
在图像处理和模式识别中,多项式方程的根可以用来寻找图像的特征点;
在金融工程和风险管理中,多项式方程的根可以用来对数据进行拟合和预测。
-
工程问题:工程领域中存在大量的线性关系问题,例如:
- 结构力学:求解结构物体系的平衡状态。
- 电路分析:计算电路中的电流、电压等。
- 控制系统:建立控制系统的数学模型,进行分析和设计。
-
物理问题:物理学中很多问题都可以归结为线性方程组,例如:
- 运动学和动力学:描述物体在运动过程中的位移、速度、加速度等。
- 电磁学:描述电场、磁场的分布和相互作用。
- 热传导:描述热量在物体内部传递和分布的过程。
-
优化问题:很多优化问题可以转化为线性方程组求解的问题,例如:
- 线性规划:通过线性方程组求解目标函数的最优值。
- 最小二乘法:拟合数据点到一个线性函数或者多项式,使得残差平方和最小化。
-
数据分析:数据分析中经常需要拟合数据、估计参数等,这些问题通常可以转化为线性方程组的形式来求解。
-
金融领域:金融领域中的风险评估、资产定价等问题也可以用线性方程组来描述和求解。
-
机器学习和模式识别:很多机器学习算法和模式识别方法涉及到解决线性方程组,例如:
- 线性回归:建立线性模型来预测或拟合数据。
- 支持向量机:求解超平面来进行分类。
2、Eigen求解线性方程组
Eigen提供了多种方法来求解线性方程组,具体取决于方程组的特性、稀疏程度以及性能需求。以下是Eigen中常用的一些线性方程组求解方法:
-
直接解法:
- LU分解:通过LU分解(或者部分选主元LU分解)来求解稠密矩阵的线性方程组。
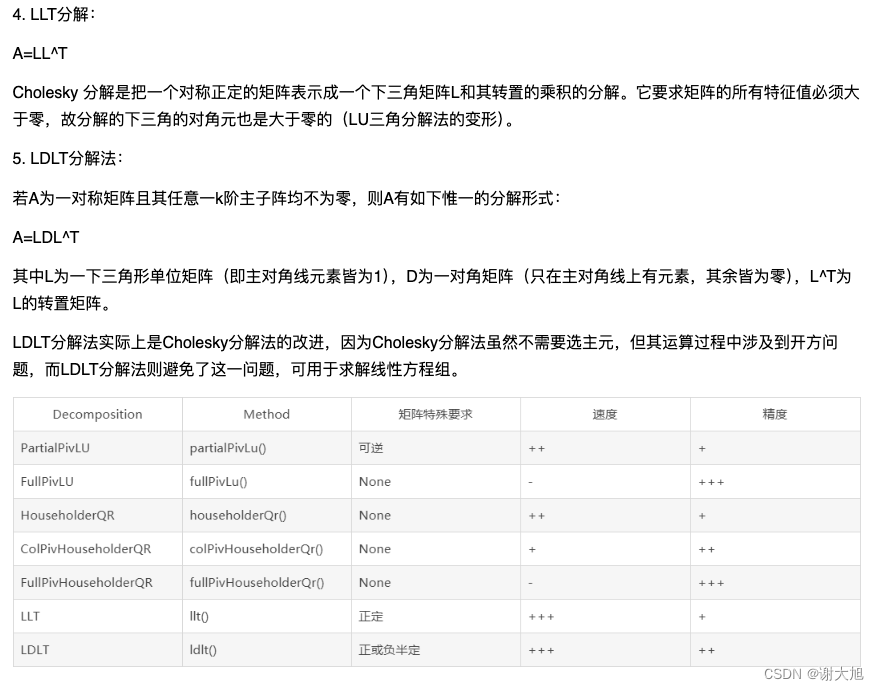
- LLT分解:用于对称正定矩阵的Cholesky分解。
- LDLT分解:用于对称矩阵的LDLT分解。
-
迭代法:
- Jacobi迭代法
- Gauss-Seidel迭代法
- Successive Over-Relaxation (SOR)迭代法
- Conjugate Gradient (CG)方法:用于对称正定矩阵的迭代法。
- BiCGSTAB方法:用于一般非对称矩阵的迭代法。
- GMRES方法:广义最小残差法,用于非对称矩阵的迭代法。
-
QR分解:通过QR分解求解线性方程组,例如使用Householder QR分解或者ColPivHouseholderQR分解。
-
SVD分解:使用奇异值分解(Singular Value Decomposition)来求解最小二乘问题或者解决非方阵的线性方程组。
-
稀疏矩阵求解:对于稀疏矩阵,Eigen也提供了一些特定的求解器,如BiCGSTAB、SparseLU等。
每种方法都有其适用范围和性能特点,选择合适的方法取决于线性方程组的特性以及求解的需求(例如精度、速度、稀疏性等)。Eigen提供了丰富的线性方程组求解功能,可以根据具体情况选择最合适的方法。
2、线性方程组的构造
这个需要另外写一篇博客总结下什么问题可以用线性方程组来建模。下一篇就来学习下Eigen在orb-slam2中的应用。
3、参考文献

eigen稀疏矩阵求逆 - 百度文库 (baidu.com)
