二分图(染色法与匈牙利算法)
二分图当且仅当一个图中不含奇数环
1.染色法
简单来说,将顶点分成两类,边只存在于不同类顶点之间,同类顶点之间没有边。
e.g.
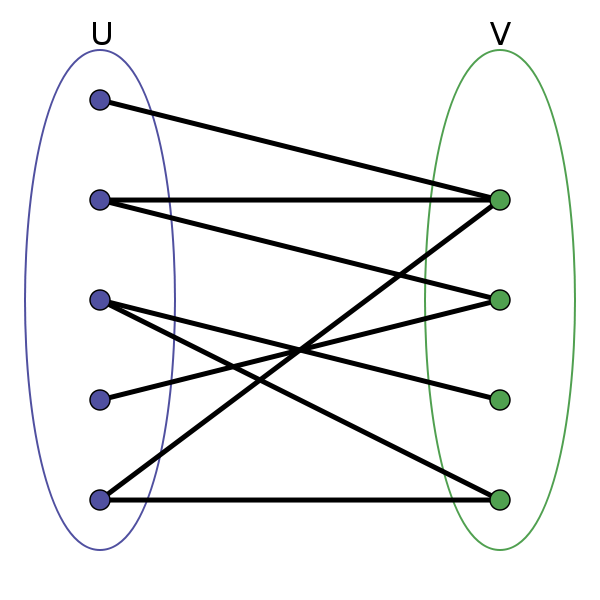
如果判断一个图是不是二分图?
开始对任意一未染色的顶点染色。
判断其相邻的顶点中,若未染色则将其染上和相邻顶点不同的颜色。
若已经染色且颜色和相邻顶点的颜色相同则说明不是二分图,若颜色不同则继续判断。
bfs和dfs可以搞定!
注意:如果有三个点另外成环,整个环是一个孤立环,其他都满足二分图,但是这个孤立不满足二分图,二分图的点不一定连通。所以要遍历每一个点。
1.dfs思路:
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N=200010;
int e[N], ne[N], idx;//邻接表存储图
int h[N];
int n,m;
int color[N];
void add(int a, int b)//邻接表插入点和边
{e[idx] = b, ne[idx]= h[a], h[a] = idx++;
}
bool dfs(int a,int c){color[a]=c;for(int i=h[a];i!=-1;i=ne[i]){int j=e[i];if(!color[j]){if(!dfs(j,3-c)){return false;}}else{if(color[j]==c){return false;}}}return true;
}
int main(){memset(h, -1, sizeof h);//初始化邻接表cin >> n >> m;for(int i = 1; i <= m; i++)//读入边{int a, b;cin >> a >> b;add(a, b), add(b, a);}for(int i=1;i<=n;i++){if(!color[i]){if(!dfs(i,1)){puts("No");return 0;}}}puts("Yes");return 0;
}2.bfs思路:
#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
using namespace std;
const int N=200010;
int e[N], ne[N], idx;//邻接表存储图
int h[N];
int n,m;
int color[N];queue<int> q;
void add(int a, int b)//邻接表插入点和边
{e[idx] = b, ne[idx]= h[a], h[a] = idx++;
}
bool bfs(int a){color[a]=1;q.push(a);while(q.size()){auto t=q.front();q.pop();for(int i=h[t];i!=-1;i=ne[i]){int j=e[i];if(!color[j]){color[j]=3-color[t];q.push(j);}else if(color[j]==color[t]) return false;}}return true;
}
int main(){memset(h, -1, sizeof h);//初始化邻接表cin >> n >> m;for(int i = 1; i <= m; i++)//读入边{int a, b;cin >> a >> b;add(a, b), add(b, a);}for(int i=1;i<=n;i++){if(!color[i]){if(!bfs(i)){puts("No");return 0;}}}puts("Yes");return 0;
}2.匈牙利算法
要了解匈牙利算法必须先理解下面的概念:
匹配:在图论中,一个「匹配」是一个边的集合,其中任意两条边都没有公共顶点。
最大匹配:一个图所有匹配中,所含匹配边数最多的匹配,称为这个图的最大匹配。
这篇文章把这个算法讲的很有意思:
趣写算法系列之--匈牙利算法_匈牙利算法基本原理-CSDN博客
简单来说就是:
遍历所有男生
让该男生考虑所有心动女生
如果当前女生单身,或者该女生的对象找了备胎,该女生就接受该男生
最坏时间复杂度 O(nm),和其它最大流问题一样,实际比较快
#include <cstring>
#include <iostream>
#include <algorithm>using namespace std;const int N = 510, M = 100010;int n1, n2, m;
int h[N], e[M], ne[M], idx;
int match[N];
bool st[N];void add(int a, int b)
{e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}
bool find(int x){for(int i=h[x];i!=-1;i=ne[i]){int j=e[i];if(!st[j]){st[j]=1;if(match[j]==0||find(match[j])){match[j]=x;return true;}}}return false;
}
int main()
{scanf("%d%d%d", &n1, &n2, &m);memset(h, -1, sizeof h);while (m -- ){int a, b;scanf("%d%d", &a, &b);add(a, b);}int res = 0;for (int i = 1; i <= n1; i ++ ){memset(st, false, sizeof st);if (find(i)) res ++ ;}printf("%d\n", res);return 0;
}在上述代码中,有一个令人费解的东西:就是st数组的作用,其实直白的理解:如果你每次不把st重新置为false,那剩下的人一看到前面的妹子st已经为true,不去让妹子的对象换掉这个妹子,直接就放弃了,会影响最后结果。
我们通过一个实际案例理解一下:
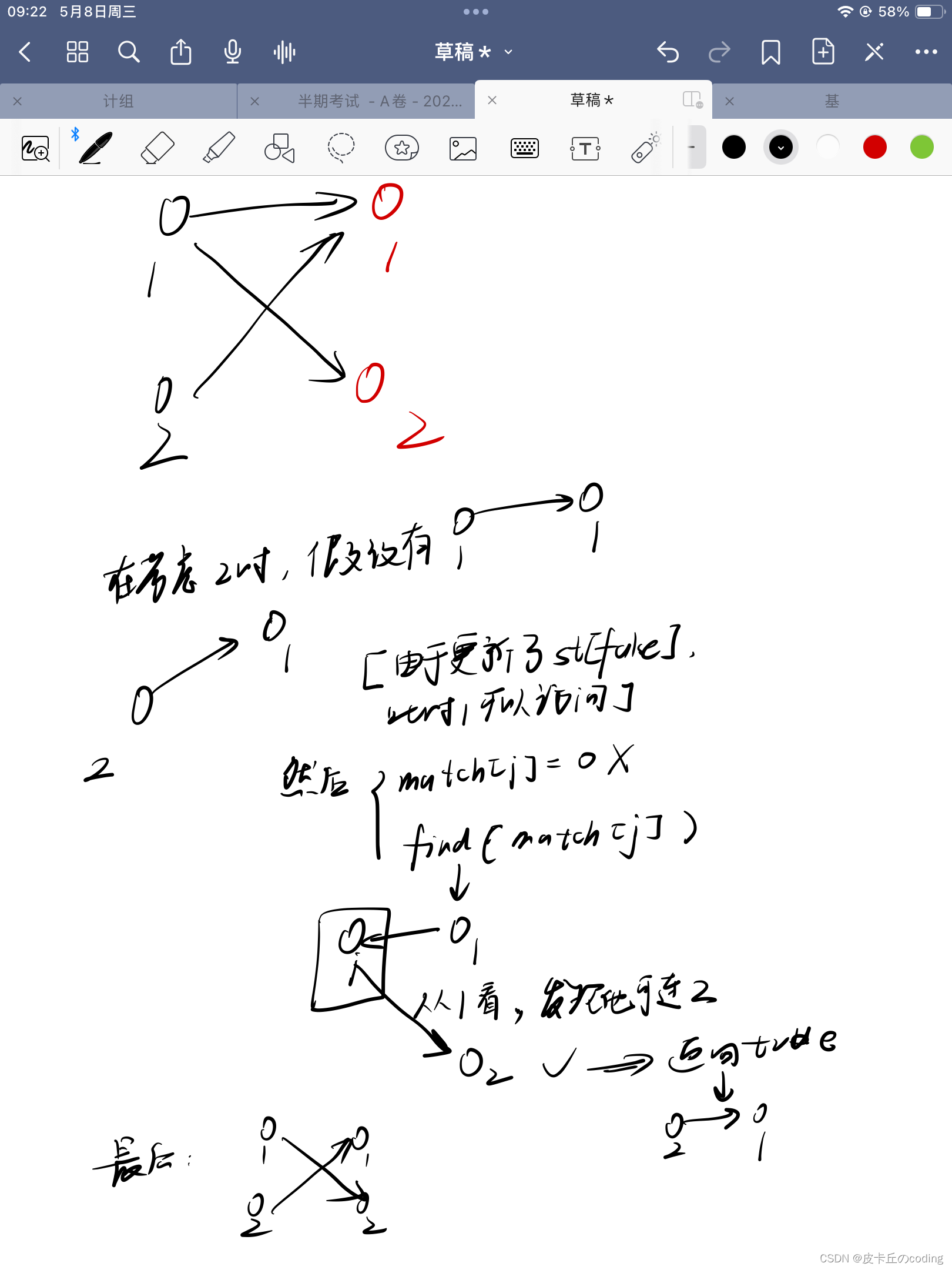
不难看出,st数组主要是在两个人连接了一个妹子的的时候才有用, 这个st的存在,让find在本次找的时候,原来的那个男生,不会再找这个妹子,只会找其他的。
还有一种理解:st的理解可以参考操作系统中锁的概念。假如说左边的是进程,右边的是资源。当进程i要访问资源j时,为了避免其他进程在此时访问资源j,需要对资源j加一个“锁”,即st[j] = true。当进程i访问完资源时,为了让后续其他进程也能访问资源,需要把锁解开,即memset(st, false, sizeof st)。
