二叉树的遍历(前序、中序、后序)| C语言

目录
0.写在前面
1.前序遍历
步骤详解
代码实现
2.中序遍历
步骤详解
代码实现
3.后序遍历
步骤详解
代码实现
0.写在前面
认识二叉树结构最简单的方式就是遍历二叉树。所谓遍历二叉树就是按照某种特定的规则,对二叉树的每一个节点进行访问,且每个节点只访问一次。
二叉树遍历的规则一般有四种:前序遍历、中序遍历、后序遍历和层序遍历。其中,前三种较为简单且实现方式大同小异。
1.前序遍历:先访问根节点,再遍历左右子树;
2.中序遍历:先遍历左子树,再访问根节点,再遍历右子树;
3.后序遍历:先遍历左子树,再遍历右子树,再访问根节点。
简单记忆:前(根,左,右)、中(左,根,右)、后(左,右,根)。
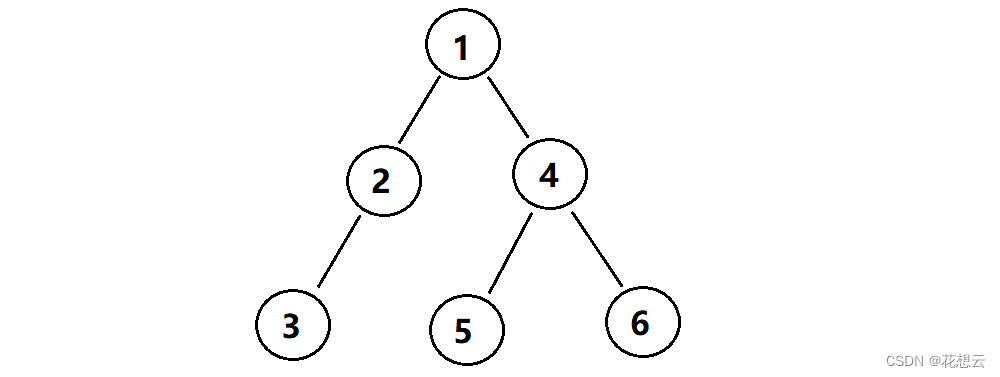
在遍历二叉树之前,首先得拥有一棵二叉树。因为目前还没有学习如何构建二叉树,所以此处我们用最原始的办法——申请N个节点,将它们手动拼接为二叉树。
typedef int BTDataType;//二叉树节点的结构
typedef struct BTNode
{BTDataType data;struct BTNode* left;struct BTNode* right;
}BTNode;//定义一个申请新节点的函数
BTNode* BuyBTNode(BTDataType data)
{BTNode* newNode = (BTNode*)malloc(sizeof(BTNode));if (newNode == NULL){perror("malloc fail");exit(-1);}newNode->data = data;newNode->left = NULL;newNode->right = NULL;return newNode;}int main()
{//手动申请节点加连接BTNode* n1 = BuyBTNode(1);BTNode* n2 = BuyBTNode(2);BTNode* n3 = BuyBTNode(3);BTNode* n4 = BuyBTNode(4);BTNode* n5 = BuyBTNode(5);BTNode* n6 = BuyBTNode(6);n1->left = n2;n1->right = n4;n2->left = n3;n4->left = n5;n4->right = n6;return 0;
}
1.前序遍历
前序遍历:先访问根节点,再访问左子树,再访问右子树;
void PrevOrder (BTNode* root)为了更好的理解前序遍历的规则,接下来展示一下详细步骤。
步骤详解
1.先访问根节点 (data = 1),再访问左子树;
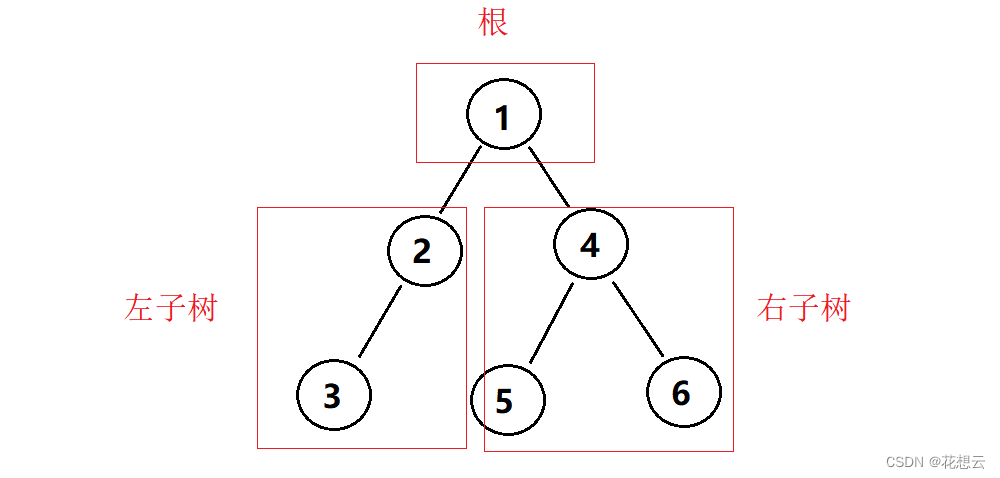
2.再访问左子树的根节点(data = 2),再访问左子树的左子树;

3.依旧先访问根节点(data = 3),此时 n3 节点的左右子树都为 NULL ,则不再往下递归,回到上一层;接着访问上一层的右子树;

4.因为 n2 节点的右子树为 NULL,所以继续返回上一层;访问上一层的右子树;

5.访问右子树的根节点(data = 4),再访问右子树的左子树;先左子树的根节点(data = 5),n5 节点的左右子树都为 NULL,返回上一层访问右子树(data = 6),同样 n6 节点的左右子树都为 NULL,返回上一层。
至此每个节点都访问完毕,总体的访问顺序是这样的:

按照访问顺序打印的结果应该是(空节点用 NULL 表示):
1 2 3 NULL NULL NULL 4 5 NULL NULL 6 NULL NULL 代码实现
按照前序遍历的逻辑,前序遍历的实现肯定是离不开递归。
void PrevOrder(BTNode* root)
{if (root == NULL){ printf("NULL ");//空节点用 NULL 表示return; }printf("%d ", root->data);//前序在前PrevOrder(root->left);PrevOrder(root->right);
}
(凑合着看,有点丑陋hhhhh)
运行程序,看结果是否与之前推理的结果一致:
int main()
{//手动申请节点加连接BTNode* n1 = BuyBTNode(1);BTNode* n2 = BuyBTNode(2);BTNode* n3 = BuyBTNode(3);BTNode* n4 = BuyBTNode(4);BTNode* n5 = BuyBTNode(5);BTNode* n6 = BuyBTNode(6);n1->left = n2;n1->right = n4;n2->left = n3;n4->left = n5;n4->right = n6;PrevOrder(n1);return 0;
}//推理结果
1 2 3 NULL NULL NULL 4 5 NULL NULL 6 NULL NULL 
2.中序遍历
前中后序三种遍历大同小异,实现代码也几乎相同。
void InOrder(BTNode* root)步骤详解
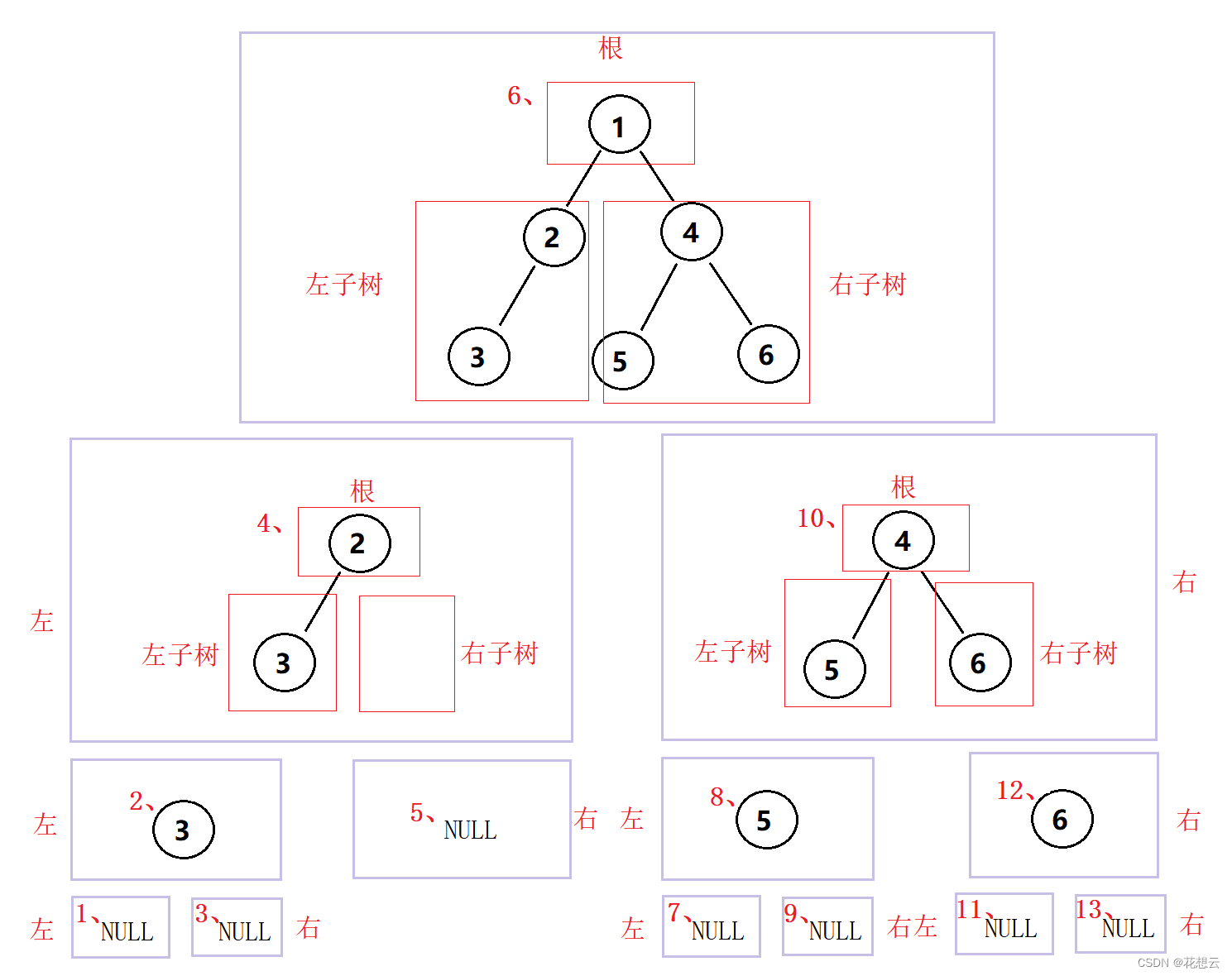
代码实现
void InOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}PrevOrder(root->left);printf("%d ", root->data);//中序在中PrevOrder(root->right);
}//推理结果
NULL 3 NULL 2 NULL 1 NULL 5 NULL 4 NULL 6 NULL
3.后序遍历
步骤详解
参考1、2。
代码实现
void PostOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}PostOrder(root->left);PostOrder(root->right);printf("%d ", root->data);//后序在后
}
