堆放砖块-第12届蓝桥杯选拔赛Python真题精选

[导读]:超平老师的Scratch蓝桥杯真题解读系列在推出之后,受到了广大老师和家长的好评,非常感谢各位的认可和厚爱。作为回馈,超平老师计划推出《Python蓝桥杯真题解析100讲》,这是解读系列的第47讲。
堆放砖块,本题是2021年1月23日举办的第12届蓝桥杯青少组Python编程选拔赛真题,题目要求编程计算按照一定规律进行堆放砖块的总数量。
先来看看题目的要求吧。
一.题目说明
提示信息:
有一堆砖,需要按照一定规律进行堆放,具体堆放规律如下:
顶层放1块砖,
第二层放3块砖,
第三层放6块砖,
第四层放10块砖,
......
依此类推,每一层砖块的数量为上一层砖块数量加上本层的层数。例如第五层为10 + 5 = 15。
输入砖块堆放的总层数,按照以上规律,求出砖块的总数。
编程实现:
输入砖块堆放的总层数,按照以上堆放规律,求出砖块的总数。
例如:输入为3,总层数为3层的砖块堆放一共有1 + 3 + 6 = 10块砖,则输出10。
输入描述:
输入一个正整数N(2 < N < 1000)作为砖块堆放的总层数
输出描述:
输出砖块的总数
样例输入:
3
样例输出:
10
二.思路分析
这是一道简单的计算题,考查的知识点主要是循环和变量。
古希腊毕达哥拉斯学派提出“万物皆数”,他们很重视数学,企图用数来解释一切。公元前6世纪,毕达哥拉斯学派在研究数的概念时,常常把数描绘成沙滩上的小石子,用它们进行各式各样的排列和分类,叫做“形数”。
他们发现数目为1,3,6,10,15,21……这些数量的石子,都可以排成三角形,像这样的数称为三角形数。
例如,前4个三角形数可以排成如下三角形:
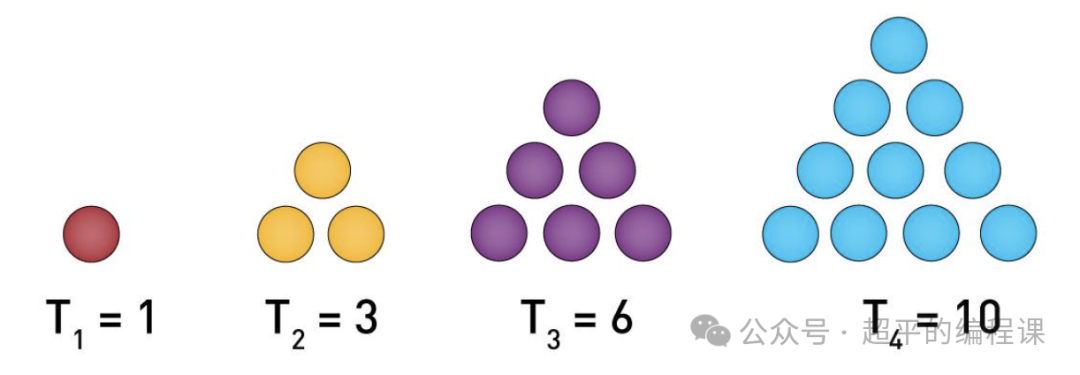
题目中的堆放砖块规律和三角形数完全一样,我们需要分析数字的增长规律,分析过程如下:
T2 - T1 = 3 - 1 = 2T3 - T2 = 6 - 3 = 3T4 - T3 = 10 - 6 = 4T5 - T4 = 15 - 10 = 5......
不难发现,前后两项的差是一个自然数列,在数学中这种数列被称作二级等差数列,或者差等差数列。
对于二级等差数列问题,典型的思路就是设置一个变量表示公差,在循环过程中不断地改变公差,这样就可以计算出每一项的值。
思路有了,接下来,我们就进入具体的编程实现环节。
三.编程实现
根据上面的思路分析,我们编写程序如下:

代码不多,强调两点:
1). 这里的a表示当前层的砖块数量,d表示公差,s表示总和,循环时,首先将当前层的砖块a进行累加,然后增加公差,再计算出下一层的砖块数量;
2). 由于第2层和第1层相差为2,所以将公差d的初始值设为1,并在循环中先将公差加1,再计算砖块数量,当然你也可以设置为不同的初始值和顺序,只要确保公差从2开始增加即可。
至此,整个程序就全部完成了,你也可以输入不同的层数来测试效果。
四.总结与思考
本题代码在10行左右,涉及到的知识点包括:
-
循环语句,主要for...in循环;
-
输入输出;
-
变量的使用;
本题难度一般,属于典型的循环累加题目。关键在于如何找到砖块递增的规律,从而计算出每一层的砖块数量,然后进行累加。
在实际比赛时,很多同学会遇到两个小麻烦,一是找不到砖块增加的规律,二是找到了规律,但不知道如何计算每一层的砖块。
针对对一个问题,说明平时在数学课上练习得不够。实际上,在小学二、三年级的课本中,有大量的数列找规律题目,比较典型的有等差数列、等比数列和斐波那契数列。
对于第二个问题,还是要灵活运用计算思维中的拆分思想,将复杂问题分解成多个简单的问题。由于每一层的砖块数量不能直接得出,不妨使用变量表示,先计算出每一层的砖块数量,然后考虑累加问题,如此一来,问题就变简单了。
超平老师给你留一道思考题,除了三角形数,你还知道有哪些其它形数吗,它们又有什么样的特点呢?
你还有什么好的想法和创意吗,也非常欢迎和超平老师分享探讨。
如果你觉得文章对你有帮助,别忘了点赞和转发,予人玫瑰,手有余香😄
需要源码的,可以移步至“超平的编程课”gzh。
