leetcode热题100.爬楼梯(从二进制到快速幂)
Problem: 70. 爬楼梯
文章目录
- 题目
- 思路
- Code
- 复杂度
题目
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
示例 1:
输入:n = 2
输出:2
解释:有两种方法可以爬到楼顶。
1 阶 + 1 阶
2 阶
示例 2:
输入:n = 3
输出:3
解释:有三种方法可以爬到楼顶。
- 1 阶 + 1 阶 + 1 阶
- 1 阶 + 2 阶
- 2 阶 + 1 阶
思路
在上一讲从递归到动态规划中,我们讲解了递归和动态规划的求解思路,但是我们发现这两种方案的时间复杂度都为 o ( n ) o(n) o(n),我们试图找一种更加优秀的时间复杂度的解法
这里我们就要介绍快速幂的概念了
我们先将n表现为2进制,例如 3 13 3^{13} 313 = 3 1101 3^{1101} 31101 = 3 8 3^8 38 * 3 4 3^4 34 * 3 3 3
因为n有 ⌊ l o g 2 n ⌋ \lfloor log_2n \rfloor ⌊log2n⌋+1 个二进制位 当我们知道了 a 1 , a 2 , a 3 . . . . a^1,a^2,a^3.... a1,a2,a3....后我们只需要 o ( l o g n ) o(log n) o(logn)次乘法就可以计算出 a n a^n an了。
于是我们只需要知道一个快速的方法来计算上述 3 的 2 k 2^k 2k 次幂的序列。这个问题很简单,因为序列中(除第一个)任意一个元素就是其前一个元素的平方。例如:

那么对于我们刚才举得例子而言,我们只要计算得出 3 8 3^8 38 , 3 4 3^4 34 , 3 3 3,就可以得到其最后的真实值。
整个算法的时间复杂度是 0 ( l o g n ) 0(logn) 0(logn),比递归和递归都要优秀
回到本题,本题快速乘有一点不同,本题要用到矩阵 ,由上一篇从递归到动态规划中,我们已经知道了状态的递归公式:
f ( n ) = f ( n − 1 ) + f ( n − 2 ) f(n) = f(n-1) + f(n-2) f(n)=f(n−1)+f(n−2)
我们可以得到这样一个关系:
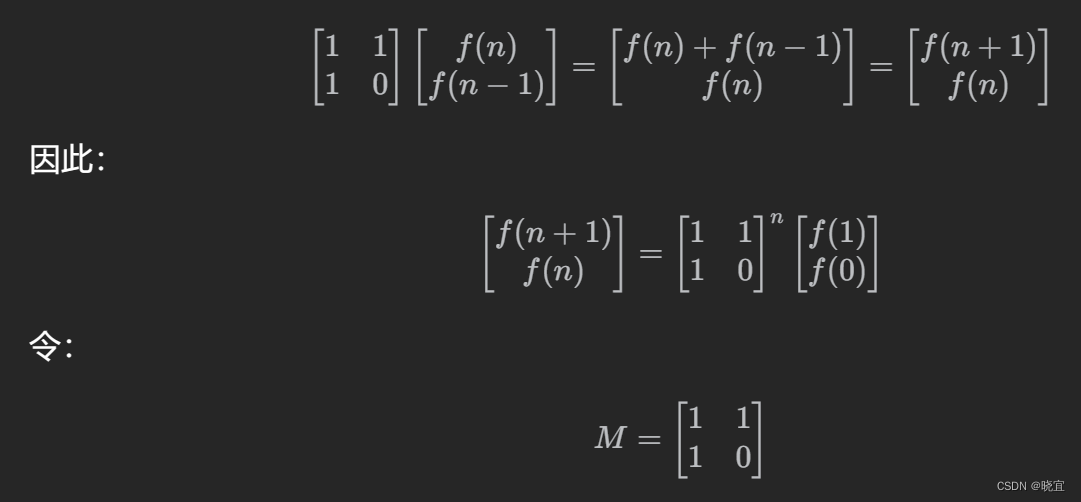
只要我们快速的求出矩阵的n次幂,那么我们就可以得出f(n),即最终答案。这里快速求解矩阵的方法,正是刚刚所讲的快速幂解法。
Code
class Solution {public int climbStairs(int n) {int[][] q = {{1,1},{1,0}};int[][] res = pow(q,n);return res[0][0];}public int[][] pow(int[][] a,int n){int[][] ret = {{1,0},{0,1}};while(n>0){if( (n&1)==1 ){ret = multiply(ret,a);}n >>= 1;a = multiply(a,a);}return ret;}public int[][] multiply(int[][] a,int[][] b){int[][] c = new int[2][2];for(int i=0;i<2;i++){for(int j=0;j<2;j++){c[i][j] = a[i][0] * b[0][j] + a[i][1] * b[1][j];}}return c;}}
复杂度
时间复杂度:
只需要求 l o g ( n ) log(n) log(n)次, O ( l o g n ) O(logn) O(logn)
空间复杂度:
O ( 1 ) O(1) O(1)
