第十届蓝桥杯大赛个人赛省赛(软件类) CC++ 研究生组2.0
A立方和
#include<iostream>
#include<cmath>
using namespace std;
int main(){int n, t, flag, x;long long ans = 0;for(int i = 1; i <= 2019; i++){t = i;flag = 0;while(t && !flag){x = t % 10;if(x == 2 || x == 0 || x == 1 || x == 9) flag = 1;t /= 10;}if(flag) ans += (long long)pow(i, 3);}printf("%lld", ans);//4097482414389return 0;
}
打卡题
B字串数字
#include<iostream>
#include<string>
using namespace std;
int main(){string s = "LANQIAO";
// string s = "LQ";long long power = 1, ans = 0;for(int i = s.size() - 1; i >= 0; i--){ans += (s[i] - 'A' + 1) * power;power *= 26;}printf("%lld", ans);//3725573269return 0;
}
进制转换
C质数
#include<iostream>
#include<cmath>
using namespace std;
typedef long long ll;
bool isPrime(ll n){ll sqr = sqrt(n);for(int i = 2; i <= sqr; i++){if(n % i == 0) return false;}return true;
}
int main(){ll x = 2, cnt = 0, ans;while(cnt < 2019){if(isPrime(x)){cnt++;ans = x;}x++;}printf("%lld", ans);//17569return 0;
}
类似于质数打表
D最短路
6
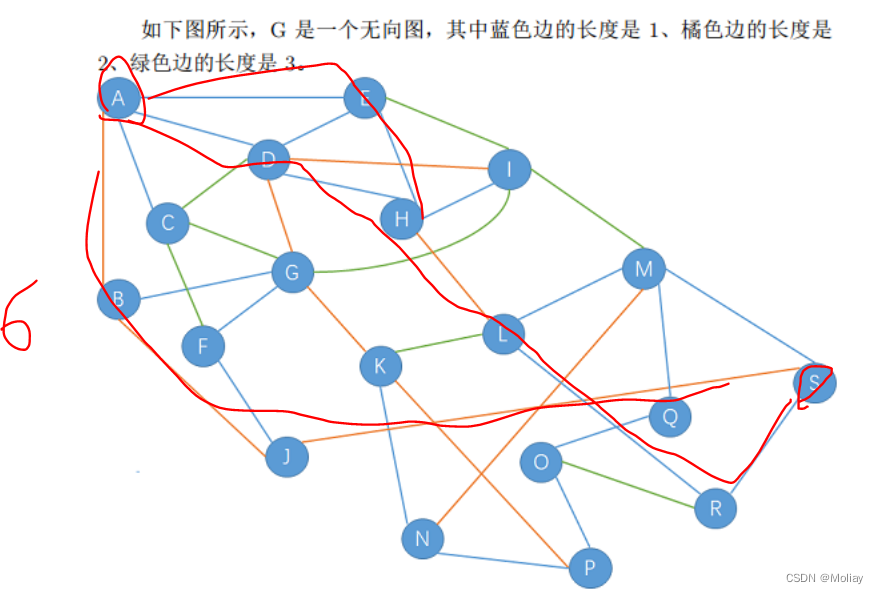
适当手算,灵活些
E RSA解密
没思路
尝试先把p,q试出来
#include<iostream>
#include<cmath>
using namespace std;
typedef long long ll;
int main(){ll n = 1001733993063167141LL, sqr = sqrt(n);for(ll i = 2; i <= sqr; i++){if(n % i == 0){printf("%lld ", i);if(i * i != n) printf("%lld ", n / i);}}return 0;
}
发现de % (p-1)(q-1)=1其实也就是求d的逆元,联想到用扩欧。
解密过程是快速幂的经典应用啦~
#include<iostream>
#include<cmath>
using namespace std;
typedef __int128 ll;ll exGcd(ll a, ll b, ll &x, ll &y){if(b == 0){x = 1;y = 0;return a;}int g = exGcd(b, a % b, x, y), temp = x;x = y;y = temp - a / b * y;return g;
}ll inverse(ll a, ll b){ll x, y;ll g = exGcd(a, b, x, y);if(g == 1) return (x % b + b) % b;else return -1;
}ll fastPow(ll a, ll b, ll m){//计算过程中会有超出long long的情况,故设置为__int128类型 if(b == 0) return 1;else if(b & 1) return a * fastPow(a, b - 1, m) % m;else{ll t = fastPow(a, b / 2, m);return t * t % m;}
}int main(){ll p = 891234941LL, q = 1123984201LL, d = 212353, n = 1001733993063167141LL, e, c = 20190324LL;ll t = (p - 1) * (q - 1);e = inverse(d, t);//de % t = 1 扩欧求d的逆元 printf("%lld", fastPow(c, e, n));//快速幂return 0;
}
F 斐波那契额序列与黄金分割
先打印前一百个观察下数据,发现大于等于19后在保留八位小数的基础上就稳定在一个比值,符合提示的趋近于黄金分割。而且当数值过大时,比值会出现负数的情况,显然异常。考虑可能是因为斐波那契额数列增长速度过快,超出了int型范围。才100就超了,给定的n范围更超,索性利用后续在规定的精度内稳定于一个比值,直接打印不再计算。
#include<iostream>
using namespace std;
typedef long long ll;
int main(){ll f1 = 1, f2 = 1, f, n;for(int i = 3; i <= 100; i++){f = f1 + f2;printf("%d %.8f\n", i - 1, 1.0 * f2 / f);f1 = f2;f2 = f;}return 0;
}
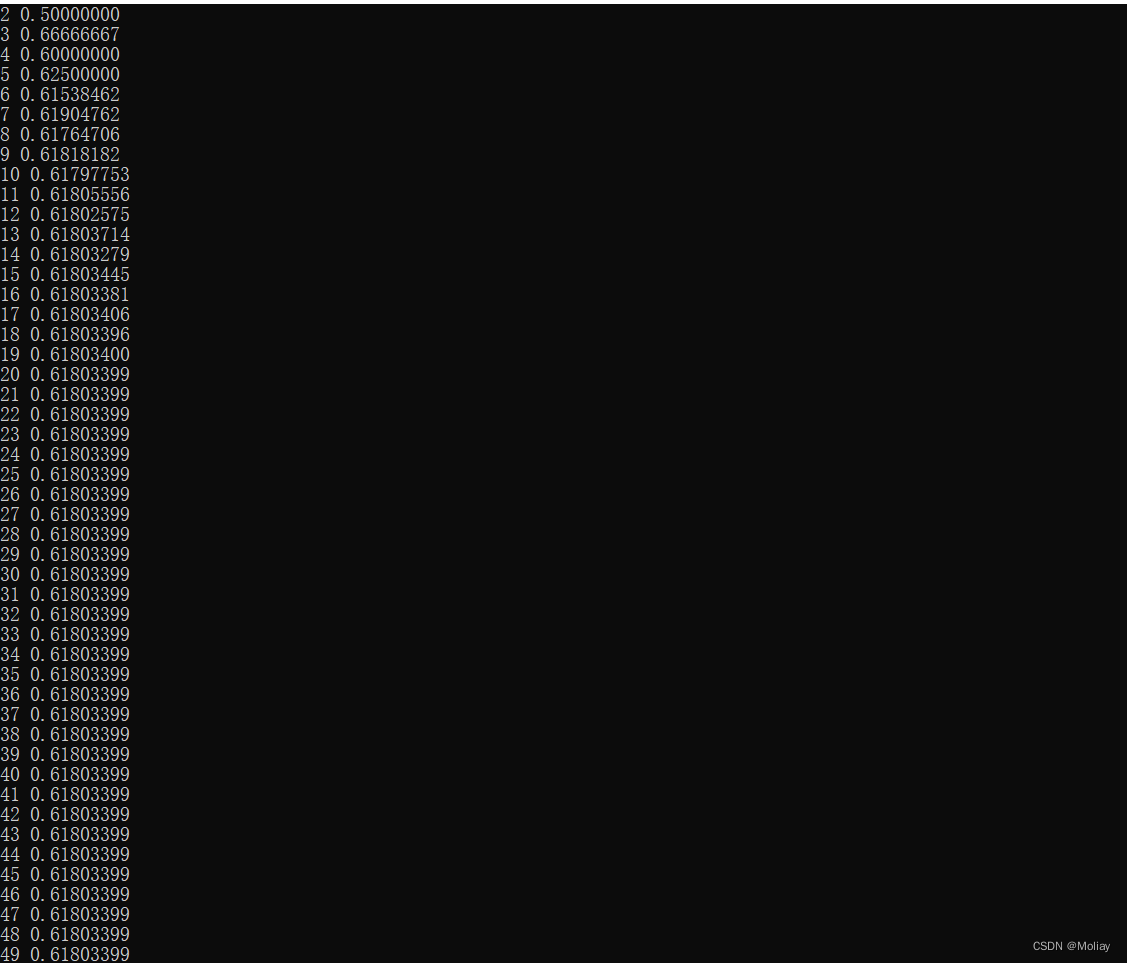
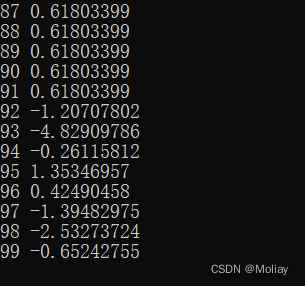
提交程序为
#include<iostream>
using namespace std;
typedef long long ll;
int main(){ll f1 = 1, f2 = 1, f, n;scanf("%lld", &n);if(n > 20) printf("0.61803399");else{for(int i = 3; i <= n + 1; i++){f = f1 + f2;if(i == n + 1)printf("%.8f", 1.0 * f2 / f);f1 = f2;f2 = f;}}return 0;
}
一个测试点没过,忽略了n==2的情况
#include<iostream>
using namespace std;
typedef long long ll;
int main(){ll f1 = 1, f2 = 1, f, n;scanf("%lld", &n);if(n > 20) printf("0.61803399");else{for(int i = 2; i < n + 1; i++){f = f1 + f2;f1 = f2;f2 = f;}printf("%.8f", 1.0 * f1 / f2);}return 0;
}
G扫地机器人
不知道如何下手
走廊长度n为105,根据数据范围需要选择nlogn以内的算法。花费时间最短2,最长2*n,考虑二分处理。
在花费时间t内,判断是否能够扫完n个格子。用贪心,尽量让机器人扫其周围的格子且平均得划分。把机器人的位置升序排序,看机器人在时间t内,能够覆盖的右边界能否相互衔接上且最后一个机器人能够覆盖到走廊有边界。
#include<iostream>
#include<algorithm>
using namespace std;
const int maxn = 1e5 + 10;
int a[maxn], n, k, l, r, mid;bool judge(int len){int r = 0;//上一个机器人能扫到的右边界for(int i = 0; i < k; i++){if(a[i] - len > r) return false;//不能衔接上,有覆盖不到的区域,则不可行else{if(a[i] < r) r = a[i] + len - 1;//在上一个机器人可覆盖的区域内else r += len;//在边界上 } }return r >= n;
}int main(){scanf("%d%d", &n, &k);for(int i = 0; i < k; i++){scanf("%d", a + i);}sort(a, a + k);l = 0;r = n;while(l < r){mid = (l + r) / 2;if(judge(mid)) r = mid;//当前可行,尝试更短 else l = mid + 1; //当前不可行,增加时间 }printf("%d", 2 * (l - 1)); return 0;
}
H修改数组
#include<iostream>
using namespace std;
const int maxn = 1e5 + 10, maxv = 1e6 + 1e5;
int a[maxn], flag[maxv] = {0};
int main(){int n;scanf("%d", &n);for(int i = 0; i < n; i++){scanf("%d", a + i);if(!flag[a[i]]) flag[a[i]] = 1;else {a[i] += flag[a[i]];while(flag[a[i]]) a[i]++;flag[a[i]]++;}}for(int i = 0; i < n; i++){printf("%d ", a[i]);}return 0;
}
两个测试点超时
没有充分利用flag的出现次数,还是一个个的跳且没有正确累加后续的出现次数
#include<iostream>
using namespace std;
const int maxn = 1e5 + 10, maxv = 1e6 + 1e5;
int a[maxn], flag[maxv] = {0};
int main(){int n, t;scanf("%d", &n);for(int i = 0; i < n; i++){scanf("%d", a + i);while(flag[a[i]]){t = a[i];a[i] += flag[t];flag[t]++;}flag[a[i]] = 1;}for(int i = 0; i < n; i++){printf("%d ", a[i]);}return 0;
}
I 灵能传输
#include<iostream>
#include<algorithm>
using namespace std;
const int maxn = 3e5 + 10;
int a[maxn];
int main(){int t, n, flag, x, p, temp;scanf("%d", &t);while(t--){scanf("%d", &n);for(int i = 0; i < n; i++){scanf("%d", a + i);}flag = 1;while(flag){x = abs(a[0]);p = 0;for(int i = 1; i < n; i++){if(abs(a[i]) > x){x = abs(a[i]);p = i;}}if(x == 0) flag = 1;if(p == 0) p++;else if(p == n - 1) p--;temp = max(max(abs(a[p - 1] + a[p]), abs(a[p + 1] + a[p])), abs(a[p]));if(temp >= x) flag = 0;else{a[p - 1] += a[p];a[p + 1] += a[p];a[p] = -a[p];}}printf("%d\n", x);}return 0;
}
骗了四个测试点的分。
#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
typedef long long ll;
int main(){int n, t;scanf("%d", &t);while(t--){ll x, ansX = 0;scanf("%d", &n);vector<ll> sum(n + 1, 0);vector<ll> visit(n + 1, 0);vector<ll> ans(n + 1, 0); for(int i = 1; i <= n; i++){scanf("%lld", &x);sum[i] = sum[i - 1] + x;}ll l = sum[0], r = sum[n], lp = 0, rp = n, ansL = 0, ansR = n;//首位项的值if(l > r) swap(l, r);sort(sum.begin(), sum.end());for(int i = 0; i < n; i++){if(sum[i] == l){lp = i;break;}}for(int i = 0; i < n; i++){if(sum[i] == r){rp = i;break;}}for(int i = rp; i <= n; i += 2){//填充结果数组 ans[ansR--] = sum[i];visit[i] = 1; }for(int i = lp; i >= 0; i -= 2){ans[ansL++] = sum[i];visit[i] = 1;}for(int i = 0; i <= n; i++){if(!visit[i]) ans[ansL++] = sum[i];}for(int i = 1; i <= n; i++){if(abs(ans[i] - ans[i - 1]) > ansX) ansX = abs(ans[i] - ans[i - 1]);}printf("%lld\n", ansX);}return 0;
}
J空间跳跃
题干看起来好麻烦,蒟蒻不想做了
