PCA(Principal Component Analysis,主成分分析)
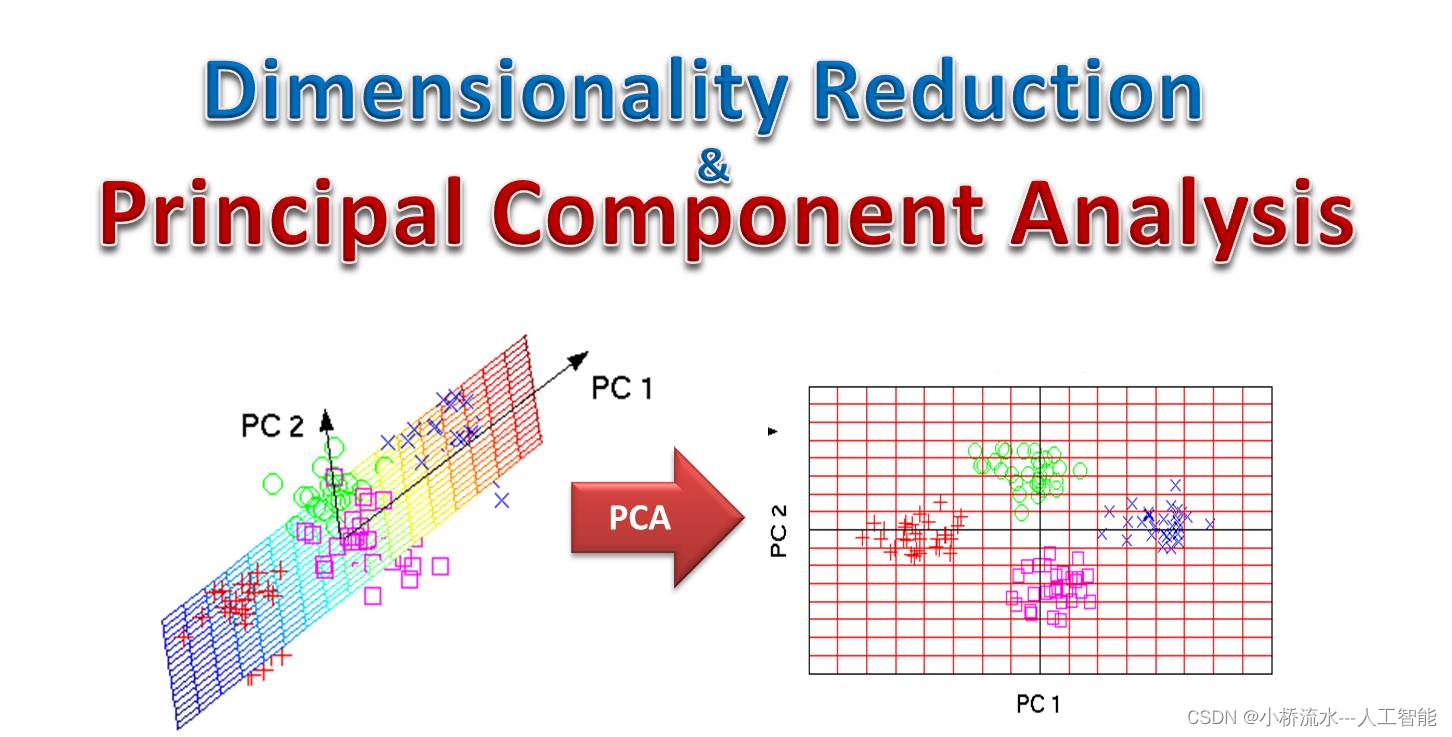
PCA(Principal Component Analysis,主成分分析)是一种在数据分析中广泛应用的统计方法,主要用于数据降维、可视化和去噪。以下是对PCA的发展史、工作原理以及理论基础的详细解释:
Principal Component Analysis
- 一、PCA的发展史
- 二、PCA的工作原理
- 三、PCA的理论基础
- 总结
一、PCA的发展史
PCA方法的历史可以追溯到较早的统计学和数学领域。然而,其作为主成分分析的概念和术语的明确提出,则是在20世纪初。随着计算机技术的发展,PCA在数据处理和分析中的应用越来越广泛。特别是在现代数据分析中,PCA已经成为一种标准的工具,用于从高维数据中提取关键信息,降低数据的复杂性,同时保留其最重要的特征。
二、PCA的工作原理
PCA的工作原理的核心目标是将原始的高维数据映射到一个低维空间,同时尽可能保留数据中的关键信息。具体步骤如下:
- 计算协方差矩阵:首先,PCA会计算数据集中各变量之间的协方差矩阵。这个矩阵包含了变量之间的线性相关性信息。
- 特征值分解:接着,PCA会对协方差矩阵进行特征值分解。这个过程会找到协方差矩阵的特征向量和特征值。特征向量代表了数据的主要变化方向,而特征值则衡量了这些方向上数据变化的程度。
- 选择主成分:根据特征值的大小,PCA会选择前几个最大的特征值对应的特征向量作为主成分。这些主成分代表了数据中的主要变化模式,且彼此之间是正交的(即不相关)。
- 数据转换:最后,PCA会将原始数据转换到由这些主成分构成的新坐标系中。这个过程相当于将数据投影到低维空间,实现了数据的降维。
三、PCA的理论基础
PCA的理论基础主要建立在线性代数和统计学之上。以下是几个关键概念:
- 基变换:PCA通过基变换将原始数据从高维空间映射到低维空间。这种变换是通过选择新的基向量(即主成分)来实现的,这些基向量能够最好地表示原始数据的主要特征。
- 协方差和散度矩阵:协方差矩阵衡量了变量之间的线性相关性,而散度矩阵则描述了数据的分布情况。PCA通过计算这些矩阵来找到数据的主要变化方向和程度。
- 特征值分解和SVD分解:这两种数学工具都是PCA实现数据降维的关键。特征值分解用于找到协方差矩阵的特征向量和特征值,而SVD(奇异值分解)则是一种更一般的矩阵分解方法,也可以用于PCA的计算。
- 信息保留:PCA的目标是在降维的同时尽可能保留原始数据中的信息。这通过选择最大的特征值对应的特征向量作为主成分来实现,因为这些方向上的数据变化最大,包含了最多的信息。
总结
总的来说,PCA是一种强大的数据分析工具,它通过降维技术将高维数据转化为低维表示,同时保留数据的主要特征。其工作原理基于线性代数和统计学的理论基础,通过计算协方差矩阵、特征值分解等步骤实现数据的降维和信息的提取。
