多叉树题目:N 叉树的层序遍历
文章目录
- 题目
- 标题和出处
- 难度
- 题目描述
- 要求
- 示例
- 数据范围
- 解法
- 思路和算法
- 代码
- 复杂度分析
题目
标题和出处
标题:N 叉树的层序遍历
出处:429. N 叉树的层序遍历
难度
4 级
题目描述
要求
给定一个 N 叉树的根结点 root \texttt{root} root,返回其结点值的层序遍历。
N 叉树在输入中按层序遍历序列化表示,每组子结点由空值 null \texttt{null} null 分隔(请参见示例)。
示例
示例 1:
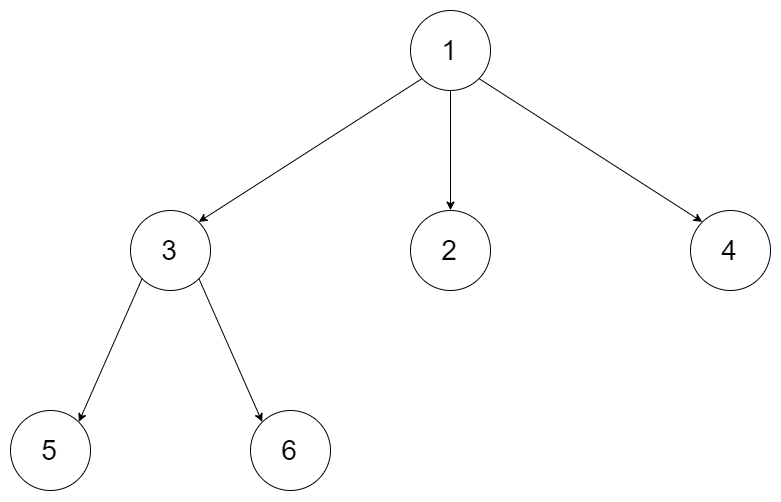
输入: root = [1,null,3,2,4,null,5,6] \texttt{root = [1,null,3,2,4,null,5,6]} root = [1,null,3,2,4,null,5,6]
输出: [[1],[3,2,4],[5,6]] \texttt{[[1],[3,2,4],[5,6]]} [[1],[3,2,4],[5,6]]
示例 2:
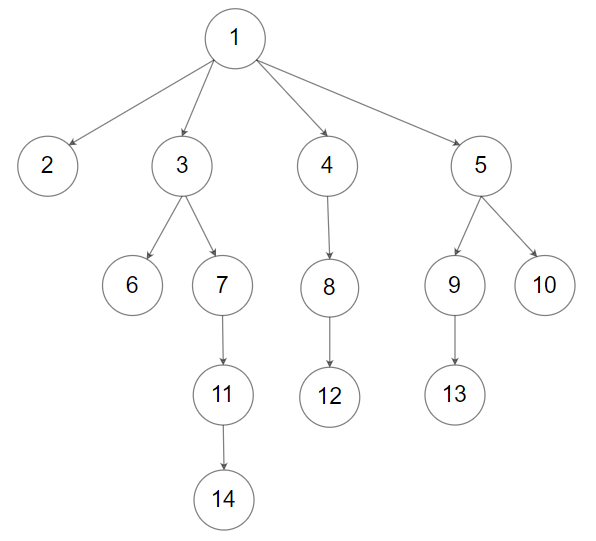
输入: root = [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14] \texttt{root = [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14]} root = [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14]
输出: [[1],[2,3,4,5],[6,7,8,9,10],[11,12,13],[14]] \texttt{[[1],[2,3,4,5],[6,7,8,9,10],[11,12,13],[14]]} [[1],[2,3,4,5],[6,7,8,9,10],[11,12,13],[14]]
数据范围
- 树中结点数目在范围 [0, 10 4 ] \texttt{[0, 10}^\texttt{4}\texttt{]} [0, 104] 内
- N 叉树的高度小于或等于 1000 \texttt{1000} 1000
解法
思路和算法
层序遍历的方法为从根结点开始依次遍历每一层的结点,由于每一层与根结点的距离依次递增,因此可以使用广度优先搜索实现层序遍历。
广度优先搜索需要使用队列存储待访问的结点,初始时将根结点入队列。每次将一个结点出队列,然后将该结点的子结点入队列,直到队列为空时遍历结束。
由于这道题需要将结点值按照不同层分组,因此需要区分不同结点所在的层,确保每一轮访问的结点为同一层的全部结点。
初始时,队列内只有根结点,是同一层的全部结点。每一轮访问结点之前需要首先得到队列内的元素个数,此时队列内的元素为同一层的全部结点,然后访问这些结点,并将这些结点的子结点入队列。一轮访问结束之后,当前层的全部结点都已经出队列并被访问,此时队列内的元素为下一层的全部结点,下一轮访问时即可访问下一层的全部结点。使用上述做法,可以确保每一轮访问的结点为同一层的全部结点。
对于每一层维护一个结点值序列。遍历完每一层结点之后,将该层结点值序列添加到层序遍历序列中。
代码
class Solution {public List<List<Integer>> levelOrder(Node root) {List<List<Integer>> levelOrderTraversal = new ArrayList<List<Integer>>();if (root == null) {return levelOrderTraversal;}Queue<Node> queue = new ArrayDeque<Node>();queue.offer(root);while (!queue.isEmpty()) {List<Integer> levelValues = new ArrayList<Integer>();int size = queue.size();for (int i = 0; i < size; i++) {Node node = queue.poll();List<Node> children = node.children;levelValues.add(node.val);for (Node child : children) {queue.offer(child);}}levelOrderTraversal.add(levelValues);}return levelOrderTraversal;}
}
复杂度分析
-
时间复杂度: O ( m ) O(m) O(m),其中 m m m 是二叉树的结点数。每个结点都被访问一次。
-
空间复杂度: O ( m ) O(m) O(m),其中 m m m 是二叉树的结点数。空间复杂度主要是队列空间,队列内元素个数不超过 m m m。
