【4】单链表(有虚拟头节点)
【4】单链表(有虚拟头节点)
- 1、虚拟头节点
- 2、构造方法
- 3、node(int index) 返回索引位置的节点
- 4、添加
- 5、删除
- 6、ArrayList 复杂度分析
- (1) 复杂度分析
- (2) 数组的随机访问
- (3) 动态数组 add(E element) 复杂度分析
- (4) 动态数组的缩容
- (5) 复杂度震荡
- 7、单链表复杂度分析
- 8、完整代码
1、虚拟头节点
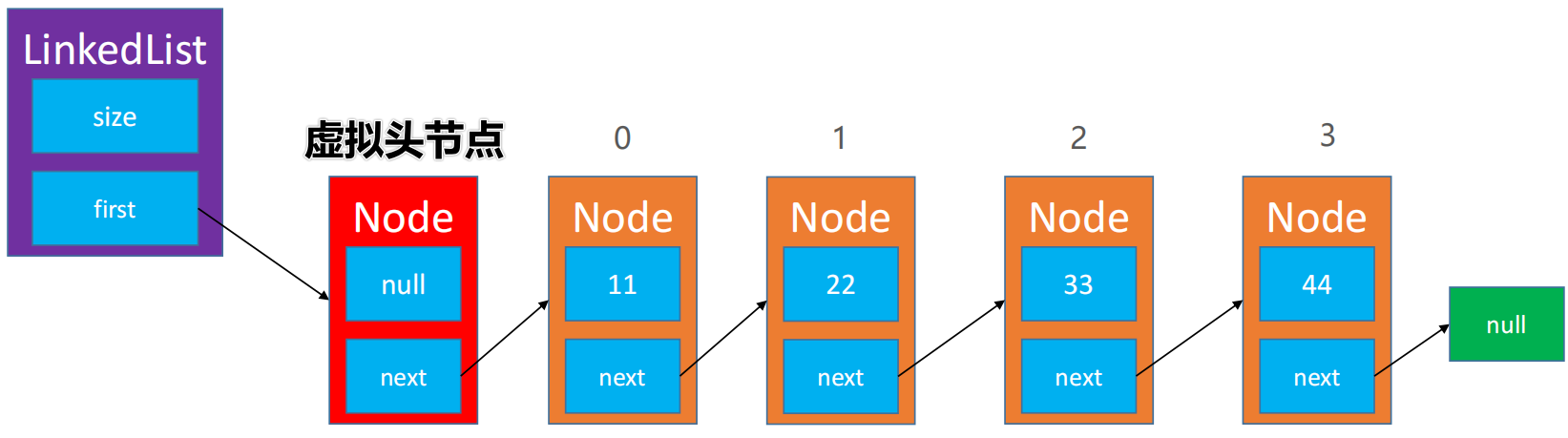
📕 为了让代码更精简,统一所有节点的处理逻辑,可以在最前面增加一个虚拟头节点
🖊 头指针指向的永远是虚拟头节点
🖊 虚拟头节点不存储数据
2、构造方法
📕 在 单链表 代码的基础上需要进行修改
🖊 头指针 first 永远指向虚拟头节点,所以在 VirtualHeadLinkedList 的构造方法中要让 first 指针虚拟头节点
public VirtualHeadLinkedList() {// 头指针指向虚拟头节点// 虚拟头节点的next默认指向nullfirst = new Node<>(null, null);}
3、node(int index) 返回索引位置的节点
🖊 该方法会返回索引位置的节点,它原本的实现思路是:若需要
index位置的节点,则从first头指针指向的头节点开始 next index 次🖊 加入了虚拟头节点后,就不能从
first头指针指向的头节点开始 next index 次了,而是从虚拟头节点的 next 指向的节点开始next
/*** 返回index索引处的节点*/private Node<E> node(int index) {checkIndex(index);// first头指针指向的是虚拟头节点// first.next就是具体存储数据的第一个节点Node<E> node = first.next;for (int i = 0; i < index; i++) {node = node.next;}return node;}
4、添加
🖊 之前的添加逻辑:
① 假如是往头节点位置添加元素:first指向新节点,新节点的 next 指向之前的头节点
② 若不是往头节点位置添加元素:找到index-1索引处的节点prev,然后新节点的 next 指向prev.next,然后prev.next指向新节点
🖊 增加虚拟头节点后: 如果
index == 0,prev 就是虚拟头节点(first)
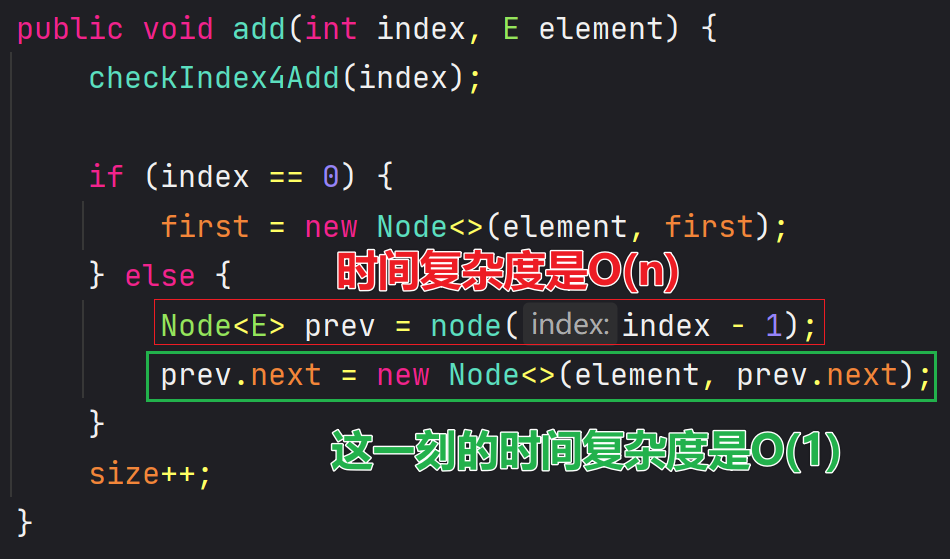
/*** 往索引位置添加元素*/@Overridepublic void add(int index, E element) {checkIndex4Add(index);// 如果index==0, prev是虚拟头节点Node<E> prev = (index == 0) ? first : node(index - 1);prev.next = new Node<>(element, prev.next);size++;}
5、删除
🖊 假如删除的是
index == 0位置的节点,则prev就是虚拟头节点
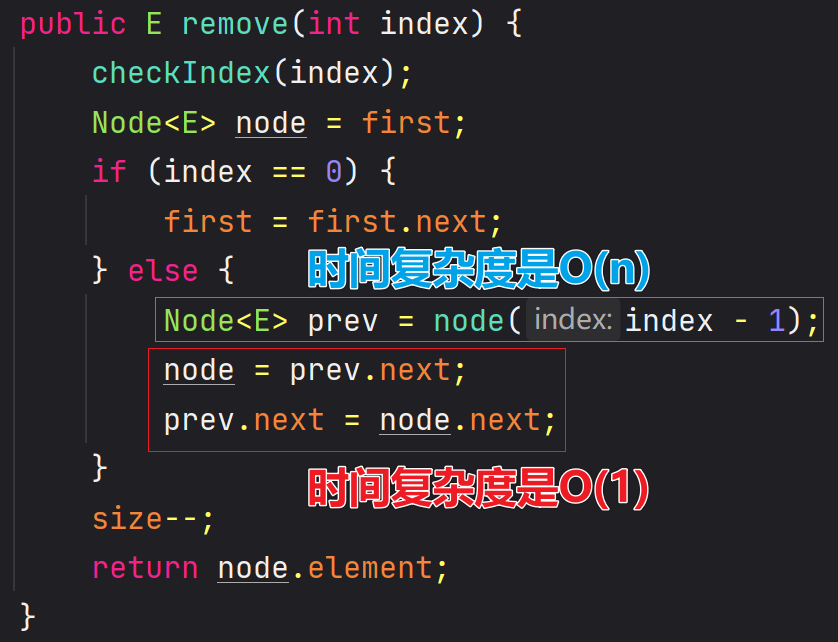
/*** 删除索引位置的元素** @return 被删除的元素*/@Overridepublic E remove(int index) {checkIndex(index);Node<E> prev = (index == 0) ? first : node(index - 1);Node<E> node = prev.next;prev.next = node.next;size--;return node.element;}
6、ArrayList 复杂度分析
(1) 复杂度分析
◼ 最好情况复杂度
◼ 最坏情况复杂度
◼ 平均情况复杂度
| 方法 | 复杂度 |
|---|---|
get | O(1) |
set | O(1) |
add | ① 最好:O(1) ② 最坏:O(n) ③ 平均:O(n) |
remove | ① 最好:O(1) ② 最坏:O(n) ③ 平均:O(n) |
📕
add:
🖊 假如index == size(往最后面添加元素):无需挪动元素(时间复杂度是O(1))最好时间复杂度
🖊 假如index == 0:整个数组需要往后挪动(时间复杂度是O(n))最坏时间复杂度
🖊 平均时间复杂度:(1 + 2 + ... + n) / n = n/2【挪动1次、2次、...、 n次】
(2) 数组的随机访问
🖊 数组的随机访问速度非常快
🖊elements[n]的效率与 n 是多少无关
📕 假设存放的是 int 类型的元素(每个元素的地址相差四个字节):
🖊 地址值 = index * 4 + 数组首元素的地址
(3) 动态数组 add(E element) 复杂度分析
◼ 最好:O(1)
◼ 最坏:O(n)
◼ 平均:O(1)
◼ 均摊:O(1)
🖊
add(E element)永远是往数组的最后面添加元素,可能会有扩容的情况产生
🖊 扩容的时间复杂度是O(n)
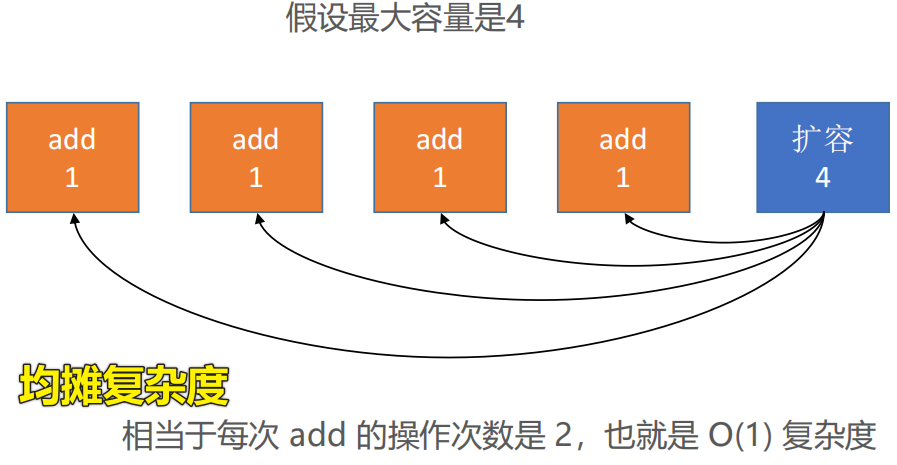
🖊 但是该方法大部分情况下的时间复杂度都是O(1),只有极少数情况是O(n)【均摊复杂度】
📕 什么情况下适合使用均摊复杂度❓
🖊经过连续的多次复杂度比较低的情况后,出现个别复杂度比较高的情况
(4) 动态数组的缩容
📕 如果内存使用比较紧张,动态数组有比较多的剩余空间,可以考虑进行缩容操作
🖊 比如剩余空间占总容量的一半时,就进行缩容
/*** 缩容*/private void trim() {// 当前容量:elements数组最多可以存储的元素个数int curCap = elements.length;int newCap = curCap >> 1;if (size >= newCap || newCap <= DEFAULT_CAPACITY) return; // 不缩容E[] newElements = (E[]) new Object[newCap];// 把旧数组元素复制到新数组中for (int i = 0; i < size; i++) {newElements[i] = elements[i];}elements = newElements;System.out.println("🖊缩容:" + curCap + "→" + newCap);}
(5) 复杂度震荡
📕 如果扩容倍数、缩容时机设计不得当,有可能会导致复杂度震荡
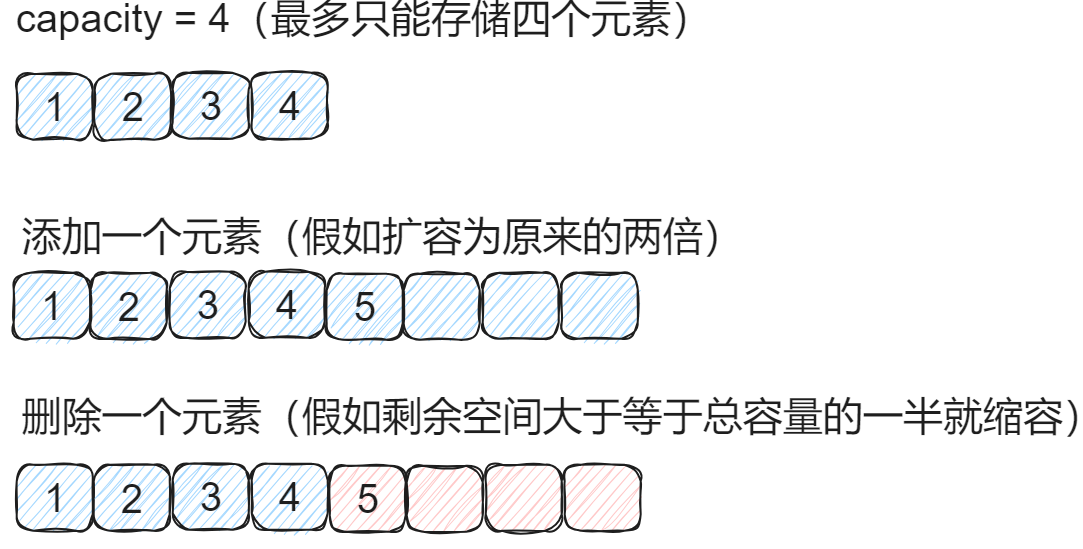
🖊 上图假如一直执行增、删、增、删、增、删…操作的话,就会出现扩容、缩容、扩容、缩容、扩容、缩容…的情况
🖊 出现此情况是因为:扩容为2倍(2)和剩余空间大于等于总容量一半(1/2)的时候缩容【扩容倍数和缩容时机的乘积不要等于1】
7、单链表复杂度分析
| 方法 | 复杂度 |
|---|---|
get | ① 最好:O(1) ② 最坏:O(n) ③ 平均:O(n) |
set | ① 最好:O(1) ② 最坏:O(n) ③ 平均:O(n) |
add | ① 最好:O(1) ② 最坏:O(n) ③ 平均:O(n) |
remove | ① 最好:O(1) ② 最坏:O(n) ③ 平均:O(n) |
🖊 单链表效率比较低主要是因为
node(int index)方法,它有 for 循环(数据规模可能是 n)
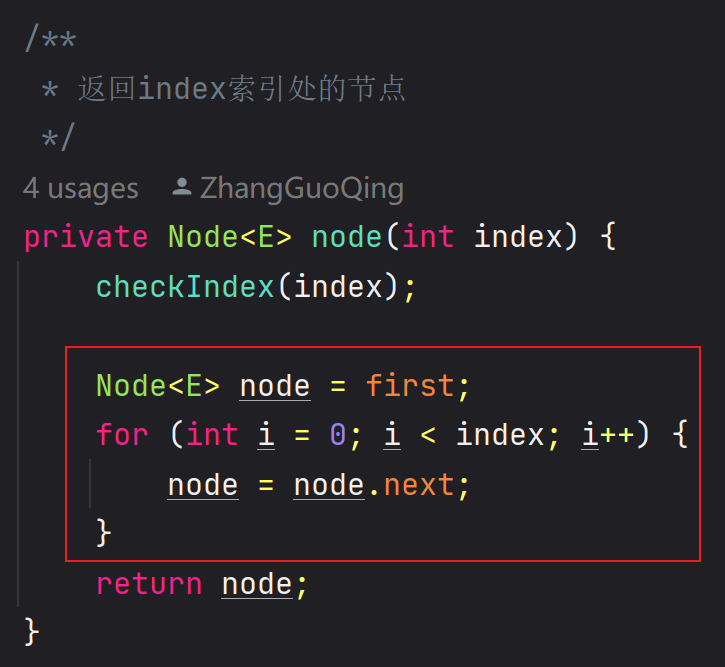
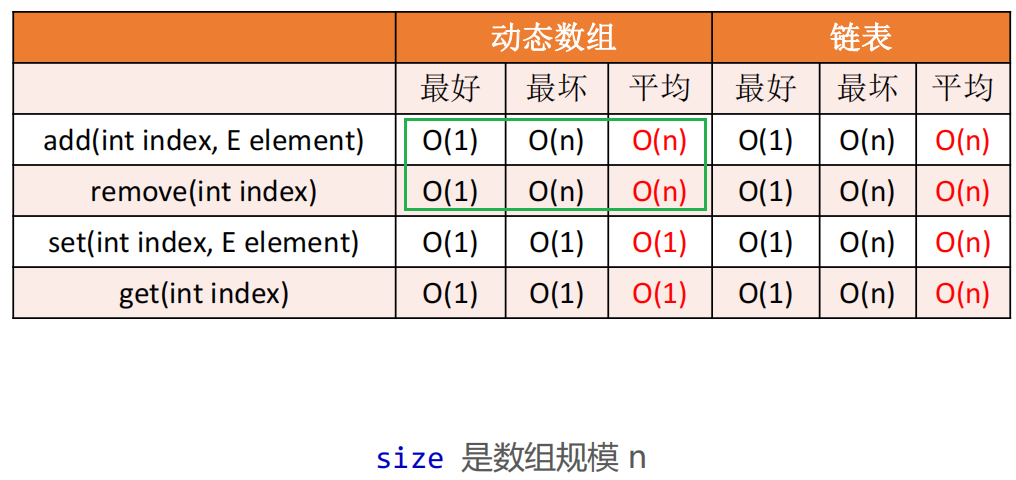
🖊 有的资料说链表添加和删除的复杂度是O(1),这说的是添加和删除的 “哪一刻”,但找到 prev 的时间复杂度可能是 O(n)
8、完整代码
🖊 带有虚拟头节点的单链表完整代码