【算法刷题 | 二叉树 04】3.27(翻转二叉树、对称二叉树、完全二叉树的节点个数、平衡二叉树、完全二叉树的所有路径)
文章目录
- 6.翻转二叉树
- 6.1问题
- 6.2解法一:递归
- 6.2.1递归思路
- (1)确定递归函数的参数和返回值
- (2)确定终止条件
- (3)确定单层递归的逻辑
- 6.2.2全部代码
- 6.3解法二:层序遍历
- 7.对称二叉树
- 7.1问题
- 7.2解法一:递归
- 7.2.1递归思路
- (1)确定递归函数的参数和返回值
- (2)确定终止条件
- (3)确定单层递归的逻辑
- 7.2.2代码实现
- 7.3解法二:迭代法
- 8.完全二叉树的节点个数
- 8.1问题
- 8.2解法一:递归
- 8.3解法二:层序遍历
- 9.平衡二叉树
- 9.1问题
- 9.2解法一:递归
- 9.2.1递归思路
- (1)确定递归函数返回值和参数值
- (2)确定终止条件
- (3)确定递归逻辑
- 9.2.2代码
- 10.完全二叉树的所有路径
- 10.1问题
- 10.2解法一:前序遍历+回溯
- 10.2.1递归思路
- (1)确定递归函数参数以及返回值
- (2)确定递归终止条件
- (3)确定递归逻辑
- 10.2.2代码实现
6.翻转二叉树
6.1问题
给你一棵二叉树的根节点 root ,翻转这棵二叉树,并返回其根节点。
- 示例一:
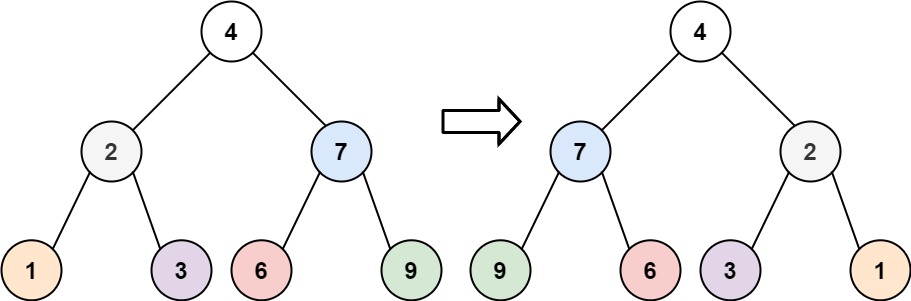
输入:root = [4,2,7,1,3,6,9]
输出:[4,7,2,9,6,3,1]
6.2解法一:递归
6.2.1递归思路
(1)确定递归函数的参数和返回值
- 题目为翻转根节点的左右孩子
- 最后返回根节点,即每次递归,传入TreeNode节点,返回该节点
TreeNode reverse(TreeNode node);
(2)确定终止条件
- 当递归到的该节点为空,即返回
if(node==null){return;
}
(3)确定单层递归的逻辑
- 当确定该节点不为空,先交换左、右孩子
- 再分别递归左孩子、右孩子
swap(node);
reverse(node.left);
reverse(node.right);
6.2.2全部代码
class Solution {public TreeNode invertTree(TreeNode root) {if(root==null){return root;}return reverse(root);}private TreeNode reverse(TreeNode node){if(node==null){return node;}swap(node);reverse(node.left);reverse(node.right);return node;}private void swap(TreeNode node){TreeNode tmp=node.left;node.left=node.right;node.right=tmp;}
}
6.3解法二:层序遍历
- 将每一个从队列取出来的元素,进行左孩子和有孩子的交换
class Solution {public TreeNode invertTree(TreeNode root) {//广度优先遍历Queue<TreeNode> queue=new LinkedList<>();if(root==null){return root;}queue.offer(root);while(!queue.isEmpty()){int size=queue.size();while(size>0){TreeNode node=queue.poll();swap(node);if(node.left!=null){queue.offer(node.left);}if(node.right!=null){queue.offer(node.right);}size--;}}return root;}private void swap(TreeNode node){TreeNode tmp=node.left;node.left=node.right;node.right=tmp;}
}
7.对称二叉树
7.1问题
给你一个二叉树的根节点 root , 检查它是否轴对称。
- 示例一:
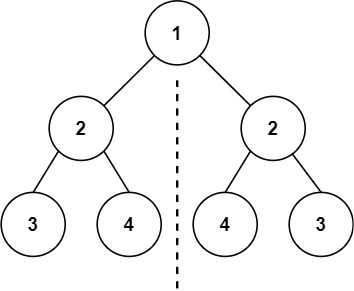
输入:root = [1,2,2,3,4,4,3]
输出:true
7.2解法一:递归
7.2.1递归思路
(1)确定递归函数的参数和返回值
- 比较的是根节点的两个子树是否是相互翻转的,进而判断这个树是不是对称树,所以要比较的是两个树,参数自然也是左子树节点和右子树节点。
- 返回值为boolean类型
boolean compare(TreeNode left,TreeNode right)
(2)确定终止条件
- 首先排除左孩子、右孩子节点有空的情况
- 左孩子为空,右孩子不为空:return false
- 左孩子不为空,右孩子为空:return false
- 左、右孩子均为空:return true
- 左、右孩子均不为空:
- 比较左右孩子的数值,不相同:return false
if (left == NULL && right != NULL) return false;
else if (left != NULL && right == NULL) return false;
else if (left == NULL && right == NULL) return true;
else if (left->val != right->val) return false; // 注意这里我没有使用else
(3)确定单层递归的逻辑
- 单层递归的逻辑就是处理左右节点都不为空,且数值相同的情况。
- 比较二叉树外侧是否对称:传入的是左节点的左孩子,右节点的右孩子。
- 比较内侧是否对称,传入左节点的右孩子,右节点的左孩子。
- 如果左右都对称就返回true ,有一侧不对称就返回false 。
boolean outside = compare(left.left, right.right); // 左子树:左、 右子树:右
boolean inside = compare(left.right, right.left); // 左子树:右、 右子树:左
boolean isSame = outside && inside; // 左子树:中、 右子树:中(逻辑处理)
return isSame;
7.2.2代码实现
class Solution {public boolean isSymmetric(TreeNode root) {if(root==null){return true;}return compare(root.left,root.right);}private boolean compare(TreeNode left,TreeNode right){if(left==null && right!=null){return false;}else if(left!=null && right==null){return false;}else if(left==null && right==null){return true;}else if(left.val!=right.val){return false;}//单层递归逻辑boolean out=compare(left.left,right.right);boolean in=compare(left.right,right.left);return (out&&in);}
}
7.3解法二:迭代法
- 使用队列来比较两个树(根节点的左右子树)是否相互翻转,(注意这不是层序遍历)
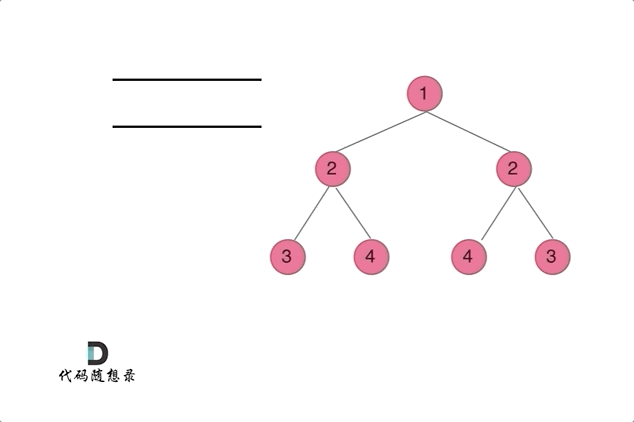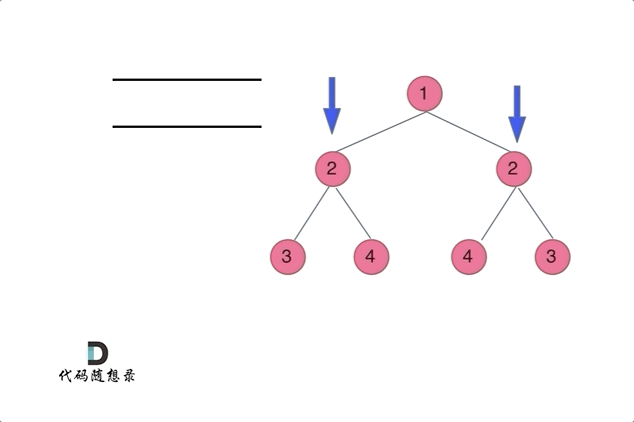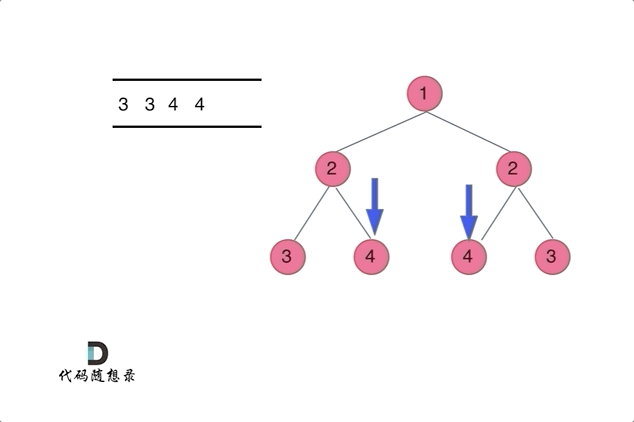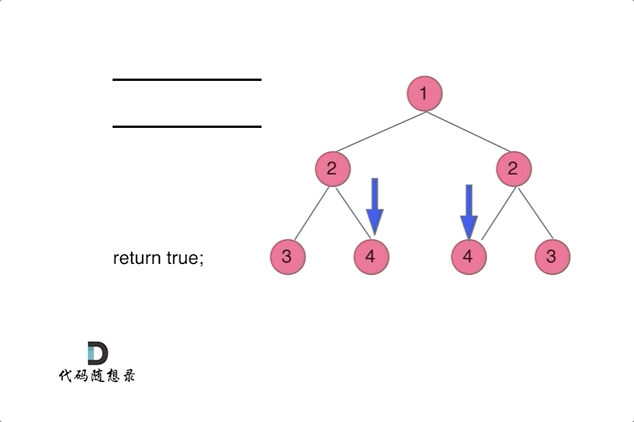
class Solution {public boolean isSymmetric(TreeNode root) {//迭代法if(root==null){return true;}Queue<TreeNode> queue=new LinkedList<>();//添加根节点的左右孩子queue.offer(root.left);queue.offer(root.right);while(!queue.isEmpty()){TreeNode left=queue.poll();TreeNode right=queue.poll();//1、判断两个节点是否均为空if(left==null && right==null){continue; //对称,结束此次循环,再次取出新的两个节点判断}//2、判断不符合对称条件if(left==null || right==null || (left.val!=right.val)){return false;}//3、添加新的两个节点:外层+内层queue.offer(left.left);queue.offer(right.right);queue.offer(left.right);queue.offer(right.left);}return true;}}
8.完全二叉树的节点个数
8.1问题
给你一棵 完全二叉树 的根节点 root ,求出该树的节点个数。
完全二叉树 的定义如下:在完全二叉树中,除了最底层节点可能没填满外,其余每层节点数都达到最大值,并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层,则该层包含 1~ 2h 个节点。
- 示例一:
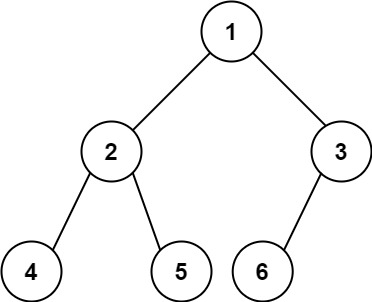
输入:root = [1,2,3,4,5,6]
输出:6
8.2解法一:递归
class Solution {public int countNodes(TreeNode root) {return count(root);}private int count(TreeNode node){if(node==null){return 0;}int leftCount=count(node.left);int rightCount=count(node.right);return leftCount+rightCount+1;}
}
8.3解法二:层序遍历
class Solution {public int countNodes(TreeNode root) {//广度优先遍历Queue<TreeNode> queue=new LinkedList<>();int count=0;if(root==null){return count;}queue.offer(root);while(!queue.isEmpty()){int size=queue.size();count+=size;while(size>0){TreeNode node=queue.poll();if(node.left!=null){queue.offer(node.left);}if(node.right!=null){queue.offer(node.right);}size--;}}return count;}}
9.平衡二叉树
9.1问题
给定一个二叉树,判断它是否是 平衡二叉树
- 示例一:
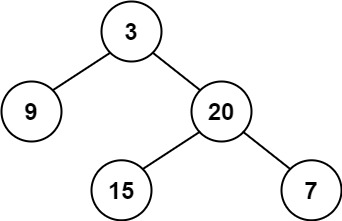
输入:root = [3,9,20,null,null,15,7]
输出:true
9.2解法一:递归
9.2.1递归思路
(1)确定递归函数返回值和参数值
- 题目为确定一棵树是否为平衡树
- 平衡树的定义:一棵树为空或者其左右节点的高度差的绝对值不超过1
- 即递归函数参数为一个树节点,返回值为该节点的高度(注意:若返回-1,则表明该树不平衡)
int isBalancedTree(TreeNode node)
(2)确定终止条件
- 若该节点为null,返回0
if(node==null){return 0;
}
(3)确定递归逻辑
- 传入一个节点,要求返回其高度,即需要求其左、右节点的高度
- 分别求完左、右节点的高度之后,判断其中是否为-1,若为-1,则返回-1,代表不平衡
- 若均不为-1,则求出该节点的平衡因子,若其绝对值超过1,则返回-1,代表不平衡
- 否则返回当前节点为根节点的树的最大高度
int leftHeight=isBalancedTree(node.left);
int rightHeight=isBalancedTree(node.right);
if(leftHeight==-1 || rightHeight==-1){return -1;
}
if(Math.abs(leftHeight-rightHeight)>1){return -1;
}
return 1+Math(leftHeight,rightHeight);
9.2.2代码
class Solution {public boolean isBalanced(TreeNode root) {return isBalancedTree(root)!=-1;}private int isBalancedTree(TreeNode node){if(node==null){return 0;}int leftHeight=isBalancedTree(node.left);int rightHeight=isBalancedTree(node.right);if(leftHeight==-1 || rightHeight==-1){return -1;}if(Math.abs(leftHeight-rightHeight)>1){return -1;}return 1+Math.max(leftHeight,rightHeight);}
}
10.完全二叉树的所有路径
10.1问题
给你一个二叉树的根节点 root ,按 任意顺序 ,返回所有从根节点到叶子节点的路径。
叶子节点 是指没有子节点的节点。
- 示例一:
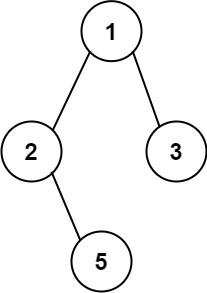
输入:root = [1,2,3,null,5]
输出:["1->2->5","1->3"]
10.2解法一:前序遍历+回溯
- 题目要求从根节点到叶子的路径,所以需要前序遍历,这样才方便让父节点指向孩子节点,找到对应的路径
- 把路径记录下来,需要回溯来回退一个路径再进入另一个路径。
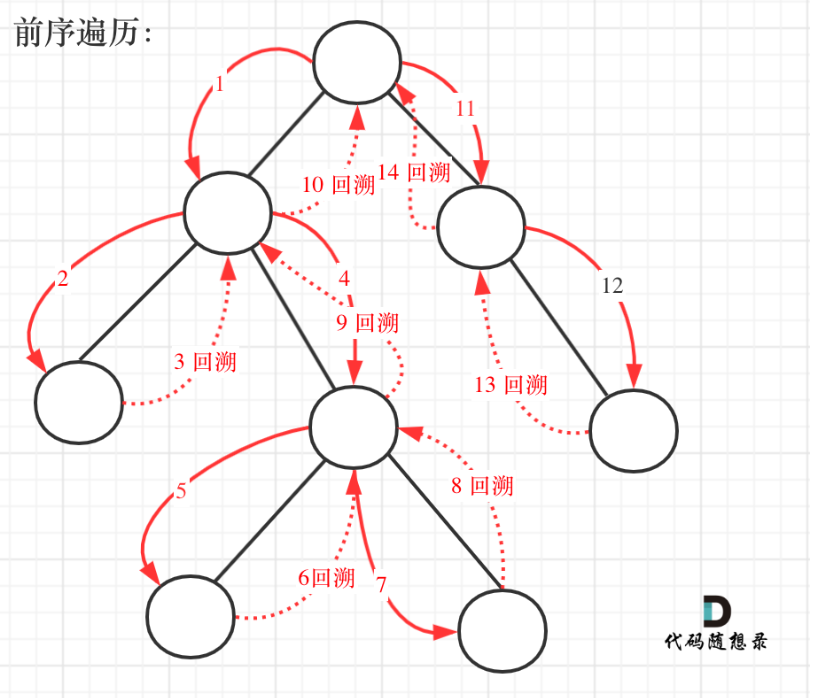
10.2.1递归思路
(1)确定递归函数参数以及返回值
- 求以node为根节点到达叶子节点的路径
- paths存放路径值
- res存放最终结果
void traversal(TreeNode node,List<Integer> paths,List<String> res)
(2)确定递归终止条件
- 当遍历到了叶子节点,即为一条完整的路径
- 取出paths的全部节点,并加入到res中
- 直接return
if(node.left==null && node.right==null){// 输出StringBuilder sb = new StringBuilder();// StringBuilder用来拼接字符串,速度更快for (int i = 0; i < paths.size() - 1; i++) {sb.append(paths.get(i)).append("->");}sb.append(paths.get(paths.size() - 1));// 记录最后一个节点res.add(sb.toString());// 收集一个路径return;
}
(3)确定递归逻辑
// 递归和回溯是同时进行,所以要放在同一个花括号里if (root.left != null) { // 左traversal(root.left, paths, res);paths.remove(paths.size() - 1);// 回溯}if (root.right != null) { // 右traversal(root.right, paths, res);paths.remove(paths.size() - 1);// 回溯}
10.2.2代码实现
class Solution {public List<String> binaryTreePaths(TreeNode root) {List<Integer> paths=new ArrayList<>();List<String> res=new ArrayList<>();traversal(root,paths,res);return res;}private void traversal(TreeNode node,List<Integer> paths,List<String> res){//1、前序遍历(中左右)处理该节点paths.add(node.val);//2、终止条件:该节点为叶子节点if(node.left==null && node.right==null){StringBuilder sb=new StringBuilder();for(int i=0;i<paths.size()-1;i++){sb.append(paths.get(i)).append("->");}//加入最后一个节点sb.append(paths.get(paths.size()-1));res.add(sb.toString());return;}//3、递归逻辑+回溯if(node.left!=null){traversal(node.left,paths,res);//回溯paths.remove(paths.size() - 1); //去除最后一个节点}if(node.right!=null){traversal(node.right,paths,res);//回溯paths.remove(paths.size() - 1); //去除最后一个节点}}
}
