当前位置：首页 > news >正文

算法系列--动态规划--⼦数组、⼦串系列（数组中连续的⼀段）(1)

news 2025/7/18 4:41:57

💕"我们好像在池塘的水底，从一个月亮走向另一个月亮。"💕
作者：Mylvzi
文章主要内容：算法系列–动态规划–⼦数组、⼦串系列（数组中连续的⼀段）(1)

大家好,今天为大家带来的是算法系列--动态规划--⼦数组、⼦串系列（数组中连续的⼀段）(1),这是动态规划新的一种题型

1.最⼤⼦数组和

链接:
https://leetcode.cn/problems/maximum-subarray/
分析:

动态规划的子数组问题和前缀和问题是不一样的,

子数组和这道题要求的是子数组和的最大值,我们的状态表示就是记录以i位置为结束的所有子数组的最大和,而前缀和只是一种快速求出区间和的方法,并没有表示最大和这种状态

关于求最大子数组和问题这道题,要注意状态表示的含义以i位置为结尾的所有子数组的最大和,也就是必须以i位置为结尾,那么此时的状态其实只有两种:

单独一个
前面的一堆 + 它本身

网上的很多推到状态方程的时候其实很容易让人误解,解释的也不清楚,他们进行状态的分类是根据dp[i - 1]的正负来推导dp[i]的,有的人可能想为什么不判断nums[i]的正负呢?

其实本质都一样,笔者觉得单纯通过形式来推到方程更容易理解一些

子串/子数组问题的一个经验的状态分类就是按照长度分类的,因为他们的状态表示都比较固定,都是以i位置为结束的最大xxxx

有的题目还比较恶心(尤其是关于子串的问题),对于相同的子串有时候还需要去重,就需要额外开一个数组来统计次数

本题的分析思路:
在这里插入图片描述

代码:

class Solution {public int maxSubArray(int[] nums) {int n = nums.length;int dp = 0;int max = -0x3f3f3f3f;// 将最大/小值设置为+-ox3f3f3f3f是一种经验for(int num : nums) {dp = Math.max(num,dp + num);// 填表max = Math.max(max,dp);// 更新最值}return max;}
}

2.环形⼦数组的最⼤和

链接:
https://leetcode.cn/problems/maximum-sum-circular-subarray/description/
分析:

本题是上题的一个变种,这里带环了,对于带环的问题,我们最常用的一个做法是想办法将其转化为线性的,对于本题我们可以采用分类讨论的思想

根据什么区分类讨论呢?往往是根据最后结果可能出现的形式去考虑,对于本题,最长的子数组和可能是两种情况

不带环,在区间内部
带环,跨越区间

对于情况1,就是最大子数组和的解法,对于情况2,可以转化为求区间内的最小值,那么最大值就是sum - min,最后返回情况1和情况2的最大值即可

下面是详细分析过程

在这里插入图片描述

代码:

class Solution {public int maxSubarraySumCircular(int[] nums) {// 创建dp表int n = nums.length;if(n == 1) return nums[0];int[] f = new int[n];int[] g = new int[n];// 初始化f[0] = g[0] = nums[0];int max = -0x3f3f3f3f;int min = 0x3f3f3f3f;int sum = nums[0];// 填表for(int i = 1; i < n; i++) {f[i] = Math.max(nums[i],f[i - 1] + nums[i]);g[i] = Math.min(nums[i],g[i - 1] + nums[i]);max = Math.max(max,f[i]);min = Math.min(min,g[i]);sum += nums[i];}// 返回值return sum == min ? max : Math.max(max,sum - min);}
}

3.乘积最⼤⼦数组

链接:
https://leetcode.cn/problems/maximum-product-subarray/
分析:

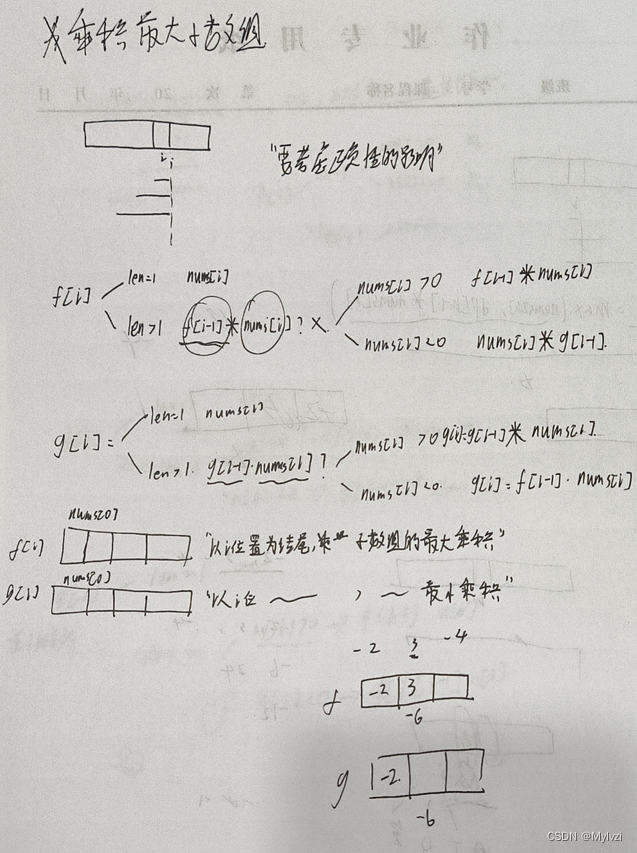
首先想到的状态表示就是以i位置为结尾子数组的最大乘积,但是根据这个状态表示去推到状态转移方程时发现只使用一个dp表无法表示所有的情况

当nums[i] > 0,i位置的状态就是前一个位置的最大乘积 * nums[i]
当nums[i] < 0,此时无法通过dp[i - 1]来推到dp[i],因为一个负数 * 较大的数一定会变小,那么dp[i]存储的就是以i位置为结尾的子数组的最小乘积,这与我们的状态表示是矛盾的

既然当nums[i] < 0时,需要乘的是以i-1位置为结尾的子数组的最小乘积,那么我们就创建出一个dp表g[i]来表示最小乘积,以下是详细分析过程:
在这里插入图片描述

代码:

class Solution {public int maxProduct(int[] nums) {// 创建dp表int n = nums.length;int[] f = new int[n];int[] g = new int[n];// 初始化f[0] = g[0] = nums[0];int max = f[0];// 填表for(int i = 1; i < n; i++) {int t1 = 0, t2 = 0;if(nums[i] > 0) {f[i] = f[i - 1] * nums[i];g[i] = g[i - 1] * nums[i];}else {f[i] = g[i - 1] * nums[i];g[i] = f[i - 1] * nums[i];}f[i] = Math.max(nums[i],f[i]);g[i] = Math.min(nums[i],g[i]);max = Math.max(f[i],max);}return max;}
}

4.乘积为正数的最⻓⼦数组

链接:
https://leetcode.cn/problems/maximum-length-of-subarray-with-positive-product/description/
分析:

本题相较于上题有两个不同:

本题要求乘积必须为正数
本题求解的不是最大的乘积,而是乘积为正数的最长子数组

和上题一样,本题同样需要使用两个dp表来进行状态表示

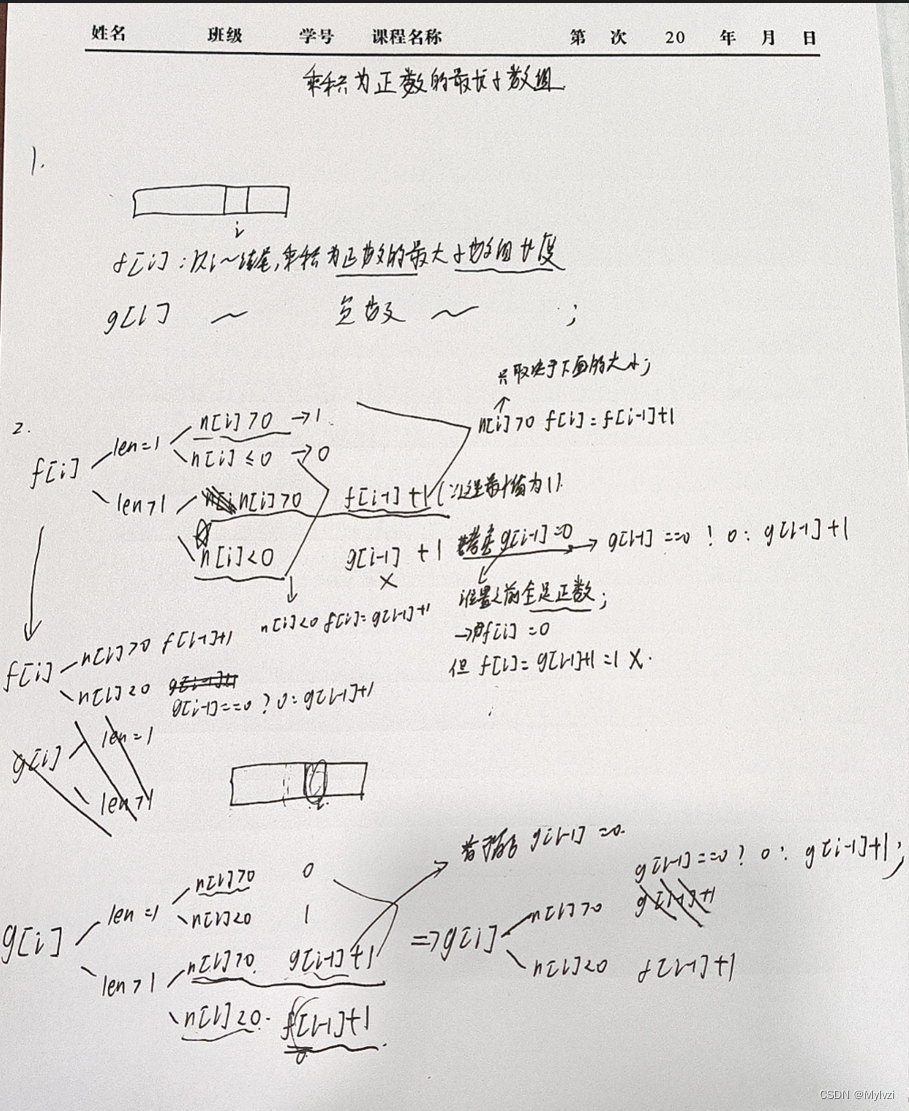
f[i]:以i位置为结尾,乘积为正数的最大子数组长度
g[i]:以i位置为结尾,乘积为负数的最大子数组长度

状态转移方程推导如下:

在这里插入图片描述

注意特殊情况:

当n[i] < 0时,f[i] == g[i - 1] + 1,但是如果i位置之前全是正数,此时g[i - 1] == 0,那么f[i] == 0 + 1 = 1了,但是因为n[i] < 0,i位置的f[i]应该等于 0,因为所有的以i位置为结尾的子数组的乘积必然为负数

代码:

class Solution {public int getMaxLen(int[] nums) {int n = nums.length;// 1.创建dp表int[] f = new int[n];int[] g = new int[n];// 2.根据状态表示进行初始化f[0] = nums[0] > 0 ? 1 : 0;g[0] = nums[0] < 0 ? 1 : 0;int max = -0x3f3f3f3f;// 3.填表for(int i = 1; i < n; i++) {if(nums[i] > 0) {f[i] = f[i - 1] + 1;g[i] = g[i - 1] == 0 ? 0 : g[i - 1] + 1;}else if(nums[i] < 0){f[i] = g[i - 1] == 0 ? 0 : g[i - 1] + 1;g[i] = f[i - 1] + 1;}else {f[i] = g[i] = 0;// 注意等于0相当于直接截断 要重新计数 从0开始}max = Math.max(f[i],max);// 更新长度}// 处理n == 1的情况return max == -0x3f3f3f3f ? f[0] : max;}
}