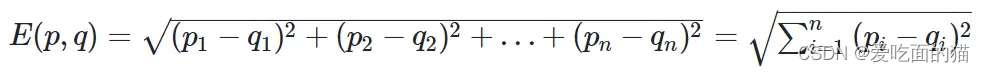常用相似度计算方法总总结
一、欧几里得相似度
1、欧几里得相似度
公式如下所示:
 2、自定义代码实现
2、自定义代码实现
import numpy as np
def EuclideanDistance(x, y):import numpy as npx = np.array(x)y = np.array(y)return np.sqrt(np.sum(np.square(x-y)))# 示例数据
# 用户1 的A B C D E商品数据 [3.3,6.5,2.8,3.4,5.5]
# 用户2 的A B C D E商品数据 [3.5,5.8,3.1,3.6,5.1]
x = np.array([3.3,6.5,2.8,3.4,5.5])
y = np.array([3.5,5.8,3.1,3.6,5.1])euclidean_distance = EuclideanDistance(x, y)
print(f"euclidean distance is: {euclidean_distance}")二、皮尔森相关性系数
1、皮尔森相关性系数
相关系数:考察两个事物(在数据里我们称之为变量)之间的相关程度。
公式如下所示:
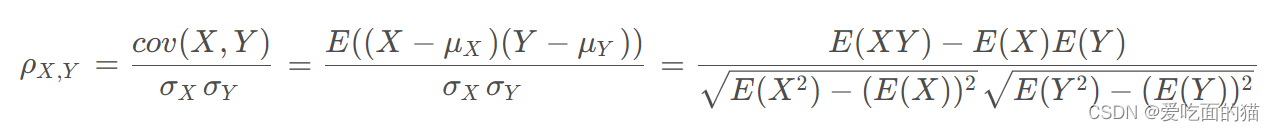

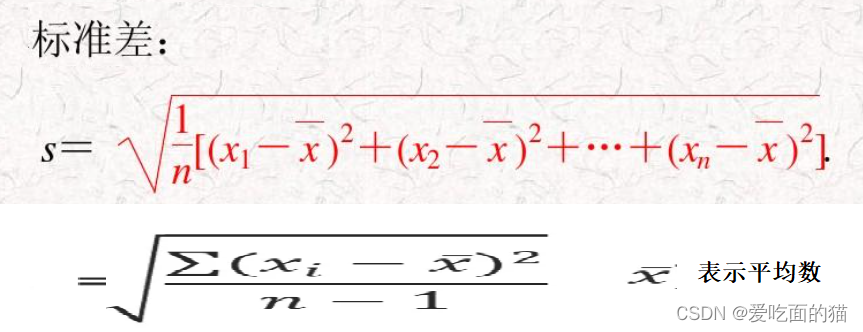
如果有两个变量:X、Y,最终计算出的相关系数的含义可以有如下理解:
(1)、当相关系数为0时,X和Y两变量无关系。
(2)、当X的值增大(减小),Y值增大(减小),两个变量为正相关,相关系数在0.00与1.00之间。
(3)、当X的值增大(减小),Y值减小(增大),两个变量为负相关,相关系数在-1.00与0.00之间。
相关系数的绝对值越大,相关性越强,相关系数越接近于1或-1,相关度越强,相关系数越接近于0,相关度越弱。
通常情况下通过以下取值范围判断变量的相关强度:
相关系数 0.8-1.0 极强相关
0.6-0.8 强相关
0.4-0.6 中等程度相关
0.2-0.4 弱相关
0.0-0.2 极弱相关或无相关
2、代码实现过程
自定义实现过程
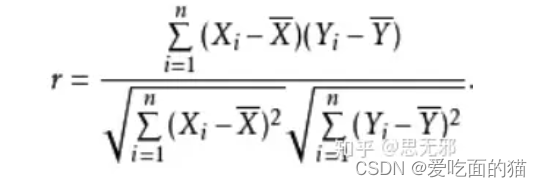
import numpy as npdef pearson_correlation(x, y):n = len(x)# 计算平均值x_bar = np.sum(x) / n
# y_bar = np.sum(y) / n# 计算协方差cov_xy = np.sum((x - x_bar) * (y - y_bar))# 计算标准差std_dev_x = np.sqrt(np.sum((x - x_bar) ** 2) / (n - 1))std_dev_y = np.sqrt(np.sum((y - y_bar) ** 2) / (n - 1))# 计算皮尔逊相似系数r = cov_xy / (std_dev_x * std_dev_y)return r# 示例数据
# 用户1 的A B C D E商品数据 [3.3,6.5,2.8,3.4,5.5]
# 用户2 的A B C D E商品数据 [3.5,5.8,3.1,3.6,5.1]
x = np.array([3.3,6.5,2.8,3.4,5.5])
y = np.array([3.5,5.8,3.1,3.6,5.1])# 计算皮尔逊相似系数
pearson_coefficient = pearson_correlation(x, y)
print(f"Pearson correlation coefficient: {pearson_coefficient}")numpy中的corrcpef()封装实现
import numpy as np# 示例数据
# 用户1 的A B C D E商品数据 [3.3,6.5,2.8,3.4,5.5]
# 用户2 的A B C D E商品数据 [3.5,5.8,3.1,3.6,5.1]x=np.array([3.3,6.5,2.8,3.4,5.5])
y=np.array([3.5,5.8,3.1,3.6,5.1])pc=np.corrcoef(x,y)print(pc)3、适用范围
当两个变量的标准差都不为零时,相关系数才有定义,皮尔逊相关系数适用于:
(1)、两个变量之间是线性关系,都是连续数据。
(2)、两个变量的总体是正态分布,或接近正态的单峰分布。
(3)、两个变量的观测值是成对的,每对观测值之间相互独立。
三、余弦相似度
1、余弦相似度
公式如下所示:
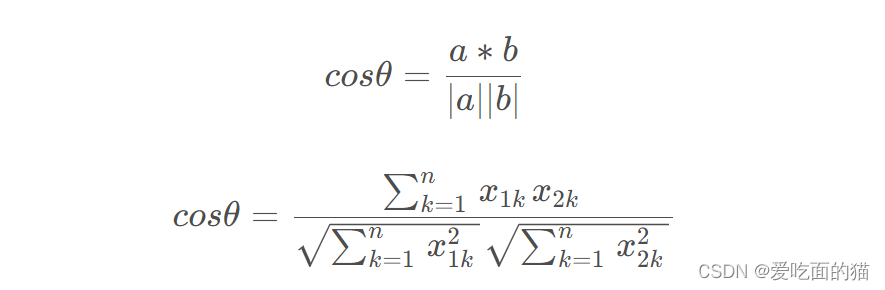
2、自定义代码实现
import numpy as np
def moreCos(a,b):sum_fenzi = 0.0sum_fenmu_1,sum_fenmu_2 = 0,0for i in range(len(a)):sum_fenzi += a[i]*b[i]sum_fenmu_1 += a[i]**2sum_fenmu_2 += b[i]**2return sum_fenzi/(np.sqrt(sum_fenmu_1) * np.sqrt(sum_fenmu_2) )# 示例数据
# 用户1 的A B C D E商品数据 [3.3,6.5,2.8,3.4,5.5]
# 用户2 的A B C D E商品数据 [3.5,5.8,3.1,3.6,5.1]
x = np.array([3.3,6.5,2.8,3.4,5.5])
y = np.array([3.5,5.8,3.1,3.6,5.1])cos = moreCos(x, y)
print(f"cos is: {cos}")四、曼哈顿相似度
1、曼哈顿相似度
公式如下所示:
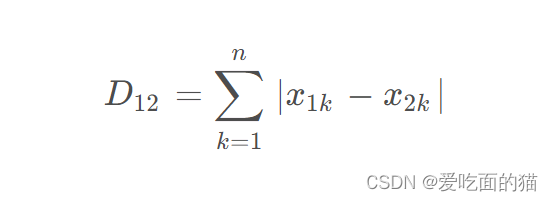
2、自定义代码实现
import numpy as np
def ManhattanDistance(x, y):import numpy as npx = np.array(x)y = np.array(y)return np.sum(np.abs(x-y))# 示例数据
# 用户1 的A B C D E商品数据 [3.3,6.5,2.8,3.4,5.5]
# 用户2 的A B C D E商品数据 [3.5,5.8,3.1,3.6,5.1]
x = np.array([3.3,6.5,2.8,3.4,5.5])
y = np.array([3.5,5.8,3.1,3.6,5.1])manhattan_distance = ManhattanDistance(x, y)
print(f"manhattan distance is: {manhattan_distance}")五、切比雪夫距离
1、切比雪夫距离
公式如下所示:
切比雪夫距离(Chebyshev Distance)的定义为:max( | x2-x1 | , |y2-y1 | , … ), 切比雪夫距离用的时候数据的维度必须是三个以上。
2、自定义代码实现
import numpy as np
def ChebyshevDistance(x, y):import numpy as npx = np.array(x)y = np.array(y)return np.max(np.abs(x-y))# 示例数据
# 用户1 的A B C D E商品数据 [3.3,6.5,2.8,3.4,5.5]
# 用户2 的A B C D E商品数据 [3.5,5.8,3.1,3.6,5.1]
x = np.array([3.3,6.5,2.8,3.4,5.5])
y = np.array([3.5,5.8,3.1,3.6,5.1])chebyshev_istance = ChebyshevDistance(x, y)
print(f"manhattan distance is: {chebyshev_istance}")六、马氏距离
1、马氏距离
公式如下所示:
M个样本向量X1~Xm,协方差矩阵记为S,均值记为向量μ,则其中样本向量X到u的马氏距离表示为
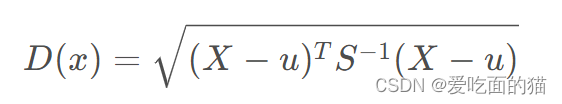
2、自定义代码实现
def MahalanobisDistance(x, y):'''马氏居立中的(x,y)与欧几里得距离的(x,y)不同,欧几里得距离中的(x,y)指2个样本,每个样本的维数为x或y的维数;这里的(x,y)指向量是2维的,样本个数为x或y的维数,若要计算n维变量间的马氏距离则需要改变输入的参数如(x,y,z)为3维变量。'''import numpy as npx = np.array(x)y = np.array(y)X = np.vstack([x, y])X_T = X.Tsigma = np.cov(X)sigma_inverse = np.linalg.inv(sigma)d1 = []for i in range(0, X_T.shape[0]):for j in range(i + 1, X_T.shape[0]):delta = X_T[i] - X_T[j]d = np.sqrt(np.dot(np.dot(delta, sigma_inverse), delta.T))d1.append(d)return d1# 示例数据
# 用户1 的A B C D E商品数据 [3.3,6.5,2.8,3.4,5.5]
# 用户2 的A B C D E商品数据 [3.5,5.8,3.1,3.6,5.1]
x = np.array([3.3,6.5,2.8,3.4,5.5])
y = np.array([3.5,5.8,3.1,3.6,5.1])mahalanobis_istance = MahalanobisDistance(x, y)
print(f"mahalanobis distance is: {mahalanobis_istance}")七、闵可夫斯基距离
1、闵可夫斯基距离
公式如下所示:
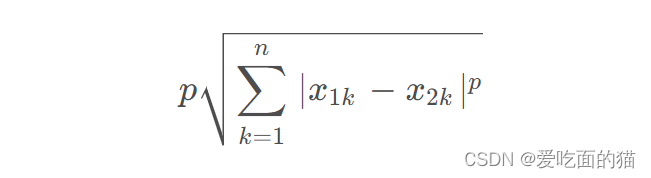
当p=1时,就是曼哈顿距离
当p=2时,就是欧氏距离
当p→∞时,就是切比雪夫距离
2、自定义代码实现
import numpy as npdef MinkowskiDistance(x, y, p):import mathimport numpy as npzipped_coordinate = zip(x, y)return math.pow(np.sum([math.pow(np.abs(i[0] - i[1]), p) for i in zipped_coordinate]), 1 / p)# 示例数据
# 用户1 的A B C D E商品数据 [3.3,6.5,2.8,3.4,5.5]
# 用户2 的A B C D E商品数据 [3.5,5.8,3.1,3.6,5.1]
x = np.array([3.3, 6.5, 2.8, 3.4, 5.5])
y = np.array([3.5, 5.8, 3.1, 3.6, 5.1])# minkowski_istance = MinkowskiDistance(x, y,1)
# minkowski_istance = MinkowskiDistance(x, y,2)
minkowski_istance = MinkowskiDistance(x, y,3)
print(f"minkowski_ distance is: {minkowski_istance}")
八、信息熵
1、 信息熵
衡量分布的混乱程度或分散程度的一种度量.
熵的值就越大,样本一致性越低,越代表分之样本种类越多,越混乱,不确定性越强。
熵的值就越小,样本一致性越高,样本越倾向于某一类。
熵的值就为0,代表样本完全属于同一类。
公式如下所示:
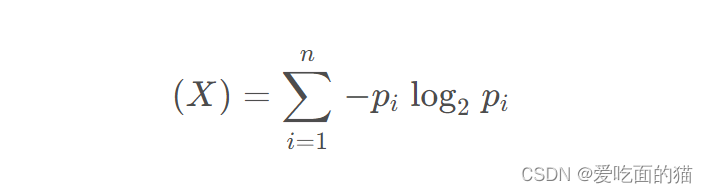
2、自定义代码实现
import numpy as np# 示例数据data=np.array(['a','b','c','a','a','b'])data1=np.array(['中国','中国','中国','中国','中国','中国','中国','中国','人民',])#计算信息熵的方法
def calc_ent(x):"""calculate shanno ent of x"""x_value_list = set([x[i] for i in range(x.shape[0])])ent = 0.0for x_value in x_value_list:p = float(x[x == x_value].shape[0]) / x.shape[0]logp = np.log2(p)ent -= p * logpreturn entent = calc_ent(data)
ent1= calc_ent(data1)print(f"ent is: {ent}")
print(f"ent is: {ent1}")