蓝桥杯练习题——dp
五部曲(代码随想录)
1.确定 dp 数组以及下标含义
2.确定递推公式
3.确定 dp 数组初始化
4.确定遍历顺序
5.debug
入门题
1.斐波那契数

思路
1.f[i]:第 i 个数的值
2.f[i] = f[i - 1] + f[i - 2]
3.f[0] = 0, f[1] = 1
4.顺序遍历
5.记得特判 n == 0 的时候,因为初始化了 f[1]
class Solution {
public:int fib(int n) {if(n == 0) return n;vector<int> f(n + 1);f[0] = 0, f[1] = 1;for(int i = 2; i <= n; i++) f[i] = f[i - 1] + f[i - 2];return f[n];}
};
2.爬楼梯

思路
每次可以从下面一个台阶或者下面两个台阶处上来
1.f[i]:爬到第 i 阶楼梯有多少种方法
2.f[i] = f[i - 1] + f[i - 2]
3.f[0] = 1, f[1] = 1
4.顺序遍历
class Solution {
public:int climbStairs(int n) {vector<int> f(n + 1);f[0] = 1, f[1] = 1;for(int i = 2; i <= n; i++) f[i] = f[i - 1] + f[i - 2];return f[n];}
};
3.使用最小花费爬楼梯

思路
可以从 0 或 1 处开始爬楼梯,需要爬到第 n 阶楼梯
1.f[i]:爬到第 i 阶楼梯需要的最小花费
2.f[i] = min(f[i - 1] + cost[i - 1], f[i - 2] + cost[i - 2)
3.f[0] = 0, f[1] = 0
4.顺序遍历
class Solution {
public:int minCostClimbingStairs(vector<int>& cost) {int n = cost.size();vector<int> f(n + 1);f[0] = 0, f[1] = 0;for(int i = 2; i <= n; i++){f[i] = min(f[i - 1] + cost[i - 1], f[i - 2] + cost[i - 2]);}return f[n];}
};
4.不同路径

思路
1.f[i][j]: 走到 (i, j) 总共的路径
2.f[i][j] = f[i - 1][j] + f[i][j - 1]
3.f[i][1] = 1, f[1][i] = 1
4.顺序遍历
class Solution {
public:int uniquePaths(int m, int n) {vector<vector<int>> f(n + 1, vector<int>(m + 1));for(int i = 0; i <= n; i++) f[i][1] = 1;for(int i = 0; i <= m; i++) f[1][i] = 1;for(int i = 2; i <= n; i++){for(int j = 2; j <= m; j++){f[i][j] = f[i - 1][j] + f[i][j - 1];}}return f[n][m];}
};
5.不同路径 II
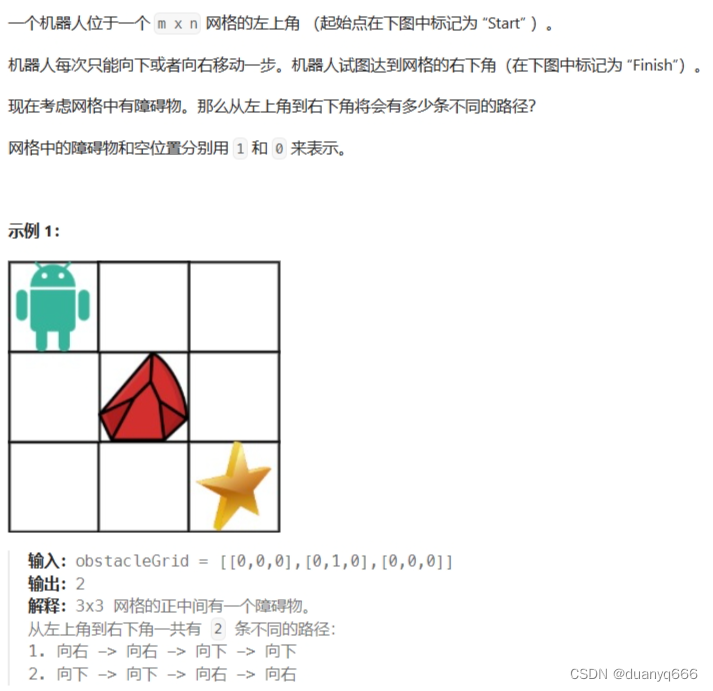
思路
1.f[i][j]: 走到 (i, j) 总共的路径
2.f[i][j] = f[i - 1][j] + f[i][j - 1]
3.f[i][0] = 1, f[0][i] = 1, 其他 = 0
4.顺序遍历
class Solution {
public:int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {int n = obstacleGrid.size();int m = obstacleGrid[0].size();vector<vector<int>> f(n, vector<int>(m, 0));for(int i = 0; i < n && !obstacleGrid[i][0]; i++) f[i][0] = 1;for(int i = 0; i < m && !obstacleGrid[0][i]; i++) f[0][i] = 1;for(int i = 1; i < n; i++){for(int j = 1; j < m; j++){if(!obstacleGrid[i][j]){f[i][j] = f[i - 1][j] + f[i][j - 1];}}}return f[n - 1][m - 1];}
};
6.整数拆分

思路
1.f[i]: 拆数字 i 可得到的最大乘积
2.拆分成 j * (i - j) 或 j * f[i - j],f[i] = max(f[i], max(j * (i - j), j * [i - j]))
3.f[0] = 0, f[1] = 1
4.顺序遍历
class Solution {
public:int integerBreak(int n) {vector<int> f(n + 1);f[0] = 0, f[1] = 1;for(int i = 2; i <= n; i++){for(int j = 0; j < i; j++){f[i] = max(f[i], max(j * (i - j), j * f[i - j]));}}return f[n];}
};
7.不同的二叉搜索树
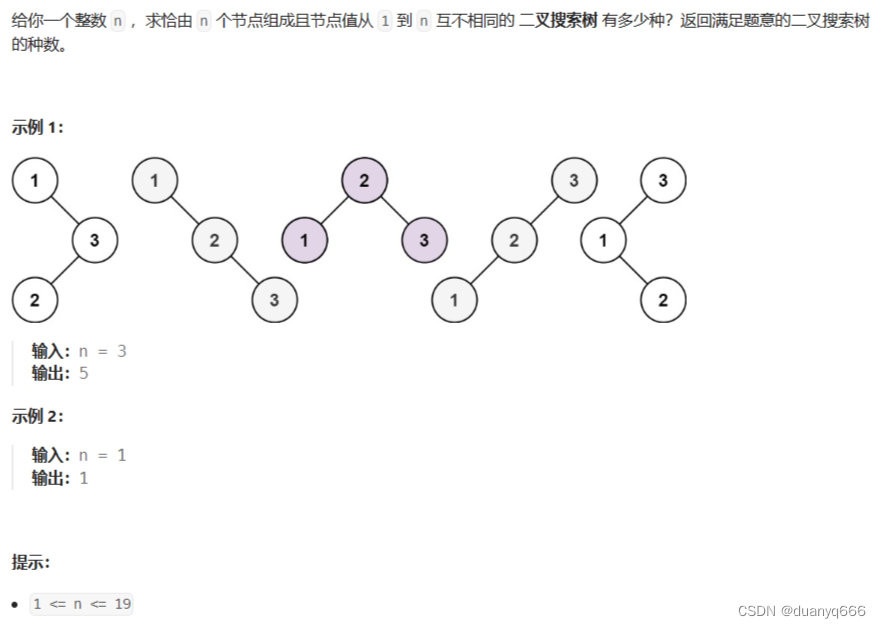
思路
dp[3],就是 元素1为头结点搜索树的数量 + 元素2为头结点搜索树的数量 + 元素3为头结点搜索树的数量
元素1为头结点搜索树的数量 = 右子树有2个元素的搜索树数量 * 左子树有0个元素的搜索树数量
元素2为头结点搜索树的数量 = 右子树有1个元素的搜索树数量 * 左子树有1个元素的搜索树数量
元素3为头结点搜索树的数量 = 右子树有0个元素的搜索树数量 * 左子树有2个元素的搜索树数量
有2个元素的搜索树数量就是dp[2]。
有1个元素的搜索树数量就是dp[1]。
有0个元素的搜索树数量就是dp[0]。
所以dp[3] = dp[2] * dp[0] + dp[1] * dp[1] + dp[0] * dp[2]
dp[i] += dp[以j为头结点左子树节点数量] * dp[以j为头结点右子树节点数量]
1.f[i]: 由 1 到 i 个节点的二叉搜索树个数
2.f[i] += f[j - 1] * f[i - j]
3.f[0] = 1
4.顺序遍历
class Solution {
public:int numTrees(int n) {vector<int> f(n + 1);f[0] = 1;for(int i = 1; i <= n; i++){for(int j = 1; j <= i; j++){f[i] += f[j - 1] * f[i - j];}}return f[n];}
};
背包问题
1.01背包问题

思路
1.f[i][j]: 前 i 个物品在容量为 j 的情况下的最大价值
2.f[i][j] = max(f[i - 1][j], f[i - 1][j - v[i]] + w[i])
3.全部 = 0
4.顺序遍历
#include<iostream>
using namespace std;
const int N = 1e3 + 10;
int f[N][N], v[N], w[N];
int n, m;int main(){scanf("%d%d", &n, &m);for(int i = 1; i <= n; i++) scanf("%d%d", &v[i], &w[i]);for(int i = 1; i <= n; i++){for(int j = 0; j <= m; j++){// 不选f[i][j] = f[i - 1][j];// 选if(v[i] <= j) f[i][j] = max(f[i - 1][j], f[i - 1][j - v[i]] + w[i]);}}printf("%d", f[n][m]);return 0;
}// 滚动数组优化
#include<iostream>
using namespace std;
const int N = 1e3 + 10;
int f[N], v[N], w[N];
int n, m;int main(){scanf("%d%d", &n, &m);for(int i = 1; i <= n; i++) scanf("%d%d", &v[i], &w[i]);for(int i = 1; i <= n; i++){for(int j = m; j >= v[i]; j--){f[j] = max(f[j], f[j - v[i]] + w[i]);}}printf("%d", f[m]);return 0;
}
2.分割等和子集

思路
分割成两个等和子集,即找到是否存在和为 sum / 2 的子集,转化为 01 背包,背包容量为 sum / 2
1.f[j]: 背包容量为 i,放入物品后的最大重量
2.f[j] = max(f[j], f[j - nums[i]] + nums[i])
3.全部 = 0
4.倒序遍历
class Solution {
public:bool canPartition(vector<int>& nums) {int n = nums.size(), sum = 0;for(int i = 0; i < n; i++) sum += nums[i];if(sum % 2) return false;vector<int> f(10001, 0);for(int i = 0; i < n; i++){for(int j = sum / 2; j >= nums[i]; j--){f[j] = max(f[j], f[j - nums[i]] + nums[i]);if(f[j] == sum / 2) return true;}}return false;}
};
3.最后一块石头的重量 II

思路
尽可能分成两堆重量相同,使得相撞后重量最小
1.f[j]: 容量为 j 的背包,最大价值
2.f[j] = max(f[j], f[j - stones[i]] + stones[i])
3.全部 = 0
4.倒序遍历
class Solution {
public:int lastStoneWeightII(vector<int>& stones) {int n = stones.size(), sum = 0;for(int i = 0; i < n; i++) sum += stones[i];vector<int> f(1501, 0);for(int i = 0; i < n; i++){for(int j = sum / 2; j >= stones[i]; j--){f[j] = max(f[j], f[j - stones[i]] + stones[i]);}}return (sum - f[sum / 2]) - f[sum / 2];}
};
4.目标和

思路
pos - neg = tar 得 pos - (sum - pos) = tar 得 pos = (sum + tar) / 2
转换为背包容量为 pos,有多少种情况装满
无解的情况:pos 为奇数,tar 的绝对值大于 sum
只要搞到 nums[i],凑成 f[j] 就有 f[j - nums[i]] 种方法。
例如:f[j],j 为5,
已经有一个1(nums[i])的话,有 f[4]种方法 凑成 容量为5的背包。
已经有一个2(nums[i])的话,有 f[3]种方法 凑成 容量为5的背包。
已经有一个3(nums[i])的话,有 f[2]中方法 凑成 容量为5的背包
已经有一个4(nums[i])的话,有 f[1]中方法 凑成 容量为5的背包
已经有一个5(nums[i])的话,有 f[0]中方法 凑成 容量为5的背包
那么凑整 f[5] 有多少方法呢,也就是把 所有的 f[j - nums[i]] 累加起来。
1.f[j]:填满 j 背包有多少种情况
2.f[j] += f[j - nums[i]]
3.f[0] = 1,其他 = 0
4.倒序遍历
class Solution {
public:int findTargetSumWays(vector<int>& nums, int target) {int n = nums.size(), sum = 0;for(int i = 0; i < n; i++) sum += nums[i];if((sum + target) % 2 || abs(target) > sum) return 0;int pos = (sum + target) / 2;vector<int> f(pos + 1, 0);f[0] = 1;for(int i = 0; i < n; i++){for(int j = pos; j >= nums[i]; j--){f[j] += f[j - nums[i]];}}return f[pos];}
};
5.一和零

思路
可以等价为两个 01 背包,一个装 0,一个装 1
1.f[i][j]: 最多有 i 个 0 和 j 个 1 的最长子集大小
2.f[i][j] = max(f[i][j], f[i - zero][j - one] + 1)
3.全部 = 0
4.倒序遍历
class Solution {
public:int findMaxForm(vector<string>& strs, int m, int n) {vector<vector<int>> f(m + 1, vector<int>(n + 1, 0));for(auto str : strs){int zero = 0, one = 0;for(int i = 0; i < str.size(); i++){if(str[i] == '0') zero++;else one++; }for(int i = m; i >= zero; i--){for(int j = n; j >= one; j--){f[i][j] = max(f[i][j], f[i - zero][j - one] + 1);}}}return f[m][n];}
};
